Jayson Lynch
Michael Pokorny
Meek Models Shall Inherit the Earth
Jul 10, 2025Abstract:The past decade has seen incredible scaling of AI systems by a few companies, leading to inequality in AI model performance. This paper argues that, contrary to prevailing intuition, the diminishing returns to compute scaling will lead to a convergence of AI model capabilities. In other words, meek models (those with limited computation budget) shall inherit the earth, approaching the performance level of the best models overall. We develop a model illustrating that under a fixed-distribution next-token objective, the marginal capability returns to raw compute shrink substantially. Given current scaling practices, we argue that these diminishing returns are strong enough that even companies that can scale their models exponentially faster than other organizations will eventually have little advantage in capabilities. As part of our argument, we give several reasons that proxies like training loss differences capture important capability measures using evidence from benchmark data and theoretical performance models. In addition, we analyze empirical data on the capability difference of AI models over time. Finally, in light of the increasing ability of meek models, we argue that AI strategy and policy require reexamination, and we outline the areas this shift will affect.
EnigmaEval: A Benchmark of Long Multimodal Reasoning Challenges
Feb 13, 2025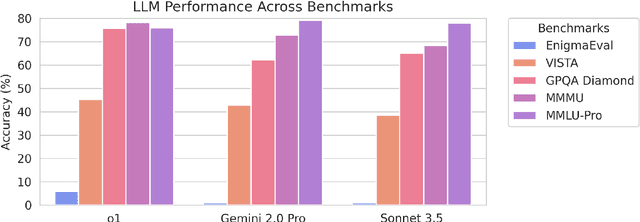



Abstract:As language models master existing reasoning benchmarks, we need new challenges to evaluate their cognitive frontiers. Puzzle-solving events are rich repositories of challenging multimodal problems that test a wide range of advanced reasoning and knowledge capabilities, making them a unique testbed for evaluating frontier language models. We introduce EnigmaEval, a dataset of problems and solutions derived from puzzle competitions and events that probes models' ability to perform implicit knowledge synthesis and multi-step deductive reasoning. Unlike existing reasoning and knowledge benchmarks, puzzle solving challenges models to discover hidden connections between seemingly unrelated pieces of information to uncover solution paths. The benchmark comprises 1184 puzzles of varying complexity -- each typically requiring teams of skilled solvers hours to days to complete -- with unambiguous, verifiable solutions that enable efficient evaluation. State-of-the-art language models achieve extremely low accuracy on these puzzles, even lower than other difficult benchmarks such as Humanity's Last Exam, unveiling models' shortcomings when challenged with problems requiring unstructured and lateral reasoning.
Humanity's Last Exam
Jan 24, 2025Abstract:Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.
A Neural Network Solves and Generates Mathematics Problems by Program Synthesis: Calculus, Differential Equations, Linear Algebra, and More
Jan 04, 2022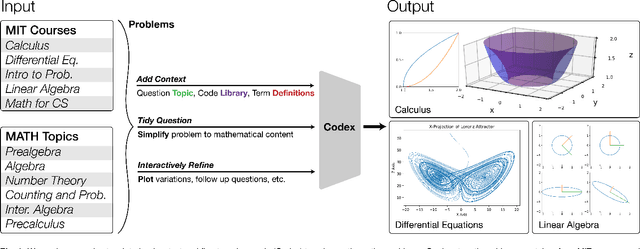
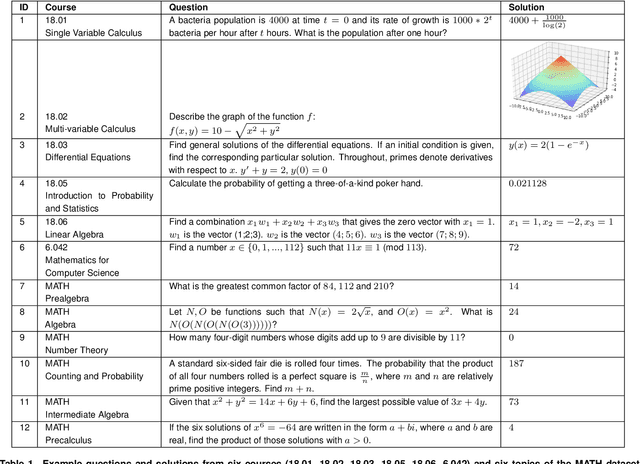
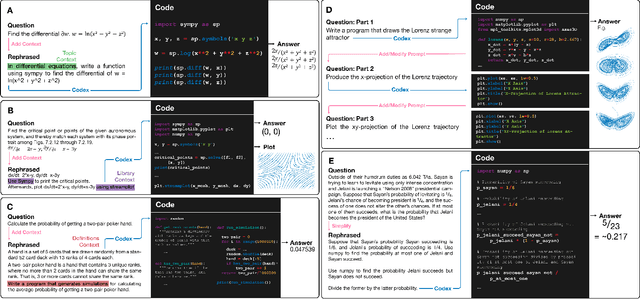
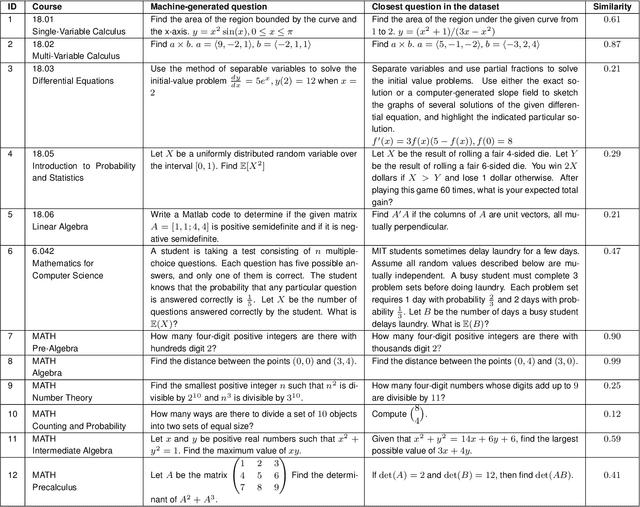
Abstract:We demonstrate that a neural network pre-trained on text and fine-tuned on code solves Mathematics problems by program synthesis. We turn questions into programming tasks, automatically generate programs, and then execute them, perfectly solving university-level problems from MIT's large Mathematics courses (Single Variable Calculus 18.01, Multivariable Calculus 18.02, Differential Equations 18.03, Introduction to Probability and Statistics 18.05, Linear Algebra 18.06, and Mathematics for Computer Science 6.042), Columbia University's COMS3251 Computational Linear Algebra course, as well as questions from a MATH dataset (on Prealgebra, Algebra, Counting and Probability, Number Theory, and Precalculus), the latest benchmark of advanced mathematics problems specifically designed to assess mathematical reasoning. We explore prompt generation methods that enable Transformers to generate question solving programs for these subjects, including solutions with plots. We generate correct answers for a random sample of questions in each topic. We quantify the gap between the original and transformed questions and perform a survey to evaluate the quality and difficulty of generated questions. This is the first work to automatically solve, grade, and generate university-level Mathematics course questions at scale. This represents a milestone for higher education.
Multidimensional Scaling: Approximation and Complexity
Sep 23, 2021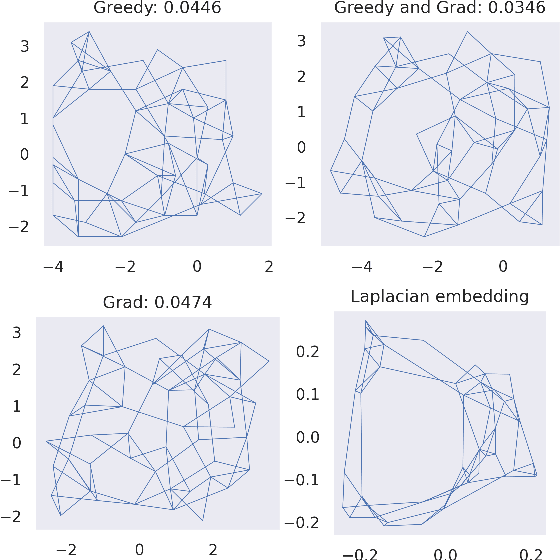

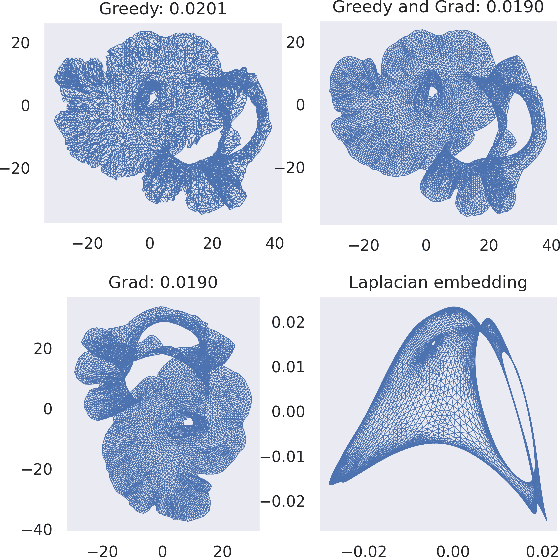
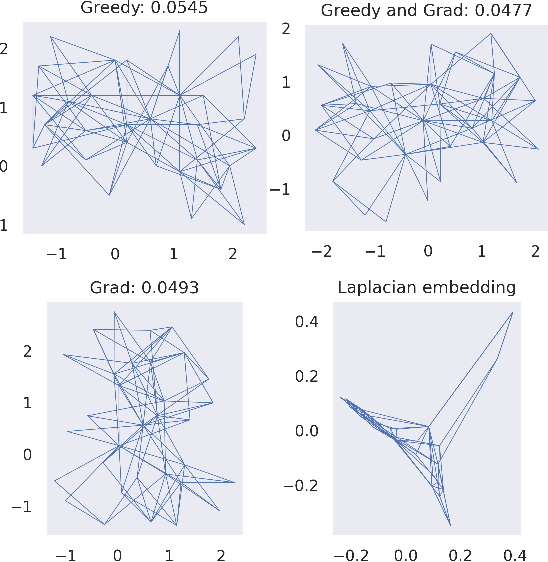
Abstract:Metric Multidimensional scaling (MDS) is a classical method for generating meaningful (non-linear) low-dimensional embeddings of high-dimensional data. MDS has a long history in the statistics, machine learning, and graph drawing communities. In particular, the Kamada-Kawai force-directed graph drawing method is equivalent to MDS and is one of the most popular ways in practice to embed graphs into low dimensions. Despite its ubiquity, our theoretical understanding of MDS remains limited as its objective function is highly non-convex. In this paper, we prove that minimizing the Kamada-Kawai objective is NP-hard and give a provable approximation algorithm for optimizing it, which in particular is a PTAS on low-diameter graphs. We supplement this result with experiments suggesting possible connections between our greedy approximation algorithm and gradient-based methods.
Solving Machine Learning Problems
Jul 02, 2021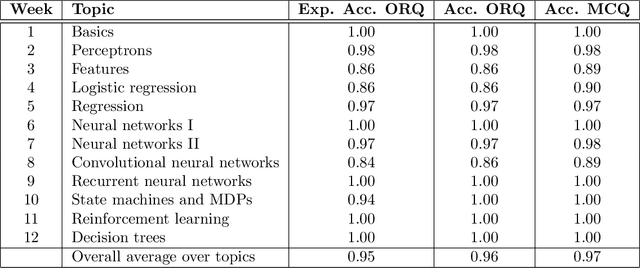

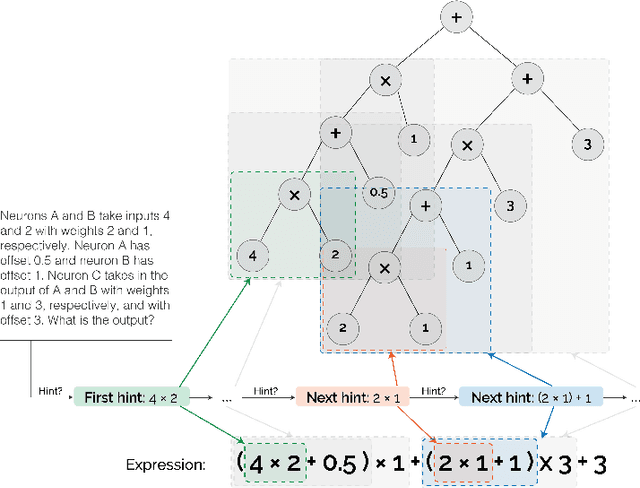
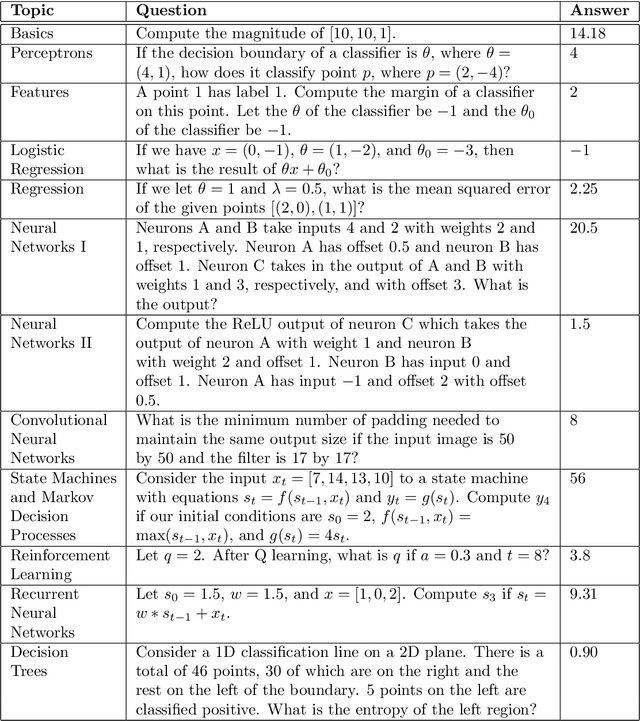
Abstract:Can a machine learn Machine Learning? This work trains a machine learning model to solve machine learning problems from a University undergraduate level course. We generate a new training set of questions and answers consisting of course exercises, homework, and quiz questions from MIT's 6.036 Introduction to Machine Learning course and train a machine learning model to answer these questions. Our system demonstrates an overall accuracy of 96% for open-response questions and 97% for multiple-choice questions, compared with MIT students' average of 93%, achieving grade A performance in the course, all in real-time. Questions cover all 12 topics taught in the course, excluding coding questions or questions with images. Topics include: (i) basic machine learning principles; (ii) perceptrons; (iii) feature extraction and selection; (iv) logistic regression; (v) regression; (vi) neural networks; (vii) advanced neural networks; (viii) convolutional neural networks; (ix) recurrent neural networks; (x) state machines and MDPs; (xi) reinforcement learning; and (xii) decision trees. Our system uses Transformer models within an encoder-decoder architecture with graph and tree representations. An important aspect of our approach is a data-augmentation scheme for generating new example problems. We also train a machine learning model to generate problem hints. Thus, our system automatically generates new questions across topics, answers both open-response questions and multiple-choice questions, classifies problems, and generates problem hints, pushing the envelope of AI for STEM education.
Characterizing Universal Reconfigurability of Modular Pivoting Robots
Dec 14, 2020

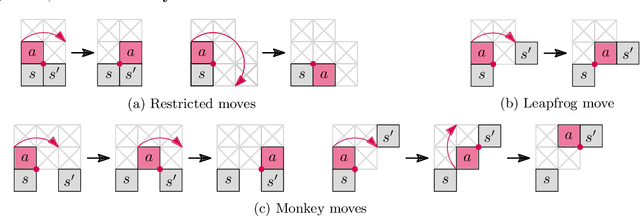

Abstract:We give both efficient algorithms and hardness results for reconfiguring between two connected configurations of modules in the hexagonal grid. The reconfiguration moves that we consider are "pivots", where a hexagonal module rotates around a vertex shared with another module. Following prior work on modular robots, we define two natural sets of hexagon pivoting moves of increasing power: restricted and monkey moves. When we allow both moves, we present the first universal reconfiguration algorithm, which transforms between any two connected configurations using $O(n^3)$ monkey moves. This result strongly contrasts the analogous problem for squares, where there are rigid examples that do not have a single pivoting move preserving connectivity. On the other hand, if we only allow restricted moves, we prove that the reconfiguration problem becomes PSPACE-complete. Moreover, we show that, in contrast to hexagons, the reconfiguration problem for pivoting squares is PSPACE-complete regardless of the set of pivoting moves allowed. In the process, we strengthen the reduction framework of Demaine et al. [FUN'18] that we consider of independent interest.
Walking through Doors is Hard, even without Staircases: Proving PSPACE-hardness via Planar Assemblies of Door Gadgets
Jun 01, 2020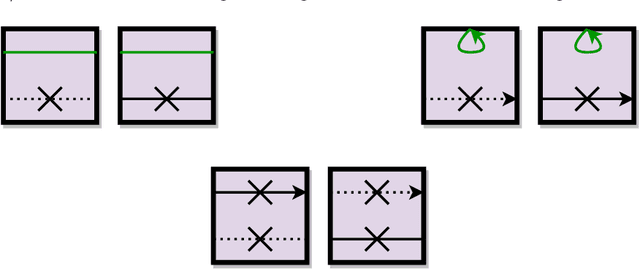
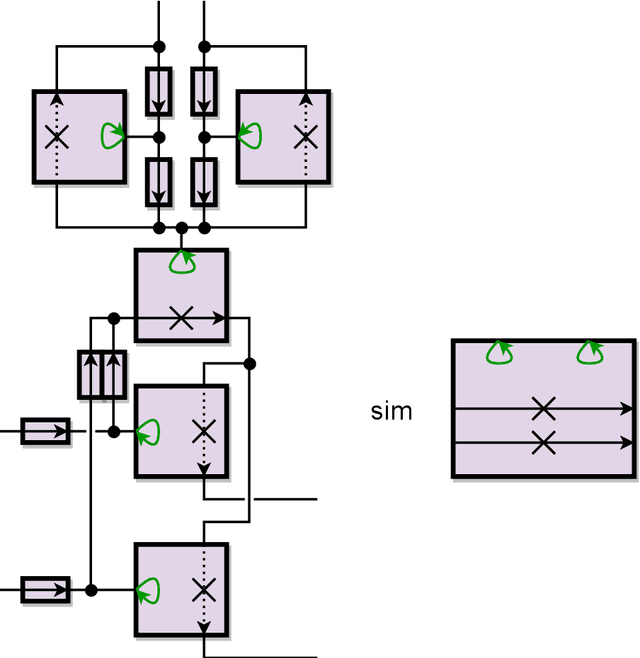
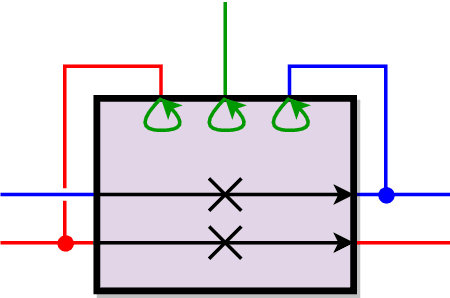
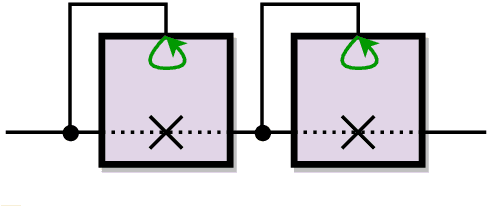
Abstract:A door gadget has two states and three tunnels that can be traversed by an agent (player, robot, etc.): the "open" and "close" tunnel sets the gadget's state to open and closed, respectively, while the "traverse" tunnel can be traversed if and only if the door is in the open state. We prove that it is PSPACE-complete to decide whether an agent can move from one location to another through a planar assembly of such door gadgets, removing the traditional need for crossover gadgets and thereby simplifying past PSPACE-hardness proofs of Lemmings and Nintendo games Super Mario Bros., Legend of Zelda, and Donkey Kong Country. Our result holds in all but one of the possible local planar embedding of the open, close, and traverse tunnels within a door gadget; in the one remaining case, we prove NP-hardness. We also introduce and analyze a simpler type of door gadget, called the self-closing door. This gadget has two states and only two tunnels, similar to the "open" and "traverse" tunnels of doors, except that traversing the traverse tunnel also closes the door. In a variant called the symmetric self-closing door, the "open" tunnel can be traversed if and only if the door is closed. We prove that it is PSPACE-complete to decide whether an agent can move from one location to another through a planar assembly of either type of self-closing door. Then we apply this framework to prove new PSPACE-hardness results for eight different 3D Mario games and Sokobond.
Recursed is not Recursive: A Jarring Result
Feb 12, 2020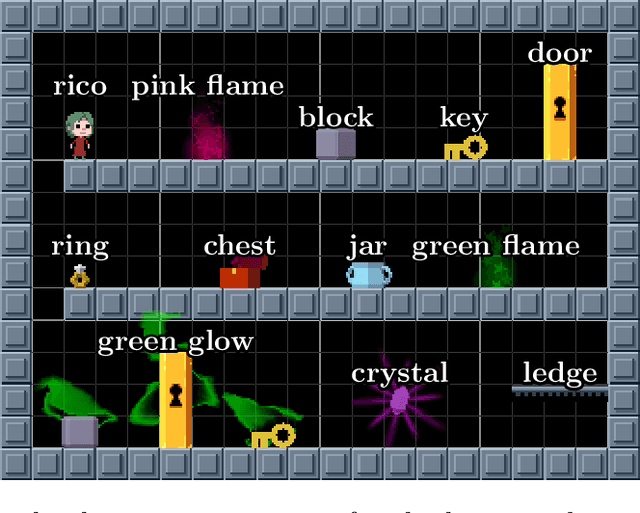
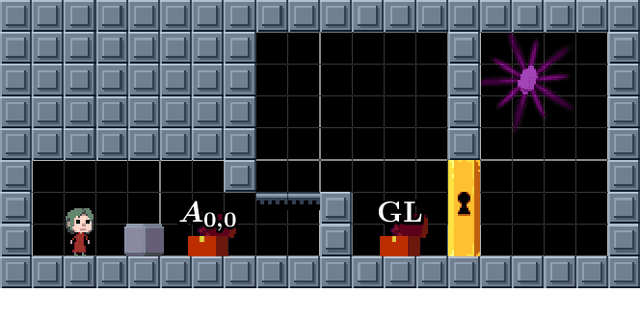

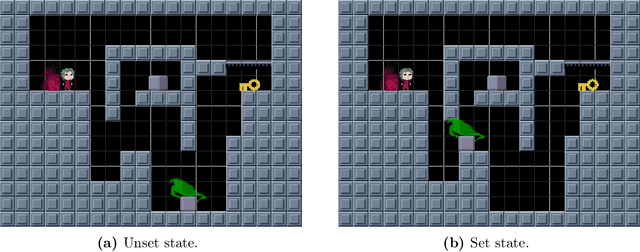
Abstract:Recursed is a 2D puzzle platform video game featuring treasure chests that, when jumped into, instantiate a room that can later be exited (similar to function calls), optionally generating a \jar that returns back to that room (similar to continuations). We prove that Recursed is RE-complete and thus undecidable (not recursive) by a reduction from the Post Correspondence Problem. Our reduction is "practical": the reduction from PCP results in fully playable levels that abide by all constraints governing levels (including the 15x20 room size) designed for the main game. Our reduction is also "efficient": a Turing machine can be simulated by a Recursed level whose size is linear in the encoding size of the Turing machine and whose solution length is polynomial in the running time of the Turing machine.
Computational Complexity of Motion Planning of a Robot through Simple Gadgets
Jun 09, 2018
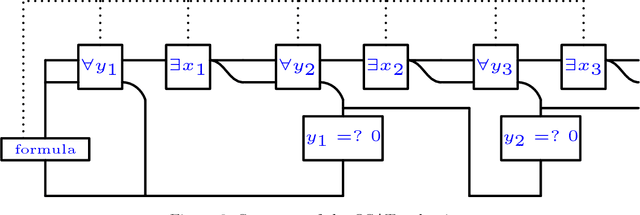
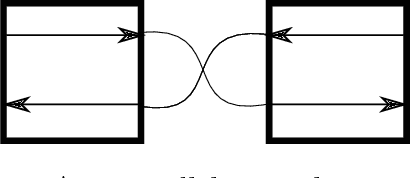
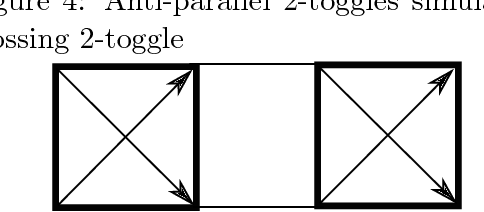
Abstract:We initiate a general theory for analyzing the complexity of motion planning of a single robot through a graph of "gadgets", each with their own state, set of locations, and allowed traversals between locations that can depend on and change the state. This type of setup is common to many robot motion planning hardness proofs. We characterize the complexity for a natural simple case: each gadget connects up to four locations in a perfect matching (but each direction can be traversable or not in the current state), has one or two states, every gadget traversal is immediately undoable, and that gadget locations are connected by an always-traversable forest, possibly restricted to avoid crossings in the plane. Specifically, we show that any single nontrivial four-location two-state gadget type is enough for motion planning to become PSPACE-complete, while any set of simpler gadgets (effectively two-location or one-state) has a polynomial-time motion planning algorithm. As a sample application, our results show that motion planning games with "spinners" are PSPACE-complete, establishing a new hard aspect of Zelda: Oracle of Seasons.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge