Performance of NPG in Countable State-Space Average-Cost RL

We consider policy optimization methods in reinforcement learning settings where the state space is arbitrarily large, or even countably infinite. The motivation arises from control problems in communication networks, matching markets, and other queueing systems. We consider Natural Policy Gradient (NPG), which is a popular algorithm for finite state spaces. Under reasonable assumptions, we derive a performance bound for NPG that is independent of the size of the state space, provided the error in policy evaluation is within a factor of the true value function. We obtain this result by establishing new policy-independent bounds on the solution to Poisson's equation, i.e., the relative value function, and by combining these bounds with previously known connections between MDPs and learning from experts.

Convergence for Natural Policy Gradient on Infinite-State Average-Reward Markov Decision Processes

Infinite-state Markov Decision Processes (MDPs) are essential in modeling and optimizing a wide variety of engineering problems. In the reinforcement learning (RL) context, a variety of algorithms have been developed to learn and optimize these MDPs. At the heart of many popular policy-gradient based learning algorithms, such as natural actor-critic, TRPO, and PPO, lies the Natural Policy Gradient (NPG) algorithm. Convergence results for these RL algorithms rest on convergence results for the NPG algorithm. However, all existing results on the convergence of the NPG algorithm are limited to finite-state settings. We prove the first convergence rate bound for the NPG algorithm for infinite-state average-reward MDPs, proving a $O(1/\sqrt{T})$ convergence rate, if the NPG algorithm is initialized with a good initial policy. Moreover, we show that in the context of a large class of queueing MDPs, the MaxWeight policy suffices to satisfy our initial-policy requirement and achieve a $O(1/\sqrt{T})$ convergence rate. Key to our result are state-dependent bounds on the relative value function achieved by the iterate policies of the NPG algorithm.

Computational Complexity of Motion Planning of a Robot through Simple Gadgets

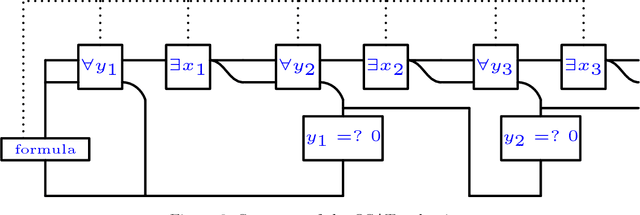
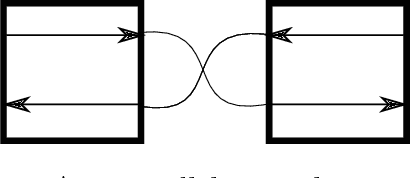
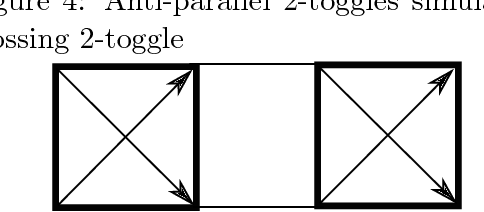
We initiate a general theory for analyzing the complexity of motion planning of a single robot through a graph of "gadgets", each with their own state, set of locations, and allowed traversals between locations that can depend on and change the state. This type of setup is common to many robot motion planning hardness proofs. We characterize the complexity for a natural simple case: each gadget connects up to four locations in a perfect matching (but each direction can be traversable or not in the current state), has one or two states, every gadget traversal is immediately undoable, and that gadget locations are connected by an always-traversable forest, possibly restricted to avoid crossings in the plane. Specifically, we show that any single nontrivial four-location two-state gadget type is enough for motion planning to become PSPACE-complete, while any set of simpler gadgets (effectively two-location or one-state) has a polynomial-time motion planning algorithm. As a sample application, our results show that motion planning games with "spinners" are PSPACE-complete, establishing a new hard aspect of Zelda: Oracle of Seasons.