Finite-Time Bounds for Distributionally Robust TD Learning with Linear Function Approximation

Distributionally robust reinforcement learning (DRRL) focuses on designing policies that achieve good performance under model uncertainties. In particular, we are interested in maximizing the worst-case long-term discounted reward, where the data for RL comes from a nominal model while the deployed environment can deviate from the nominal model within a prescribed uncertainty set. Existing convergence guarantees for robust temporal-difference (TD) learning for policy evaluation are limited to tabular MDPs or are dependent on restrictive discount-factor assumptions when function approximation is used. We present the first robust TD learning with linear function approximation, where robustness is measured with respect to the total-variation distance and Wasserstein-l distance uncertainty set. Additionally, our algorithm is both model-free and does not require generative access to the MDP. Our algorithm combines a two-time-scale stochastic-approximation update with an outer-loop target-network update. We establish an $\tilde{O}(1/\epsilon^2)$ sample complexity to obtain an $\epsilon$-accurate value estimate. Our results close a key gap between the empirical success of robust RL algorithms and the non-asymptotic guarantees enjoyed by their non-robust counterparts. The key ideas in the paper also extend in a relatively straightforward fashion to robust Q-learning with function approximation.

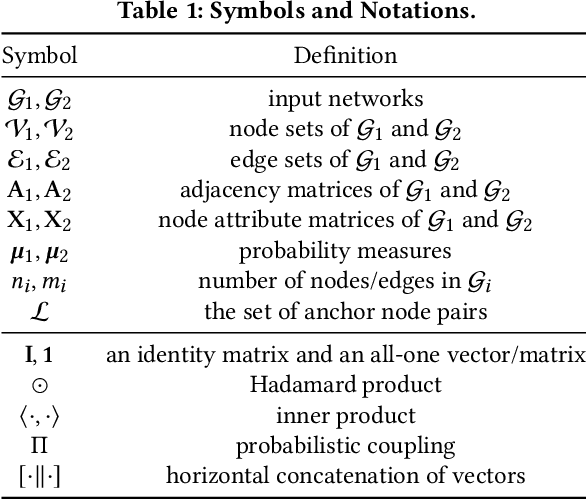
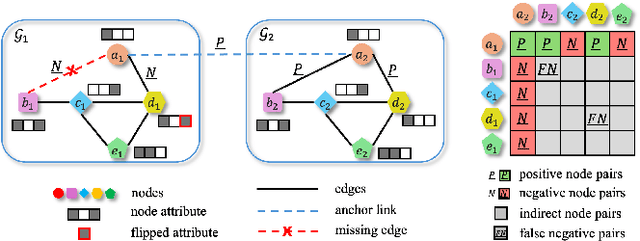
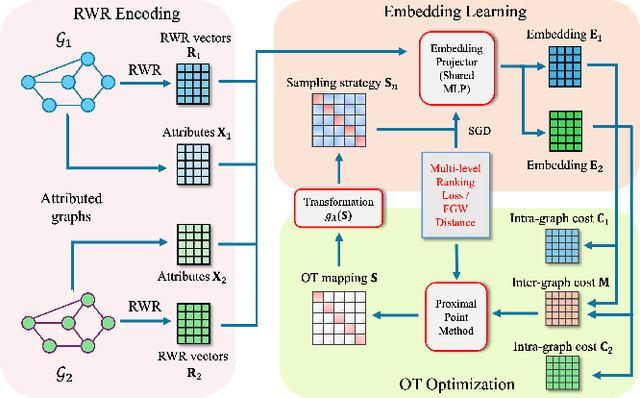
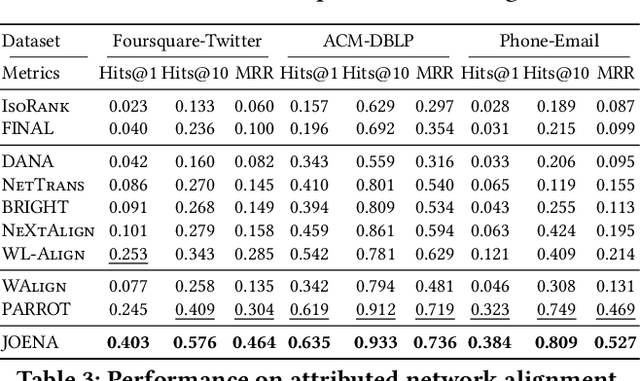
Joint Optimal Transport and Embedding for Network Alignment

Network alignment, which aims to find node correspondence across different networks, is the cornerstone of various downstream multi-network and Web mining tasks. Most of the embedding-based methods indirectly model cross-network node relationships by contrasting positive and negative node pairs sampled from hand-crafted strategies, which are vulnerable to graph noises and lead to potential misalignment of nodes. Another line of work based on the optimal transport (OT) theory directly models cross-network node relationships and generates noise-reduced alignments. However, OT methods heavily rely on fixed, pre-defined cost functions that prohibit end-to-end training and are hard to generalize. In this paper, we aim to unify the embedding and OT-based methods in a mutually beneficial manner and propose a joint optimal transport and embedding framework for network alignment named JOENA. For one thing (OT for embedding), through a simple yet effective transformation, the noise-reduced OT mapping serves as an adaptive sampling strategy directly modeling all cross-network node pairs for robust embedding learning.For another (embedding for OT), on top of the learned embeddings, the OT cost can be gradually trained in an end-to-end fashion, which further enhances the alignment quality. With a unified objective, the mutual benefits of both methods can be achieved by an alternating optimization schema with guaranteed convergence. Extensive experiments on real-world networks validate the effectiveness and scalability of JOENA, achieving up to 16% improvement in MRR and 20x speedup compared with the state-of-the-art alignment methods.

Reinforcement Learning with Segment Feedback

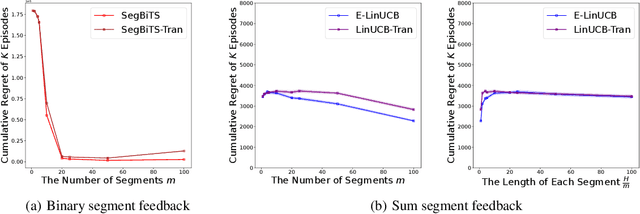
Standard reinforcement learning (RL) assumes that an agent can observe a reward for each state-action pair. However, in practical applications, it is often difficult and costly to collect a reward for each state-action pair. While there have been several works considering RL with trajectory feedback, it is unclear if trajectory feedback is inefficient for learning when trajectories are long. In this work, we consider a model named RL with segment feedback, which offers a general paradigm filling the gap between per-state-action feedback and trajectory feedback. In this model, we consider an episodic Markov decision process (MDP), where each episode is divided into $m$ segments, and the agent observes reward feedback only at the end of each segment. Under this model, we study two popular feedback settings: binary feedback and sum feedback, where the agent observes a binary outcome and a reward sum according to the underlying reward function, respectively. To investigate the impact of the number of segments $m$ on learning performance, we design efficient algorithms and establish regret upper and lower bounds for both feedback settings. Our theoretical and experimental results show that: under binary feedback, increasing the number of segments $m$ decreases the regret at an exponential rate; in contrast, surprisingly, under sum feedback, increasing $m$ does not reduce the regret significantly.

A Theoretical Analysis of Soft-Label vs Hard-Label Training in Neural Networks

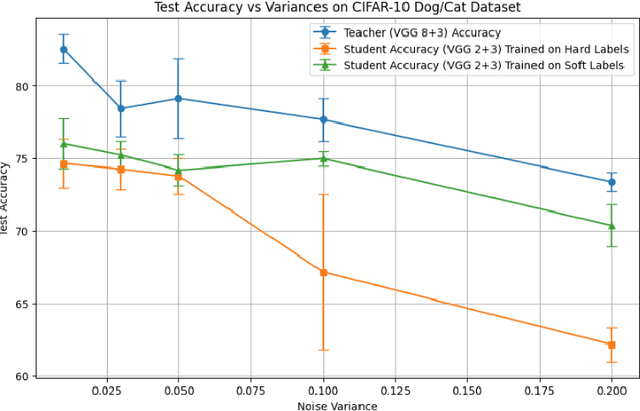
Knowledge distillation, where a small student model learns from a pre-trained large teacher model, has achieved substantial empirical success since the seminal work of \citep{hinton2015distilling}. Despite prior theoretical studies exploring the benefits of knowledge distillation, an important question remains unanswered: why does soft-label training from the teacher require significantly fewer neurons than directly training a small neural network with hard labels? To address this, we first present motivating experimental results using simple neural network models on a binary classification problem. These results demonstrate that soft-label training consistently outperforms hard-label training in accuracy, with the performance gap becoming more pronounced as the dataset becomes increasingly difficult to classify. We then substantiate these observations with a theoretical contribution based on two-layer neural network models. Specifically, we show that soft-label training using gradient descent requires only $O\left(\frac{1}{\gamma^2 \epsilon}\right)$ neurons to achieve a classification loss averaged over epochs smaller than some $\epsilon > 0$, where $\gamma$ is the separation margin of the limiting kernel. In contrast, hard-label training requires $O\left(\frac{1}{\gamma^4} \cdot \ln\left(\frac{1}{\epsilon}\right)\right)$ neurons, as derived from an adapted version of the gradient descent analysis in \citep{ji2020polylogarithmic}. This implies that when $\gamma \leq \epsilon$, i.e., when the dataset is challenging to classify, the neuron requirement for soft-label training can be significantly lower than that for hard-label training. Finally, we present experimental results on deep neural networks, further validating these theoretical findings.

Decentralized and Uncoordinated Learning of Stable Matchings: A Game-Theoretic Approach

We consider the problem of learning stable matchings in a fully decentralized and uncoordinated manner. In this problem, there are $n$ men and $n$ women, each having preference over the other side. It is assumed that women know their preferences over men, but men are not aware of their preferences over women, and they only learn them if they propose and successfully get matched to women. A matching is called stable if no man and woman prefer each other over their current matches. When all the preferences are known a priori, the celebrated Deferred-Acceptance algorithm proposed by Gale and Shapley provides a decentralized and uncoordinated algorithm to obtain a stable matching. However, when the preferences are unknown, developing such an algorithm faces major challenges due to a lack of coordination. We achieve this goal by making a connection between stable matchings and learning Nash equilibria (NE) in noncooperative games. First, we provide a complete information game formulation for the stable matching problem with known preferences such that its set of pure NE coincides with the set of stable matchings, while its mixed NE can be rounded in a decentralized manner to a stable matching. Relying on such a game-theoretic formulation, we show that for hierarchical markets, adopting the exponential weight (EXP) learning algorithm for the stable matching game achieves logarithmic regret with polynomial dependence on the number of players, thus answering a question posed in previous literature. Moreover, we show that the same EXP learning algorithm converges locally and exponentially fast to a stable matching in general matching markets. We complement this result by introducing another decentralized and uncoordinated learning algorithm that globally converges to a stable matching with arbitrarily high probability, leveraging the weak acyclicity property of the stable matching game.

Performance of NPG in Countable State-Space Average-Cost RL

We consider policy optimization methods in reinforcement learning settings where the state space is arbitrarily large, or even countably infinite. The motivation arises from control problems in communication networks, matching markets, and other queueing systems. We consider Natural Policy Gradient (NPG), which is a popular algorithm for finite state spaces. Under reasonable assumptions, we derive a performance bound for NPG that is independent of the size of the state space, provided the error in policy evaluation is within a factor of the true value function. We obtain this result by establishing new policy-independent bounds on the solution to Poisson's equation, i.e., the relative value function, and by combining these bounds with previously known connections between MDPs and learning from experts.

On the Global Convergence of Policy Gradient in Average Reward Markov Decision Processes

We present the first finite time global convergence analysis of policy gradient in the context of infinite horizon average reward Markov decision processes (MDPs). Specifically, we focus on ergodic tabular MDPs with finite state and action spaces. Our analysis shows that the policy gradient iterates converge to the optimal policy at a sublinear rate of $O\left({\frac{1}{T}}\right),$ which translates to $O\left({\log(T)}\right)$ regret, where $T$ represents the number of iterations. Prior work on performance bounds for discounted reward MDPs cannot be extended to average reward MDPs because the bounds grow proportional to the fifth power of the effective horizon. Thus, our primary contribution is in proving that the policy gradient algorithm converges for average-reward MDPs and in obtaining finite-time performance guarantees. In contrast to the existing discounted reward performance bounds, our performance bounds have an explicit dependence on constants that capture the complexity of the underlying MDP. Motivated by this observation, we reexamine and improve the existing performance bounds for discounted reward MDPs. We also present simulations to empirically evaluate the performance of average reward policy gradient algorithm.

Exploration-Driven Policy Optimization in RLHF: Theoretical Insights on Efficient Data Utilization

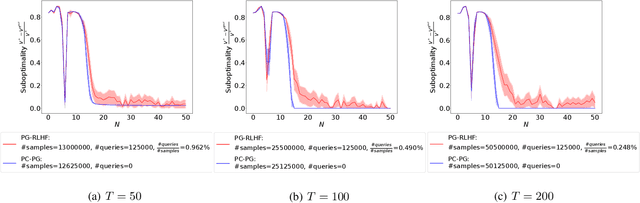
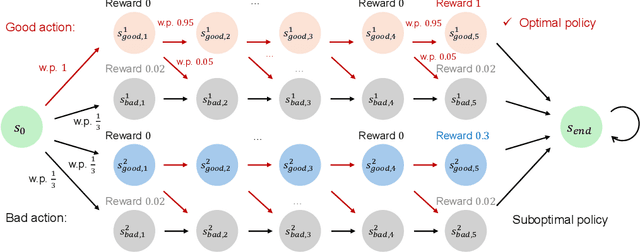
Reinforcement Learning from Human Feedback (RLHF) has achieved impressive empirical successes while relying on a small amount of human feedback. However, there is limited theoretical justification for this phenomenon. Additionally, most recent studies focus on value-based algorithms despite the recent empirical successes of policy-based algorithms. In this work, we consider an RLHF algorithm based on policy optimization (PO-RLHF). The algorithm is based on the popular Policy Cover-Policy Gradient (PC-PG) algorithm, which assumes knowledge of the reward function. In PO-RLHF, knowledge of the reward function is not assumed and the algorithm relies on trajectory-based comparison feedback to infer the reward function. We provide performance bounds for PO-RLHF with low query complexity, which provides insight into why a small amount of human feedback may be sufficient to get good performance with RLHF. A key novelty is our trajectory-level elliptical potential analysis technique used to infer reward function parameters when comparison queries rather than reward observations are used. We provide and analyze algorithms in two settings: linear and neural function approximation, PG-RLHF and NN-PG-RLHF, respectively.

Convergence for Natural Policy Gradient on Infinite-State Average-Reward Markov Decision Processes

Infinite-state Markov Decision Processes (MDPs) are essential in modeling and optimizing a wide variety of engineering problems. In the reinforcement learning (RL) context, a variety of algorithms have been developed to learn and optimize these MDPs. At the heart of many popular policy-gradient based learning algorithms, such as natural actor-critic, TRPO, and PPO, lies the Natural Policy Gradient (NPG) algorithm. Convergence results for these RL algorithms rest on convergence results for the NPG algorithm. However, all existing results on the convergence of the NPG algorithm are limited to finite-state settings. We prove the first convergence rate bound for the NPG algorithm for infinite-state average-reward MDPs, proving a $O(1/\sqrt{T})$ convergence rate, if the NPG algorithm is initialized with a good initial policy. Moreover, we show that in the context of a large class of queueing MDPs, the MaxWeight policy suffices to satisfy our initial-policy requirement and achieve a $O(1/\sqrt{T})$ convergence rate. Key to our result are state-dependent bounds on the relative value function achieved by the iterate policies of the NPG algorithm.

Rates of Convergence in the Central Limit Theorem for Markov Chains, with an Application to TD Learning

We prove a non-asymptotic central limit theorem for vector-valued martingale differences using Stein's method, and use Poisson's equation to extend the result to functions of Markov Chains. We then show that these results can be applied to establish a non-asymptotic central limit theorem for Temporal Difference (TD) learning with averaging.