Anna Winnicki
Reinforcement Learning with Segment Feedback
Feb 03, 2025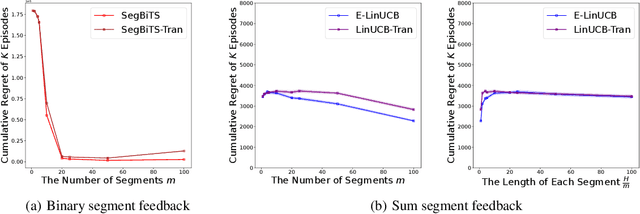
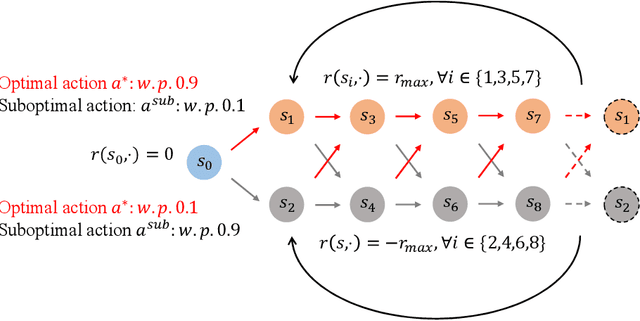
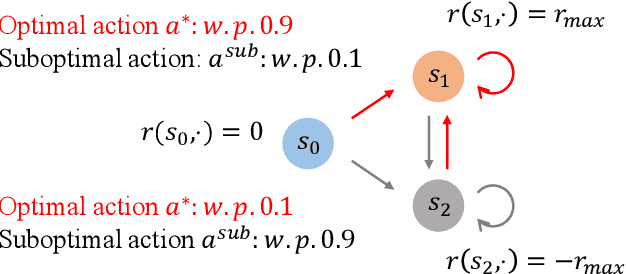
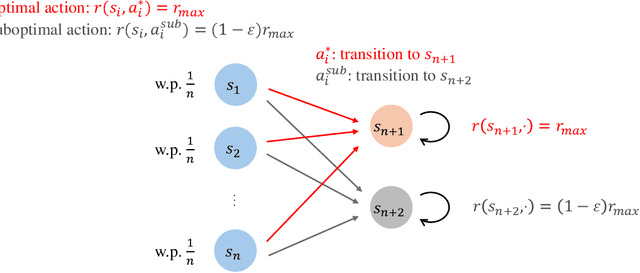
Abstract:Standard reinforcement learning (RL) assumes that an agent can observe a reward for each state-action pair. However, in practical applications, it is often difficult and costly to collect a reward for each state-action pair. While there have been several works considering RL with trajectory feedback, it is unclear if trajectory feedback is inefficient for learning when trajectories are long. In this work, we consider a model named RL with segment feedback, which offers a general paradigm filling the gap between per-state-action feedback and trajectory feedback. In this model, we consider an episodic Markov decision process (MDP), where each episode is divided into $m$ segments, and the agent observes reward feedback only at the end of each segment. Under this model, we study two popular feedback settings: binary feedback and sum feedback, where the agent observes a binary outcome and a reward sum according to the underlying reward function, respectively. To investigate the impact of the number of segments $m$ on learning performance, we design efficient algorithms and establish regret upper and lower bounds for both feedback settings. Our theoretical and experimental results show that: under binary feedback, increasing the number of segments $m$ decreases the regret at an exponential rate; in contrast, surprisingly, under sum feedback, increasing $m$ does not reduce the regret significantly.
Exploration-Driven Policy Optimization in RLHF: Theoretical Insights on Efficient Data Utilization
Feb 15, 2024
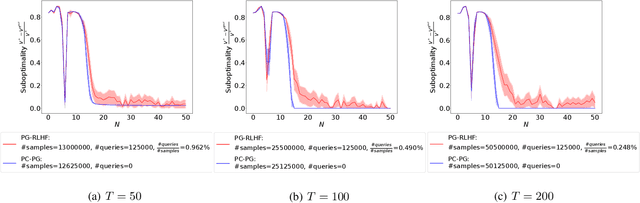
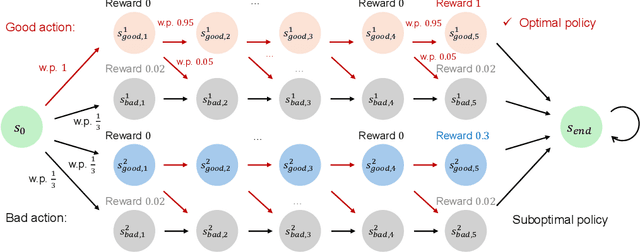
Abstract:Reinforcement Learning from Human Feedback (RLHF) has achieved impressive empirical successes while relying on a small amount of human feedback. However, there is limited theoretical justification for this phenomenon. Additionally, most recent studies focus on value-based algorithms despite the recent empirical successes of policy-based algorithms. In this work, we consider an RLHF algorithm based on policy optimization (PO-RLHF). The algorithm is based on the popular Policy Cover-Policy Gradient (PC-PG) algorithm, which assumes knowledge of the reward function. In PO-RLHF, knowledge of the reward function is not assumed and the algorithm relies on trajectory-based comparison feedback to infer the reward function. We provide performance bounds for PO-RLHF with low query complexity, which provides insight into why a small amount of human feedback may be sufficient to get good performance with RLHF. A key novelty is our trajectory-level elliptical potential analysis technique used to infer reward function parameters when comparison queries rather than reward observations are used. We provide and analyze algorithms in two settings: linear and neural function approximation, PG-RLHF and NN-PG-RLHF, respectively.
A New Policy Iteration Algorithm For Reinforcement Learning in Zero-Sum Markov Games
Mar 17, 2023Abstract:Many model-based reinforcement learning (RL) algorithms can be viewed as having two phases that are iteratively implemented: a learning phase where the model is approximately learned and a planning phase where the learned model is used to derive a policy. In the case of standard MDPs, the learning problem can be solved using either value iteration or policy iteration. However, in the case of zero-sum Markov games, there is no efficient policy iteration algorithm; e.g., it has been shown in Hansen et al. (2013) that one has to solve Omega(1/(1-alpha)) MDPs, where alpha is the discount factor, to implement the only known convergent version of policy iteration. Another algorithm for Markov zero-sum games, called naive policy iteration, is easy to implement but is only provably convergent under very restrictive assumptions. Prior attempts to fix naive policy iteration algorithm have several limitations. Here, we show that a simple variant of naive policy iteration for games converges, and converges exponentially fast. The only addition we propose to naive policy iteration is the use of lookahead in the policy improvement phase. This is appealing because lookahead is anyway often used in RL for games. We further show that lookahead can be implemented efficiently in linear Markov games, which are the counterpart of the linear MDPs and have been the subject of much attention recently. We then consider multi-agent reinforcement learning which uses our algorithm in the planning phases, and provide sample and time complexity bounds for such an algorithm.
On The Convergence Of Policy Iteration-Based Reinforcement Learning With Monte Carlo Policy Evaluation
Jan 23, 2023Abstract:A common technique in reinforcement learning is to evaluate the value function from Monte Carlo simulations of a given policy, and use the estimated value function to obtain a new policy which is greedy with respect to the estimated value function. A well-known longstanding open problem in this context is to prove the convergence of such a scheme when the value function of a policy is estimated from data collected from a single sample path obtained from implementing the policy (see page 99 of [Sutton and Barto, 2018], page 8 of [Tsitsiklis, 2002]). We present a solution to the open problem by showing that a first-visit version of such a policy iteration scheme indeed converges to the optimal policy provided that the policy improvement step uses lookahead [Silver et al., 2016, Mnih et al., 2016, Silver et al., 2017b] rather than a simple greedy policy improvement. We provide results both for the original open problem in the tabular setting and also present extensions to the function approximation setting, where we show that the policy resulting from the algorithm performs close to the optimal policy within a function approximation error.
Reinforcement Learning with Unbiased Policy Evaluation and Linear Function Approximation
Oct 13, 2022Abstract:We provide performance guarantees for a variant of simulation-based policy iteration for controlling Markov decision processes that involves the use of stochastic approximation algorithms along with state-of-the-art techniques that are useful for very large MDPs, including lookahead, function approximation, and gradient descent. Specifically, we analyze two algorithms; the first algorithm involves a least squares approach where a new set of weights associated with feature vectors is obtained via least squares minimization at each iteration and the second algorithm involves a two-time-scale stochastic approximation algorithm taking several steps of gradient descent towards the least squares solution before obtaining the next iterate using a stochastic approximation algorithm.
The Role of Lookahead and Approximate Policy Evaluation in Policy Iteration with Linear Value Function Approximation
Sep 28, 2021
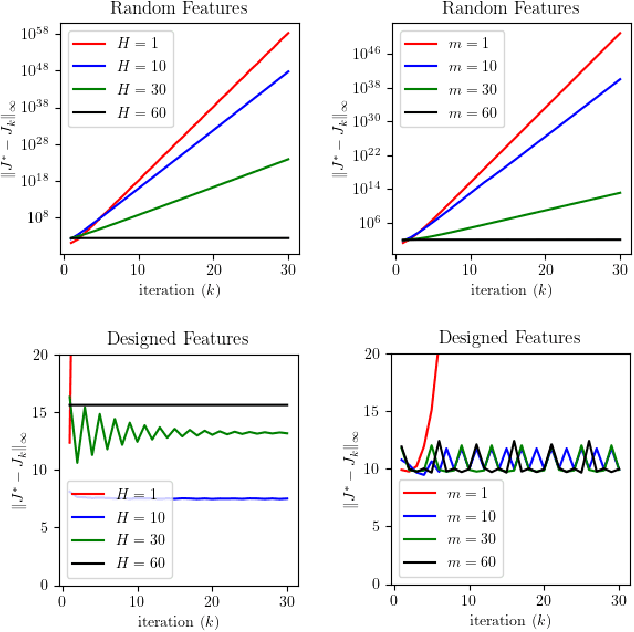
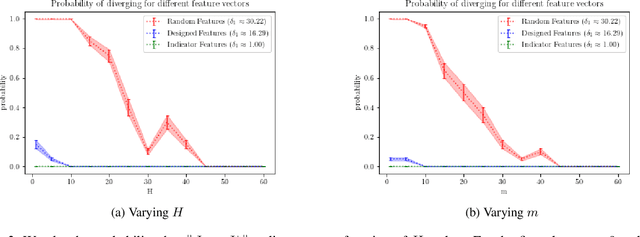
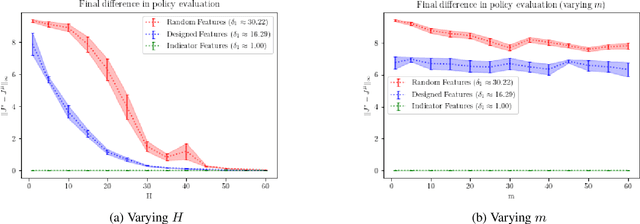
Abstract:When the sizes of the state and action spaces are large, solving MDPs can be computationally prohibitive even if the probability transition matrix is known. So in practice, a number of techniques are used to approximately solve the dynamic programming problem, including lookahead, approximate policy evaluation using an m-step return, and function approximation. In a recent paper, (Efroni et al. 2019) studied the impact of lookahead on the convergence rate of approximate dynamic programming. In this paper, we show that these convergence results change dramatically when function approximation is used in conjunction with lookout and approximate policy evaluation using an m-step return. Specifically, we show that when linear function approximation is used to represent the value function, a certain minimum amount of lookahead and multi-step return is needed for the algorithm to even converge. And when this condition is met, we characterize the finite-time performance of policies obtained using such approximate policy iteration. Our results are presented for two different procedures to compute the function approximation: linear least-squares regression and gradient descent.
Optimistic Policy Iteration for MDPs with Acyclic Transient State Structure
Feb 13, 2021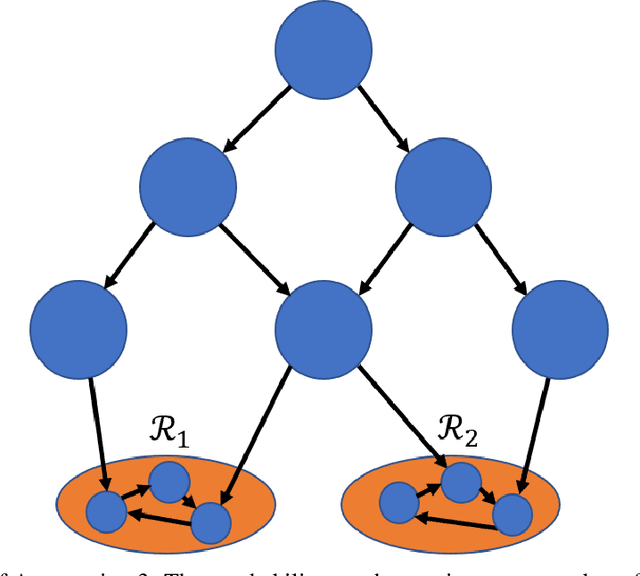
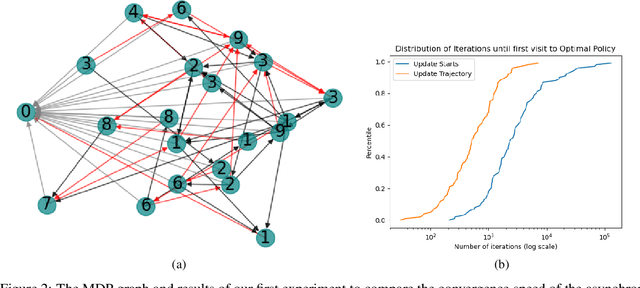
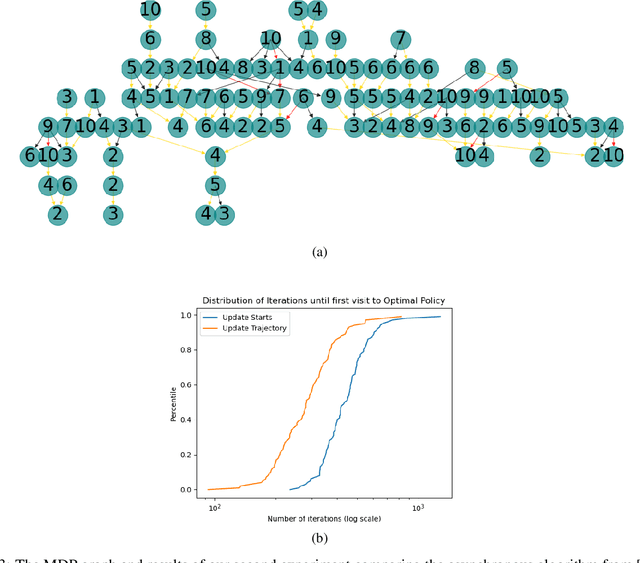
Abstract:We consider Markov Decision Processes (MDPs) in which every stationary policy induces the same graph structure for the underlying Markov chain and further, the graph has the following property: if we replace each recurrent class by a node, then the resulting graph is acyclic. For such MDPs, we prove the convergence of the stochastic dynamics associated with a version of optimistic policy iteration (OPI), suggested in Tsitsiklis (2002), in which the values associated with all the nodes visited during each iteration of the OPI are updated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge