Optimistic Policy Iteration for MDPs with Acyclic Transient State Structure
Paper and Code
Feb 13, 2021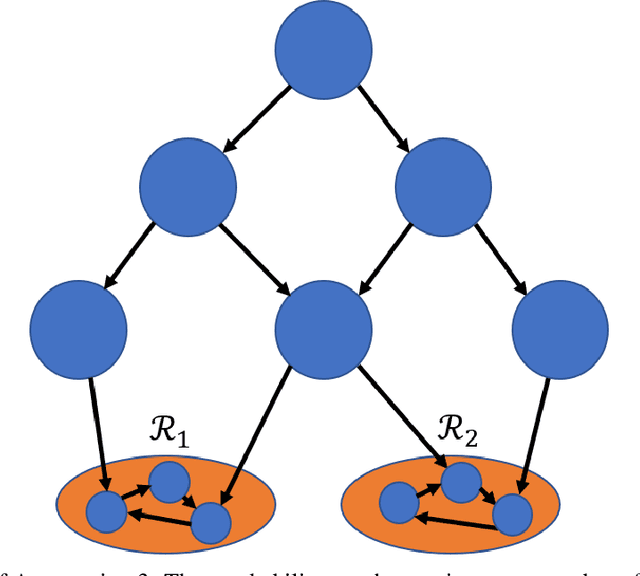
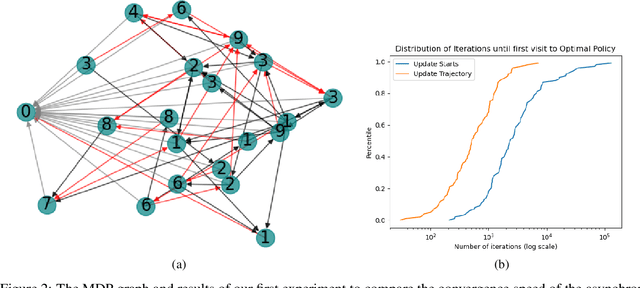
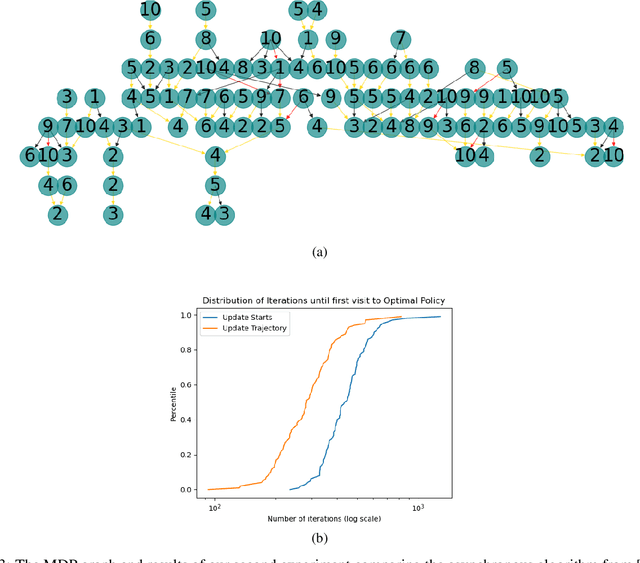
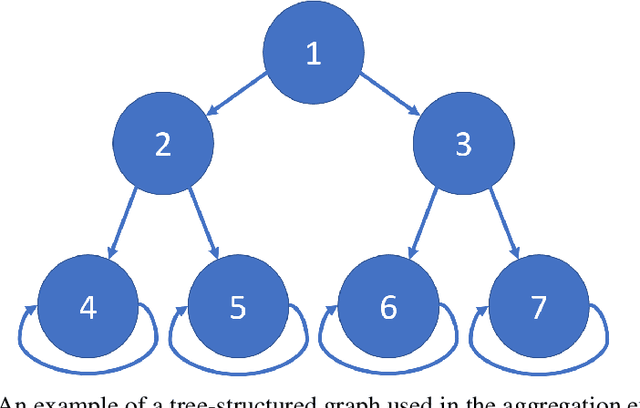
We consider Markov Decision Processes (MDPs) in which every stationary policy induces the same graph structure for the underlying Markov chain and further, the graph has the following property: if we replace each recurrent class by a node, then the resulting graph is acyclic. For such MDPs, we prove the convergence of the stochastic dynamics associated with a version of optimistic policy iteration (OPI), suggested in Tsitsiklis (2002), in which the values associated with all the nodes visited during each iteration of the OPI are updated.
* 16 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge