The Role of Lookahead and Approximate Policy Evaluation in Policy Iteration with Linear Value Function Approximation

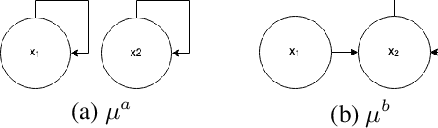
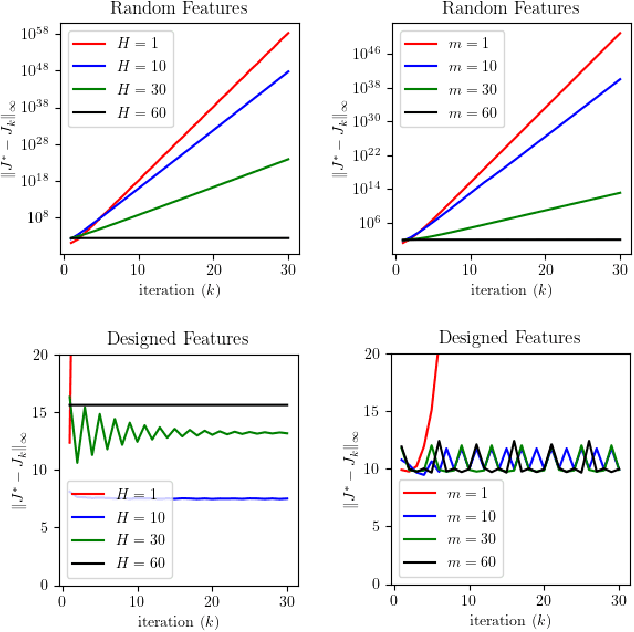
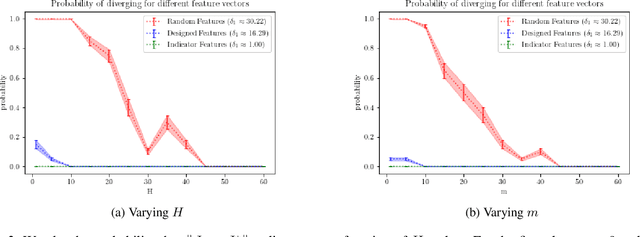
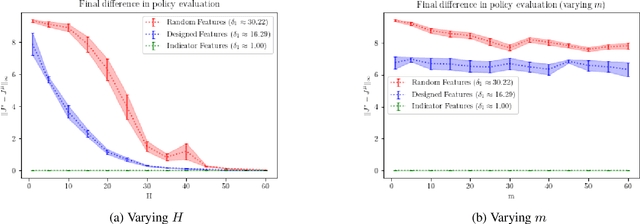
When the sizes of the state and action spaces are large, solving MDPs can be computationally prohibitive even if the probability transition matrix is known. So in practice, a number of techniques are used to approximately solve the dynamic programming problem, including lookahead, approximate policy evaluation using an m-step return, and function approximation. In a recent paper, (Efroni et al. 2019) studied the impact of lookahead on the convergence rate of approximate dynamic programming. In this paper, we show that these convergence results change dramatically when function approximation is used in conjunction with lookout and approximate policy evaluation using an m-step return. Specifically, we show that when linear function approximation is used to represent the value function, a certain minimum amount of lookahead and multi-step return is needed for the algorithm to even converge. And when this condition is met, we characterize the finite-time performance of policies obtained using such approximate policy iteration. Our results are presented for two different procedures to compute the function approximation: linear least-squares regression and gradient descent.

Optimistic Policy Iteration for MDPs with Acyclic Transient State Structure

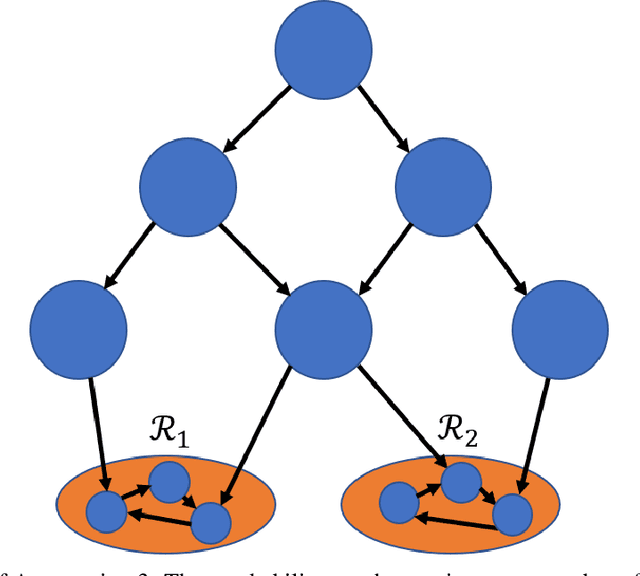
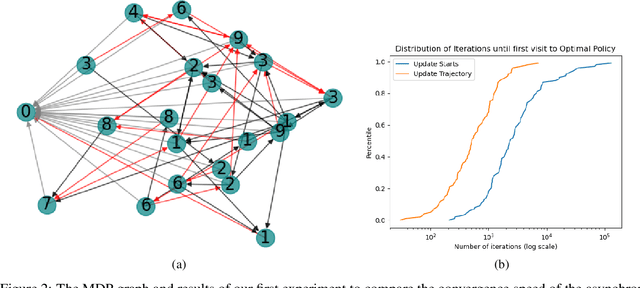
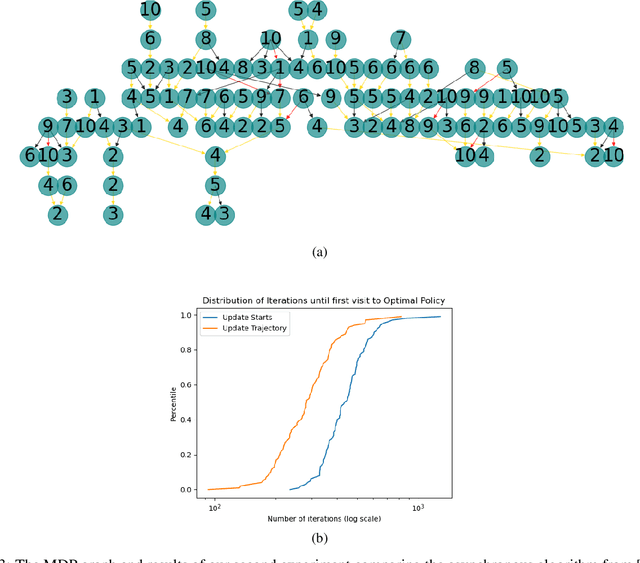
We consider Markov Decision Processes (MDPs) in which every stationary policy induces the same graph structure for the underlying Markov chain and further, the graph has the following property: if we replace each recurrent class by a node, then the resulting graph is acyclic. For such MDPs, we prove the convergence of the stochastic dynamics associated with a version of optimistic policy iteration (OPI), suggested in Tsitsiklis (2002), in which the values associated with all the nodes visited during each iteration of the OPI are updated.

Combining Reinforcement Learning with Model Predictive Control for On-Ramp Merging

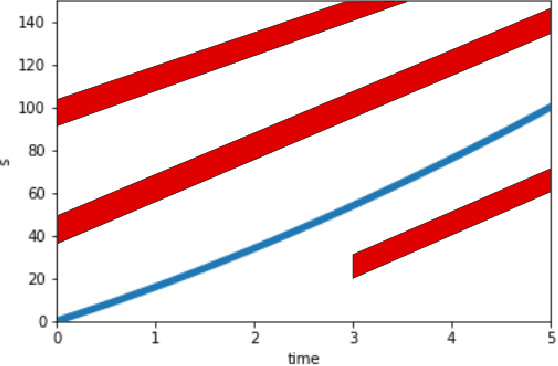
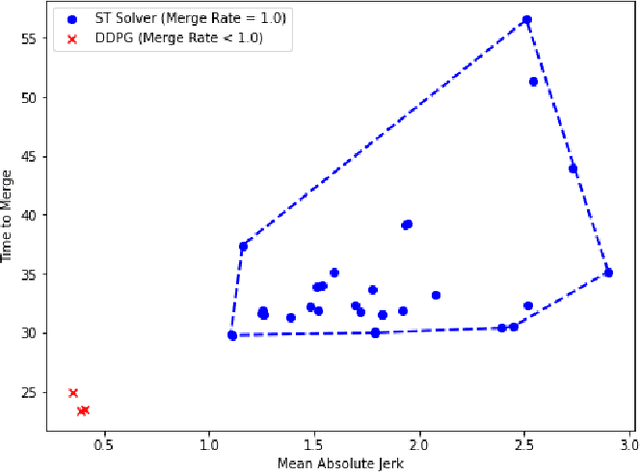
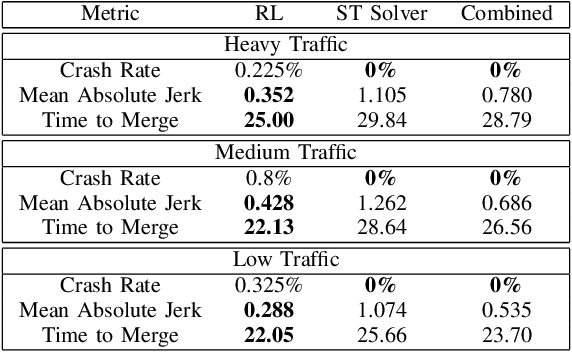
We consider the problem of designing an algorithm to allow a car to autonomously merge on to a highway from an on-ramp. Two broad classes of techniques have been proposed to solve motion planning problems in autonomous driving: Model Predictive Control (MPC) and Reinforcement Learning (RL). In this paper, we first establish the strengths and weaknesses of state-of-the-art MPC and RL-based techniques through simulations. We show that the performance of the RL agent is worse than that of the MPC solution from the perspective of safety and robustness to out-of-distribution traffic patterns, i.e., traffic patterns which were not seen by the RL agent during training. On the other hand, the performance of the RL agent is better than that of the MPC solution when it comes to efficiency and passenger comfort. We subsequently present an algorithm which blends the model-free RL agent with the MPC solution and show that it provides better trade-offs between all metrics -- passenger comfort, efficiency, crash rate and robustness.