Decentralized and Uncoordinated Learning of Stable Matchings: A Game-Theoretic Approach

We consider the problem of learning stable matchings in a fully decentralized and uncoordinated manner. In this problem, there are $n$ men and $n$ women, each having preference over the other side. It is assumed that women know their preferences over men, but men are not aware of their preferences over women, and they only learn them if they propose and successfully get matched to women. A matching is called stable if no man and woman prefer each other over their current matches. When all the preferences are known a priori, the celebrated Deferred-Acceptance algorithm proposed by Gale and Shapley provides a decentralized and uncoordinated algorithm to obtain a stable matching. However, when the preferences are unknown, developing such an algorithm faces major challenges due to a lack of coordination. We achieve this goal by making a connection between stable matchings and learning Nash equilibria (NE) in noncooperative games. First, we provide a complete information game formulation for the stable matching problem with known preferences such that its set of pure NE coincides with the set of stable matchings, while its mixed NE can be rounded in a decentralized manner to a stable matching. Relying on such a game-theoretic formulation, we show that for hierarchical markets, adopting the exponential weight (EXP) learning algorithm for the stable matching game achieves logarithmic regret with polynomial dependence on the number of players, thus answering a question posed in previous literature. Moreover, we show that the same EXP learning algorithm converges locally and exponentially fast to a stable matching in general matching markets. We complement this result by introducing another decentralized and uncoordinated learning algorithm that globally converges to a stable matching with arbitrarily high probability, leveraging the weak acyclicity property of the stable matching game.

Optimizing Profitability in Timely Gossip Networks

We consider a communication system where a group of users, interconnected in a bidirectional gossip network, wishes to follow a time-varying source, e.g., updates on an event, in real-time. The users wish to maintain their expected version ages below a threshold, and can either rely on gossip from their neighbors or directly subscribe to a server publishing about the event, if the former option does not meet the timeliness requirements. The server wishes to maximize its profit by increasing subscriptions from users and minimizing event sampling frequency to reduce costs. This leads to a Stackelberg game between the server and the users where the sender is the leader deciding its sampling frequency and the users are the followers deciding their subscription strategies. We investigate equilibrium strategies for low-connectivity and high-connectivity topologies.

How to Make Money From Fresh Data: Subscription Strategies in Age-Based Systems

We consider a communication system consisting of a server that tracks and publishes updates about a time-varying data source or event, and a gossip network of users interested in closely tracking the event. The timeliness of the information is measured through the version age of information. The users wish to have their expected version ages remain below a threshold, and have the option to either rely on gossip from their neighbors or subscribe to the server directly to follow updates about the event if the former option does not meet the timeliness requirements. The server wishes to maximize its profit by increasing the number of subscribers and reducing costs associated with the frequent sampling of the event. We model the problem setup as a Stackelberg game between the server and the users, where the server commits to a frequency of sampling the event, and the users make decisions on whether to subscribe or not. As an initial work, we focus on directed networks with unidirectional flow of information and obtain the optimal equilibrium strategies for all the players. We provide simulation results to confirm the theoretical findings and provide additional insights.

Learning How to Strategically Disclose Information

Strategic information disclosure, in its simplest form, considers a game between an information provider (sender) who has access to some private information that an information receiver is interested in. While the receiver takes an action that affects the utilities of both players, the sender can design information (or modify beliefs) of the receiver through signal commitment, hence posing a Stackelberg game. However, obtaining a Stackelberg equilibrium for this game traditionally requires the sender to have access to the receiver's objective. In this work, we consider an online version of information design where a sender interacts with a receiver of an unknown type who is adversarially chosen at each round. Restricting attention to Gaussian prior and quadratic costs for the sender and the receiver, we show that $\mathcal{O}(\sqrt{T})$ regret is achievable with full information feedback, where $T$ is the total number of interactions between the sender and the receiver. Further, we propose a novel parametrization that allows the sender to achieve $\mathcal{O}(\sqrt{T})$ regret for a general convex utility function. We then consider the Bayesian Persuasion problem with an additional cost term in the objective function, which penalizes signaling policies that are more informative and obtain $\mathcal{O}(\log(T))$ regret. Finally, we establish a sublinear regret bound for the partial information feedback setting and provide simulations to support our theoretical results.

Scalable and Independent Learning of Nash Equilibrium Policies in $n$-Player Stochastic Games with Unknown Independent Chains

We study a subclass of $n$-player stochastic games, namely, stochastic games with independent chains and unknown transition matrices. In this class of games, players control their own internal Markov chains whose transitions do not depend on the states/actions of other players. However, players' decisions are coupled through their payoff functions. We assume players can receive only realizations of their payoffs, and that the players can not observe the states and actions of other players, nor do they know the transition probability matrices of their own Markov chain. Relying on a compact dual formulation of the game based on occupancy measures and the technique of confidence set to maintain high-probability estimates of the unknown transition matrices, we propose a fully decentralized mirror descent algorithm to learn an $\epsilon$-NE for this class of games. The proposed algorithm has the desired properties of independence, scalability, and convergence. Specifically, under no assumptions on the reward functions, we show the proposed algorithm converges in polynomial time in a weaker distance (namely, the averaged Nikaido-Isoda gap) to the set of $\epsilon$-NE policies with arbitrarily high probability. Moreover, assuming the existence of a variationally stable Nash equilibrium policy, we show that the proposed algorithm converges asymptotically to the stable $\epsilon$-NE policy with arbitrarily high probability. In addition to Markov potential games and linear-quadratic stochastic games, this work provides another subclass of $n$-player stochastic games that, under some mild assumptions, admit polynomial-time learning algorithms for finding their stationary $\epsilon$-NE policies.

Online Reinforcement Learning in Markov Decision Process Using Linear Programming

We consider online reinforcement learning in episodic Markov decision process (MDP) with an unknown transition matrix and stochastic rewards drawn from a fixed but unknown distribution. The learner aims to learn the optimal policy and minimize their regret over a finite time horizon through interacting with the environment. We devise a simple and efficient model-based algorithm that achieves $\tilde{O}(LX\sqrt{TA})$ regret with high probability, where $L$ is the episode length, $T$ is the number of episodes, and $X$ and $A$ are the cardinalities of the state space and the action space, respectively. The proposed algorithm, which is based on the concept of "optimism in the face of uncertainty", maintains confidence sets of transition and reward functions and uses occupancy measures to connect the online MDP with linear programming. It achieves a tighter regret bound compared to the existing works that use a similar confidence sets framework and improves the computational effort compared to those that use a different framework but with a slightly tighter regret bound.

The Role of Local Steps in Local SGD

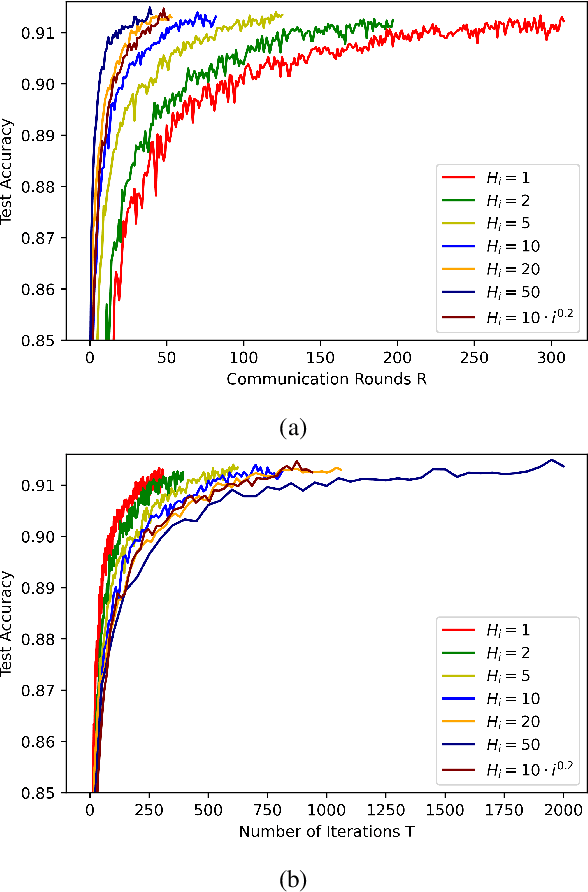
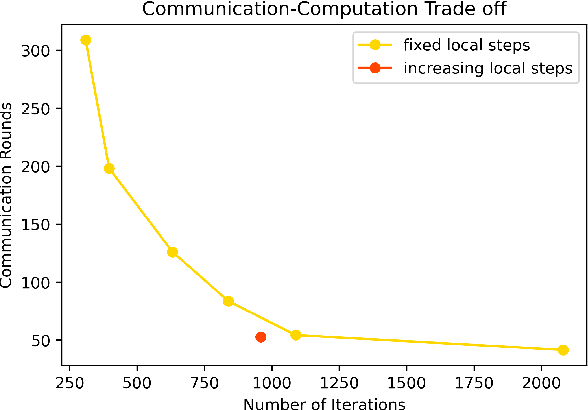
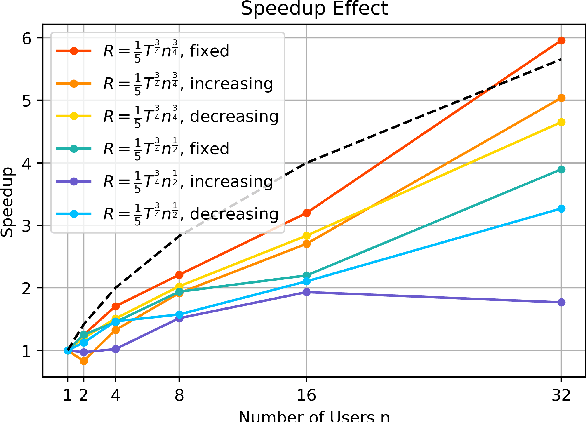
We consider the distributed stochastic optimization problem where $n$ agents want to minimize a global function given by the sum of agents' local functions, and focus on the heterogeneous setting when agents' local functions are defined over non-i.i.d. data sets. We study the Local SGD method, where agents perform a number of local stochastic gradient steps and occasionally communicate with a central node to improve their local optimization tasks. We analyze the effect of local steps on the convergence rate and the communication complexity of Local SGD. In particular, instead of assuming a fixed number of local steps across all communication rounds, we allow the number of local steps during the $i$-th communication round, $H_i$, to be different and arbitrary numbers. Our main contribution is to characterize the convergence rate of Local SGD as a function of $\{H_i\}_{i=1}^R$ under various settings of strongly convex, convex, and nonconvex local functions, where $R$ is the total number of communication rounds. Based on this characterization, we provide sufficient conditions on the sequence $\{H_i\}_{i=1}^R$ such that Local SGD can achieve linear speed-up with respect to the number of workers. Furthermore, we propose a new communication strategy with increasing local steps superior to existing communication strategies for strongly convex local functions. On the other hand, for convex and nonconvex local functions, we argue that fixed local steps are the best communication strategy for Local SGD and recover state-of-the-art convergence rate results. Finally, we justify our theoretical results through extensive numerical experiments.

Faster Convergence of Local SGD for Over-Parameterized Models

Modern machine learning architectures are often highly expressive. They are usually over-parameterized and can interpolate the data by driving the empirical loss close to zero. We analyze the convergence of Local SGD (or FedAvg) for such over-parameterized models in the heterogeneous data setting and improve upon the existing literature by establishing the following convergence rates. We show an error bound of $\O(\exp(-T))$ for strongly-convex loss functions, where $T$ is the total number of iterations. For general convex loss functions, we establish an error bound of $\O(1/T)$ under a mild data similarity assumption and an error bound of $\O(K/T)$ otherwise, where $K$ is the number of local steps. We also extend our results for non-convex loss functions by proving an error bound of $\O(K/T)$. Before our work, the best-known convergence rate for strongly-convex loss functions was $\O(\exp(-T/K))$, and none existed for general convex or non-convex loss functions under the overparameterized setting. We complete our results by providing problem instances in which such convergence rates are tight to a constant factor under a reasonably small stepsize scheme. Finally, we validate our theoretical results using numerical experiments on real and synthetic data.

Learning Stationary Nash Equilibrium Policies in $n$-Player Stochastic Games with Independent Chains via Dual Mirror Descent

We consider a subclass of $n$-player stochastic games, in which players have their own internal state/action spaces while they are coupled through their payoff functions. It is assumed that players' internal chains are driven by independent transition probabilities. Moreover, players can only receive realizations of their payoffs but not the actual functions, nor can they observe each others' states/actions. Under some assumptions on the structure of the payoff functions, we develop efficient learning algorithms based on Dual Averaging and Dual Mirror Descent, which provably converge almost surely or in expectation to the set of $\epsilon$-Nash equilibrium policies. In particular, we derive upper bounds on the number of iterates that scale polynomially in terms of the game parameters to achieve an $\epsilon$-Nash equilibrium policy. Besides Markov potential games and linear-quadratic stochastic games, this work provides another interesting subclass of $n$-player stochastic games that under some assumption provably admit polynomial-time learning algorithm for finding their $\epsilon$-Nash equilibrium policies.

The Role of Gossiping for Information Dissemination over Networked Agents

We consider information dissemination over a network of gossiping agents (nodes). In this model, a source keeps the most up-to-date information about a time-varying binary state of the world, and $n$ receiver nodes want to follow the information at the source as accurately as possible. When the information at the source changes, the source first sends updates to a subset of $m\leq n$ nodes. After that, the nodes share their local information during the gossiping period to disseminate the information further. The nodes then estimate the information at the source using the majority rule at the end of the gossiping period. To analyze information dissemination, we introduce a new error metric to find the average percentage of nodes that can accurately obtain the most up-to-date information at the source. We characterize the equations necessary to obtain the steady-state distribution for the average error and then analyze the system behavior under both high and low gossip rates. In the high gossip rate, in which each node can access other nodes' information more frequently, we show that the nodes update their information based on the majority of the information in the network. In the low gossip rate, we introduce and analyze the gossip gain, which is the reduction at the average error due to gossiping. In particular, we develop an adaptive policy that the source can use to determine its current transmission capacity $m$ based on its past transmission rates and the accuracy of the information at the nodes. In numerical results, we show that when the source's transmission capacity $m$ is limited, gossiping can be harmful as it causes incorrect information to disseminate. We then find the optimal gossip rates to minimize the average error for a fixed $m$. Finally, we illustrate the outperformance of our adaptive policy compared to the constant $m$-selection policy even for the high gossip rates.