Online Learning for Dynamic Vickrey-Clarke-Groves Mechanism in Sequential Auctions under Unknown Environments

We consider the problem of online dynamic mechanism design for sequential auctions in unknown environments, where the underlying market and, thus, the bidders' values vary over time as interactions between the seller and the bidders progress. We model the sequential auctions as an infinite-horizon average-reward Markov decision process (MDP), where the transition kernel and reward functions are unknown to the seller. In each round, the seller determines an allocation and a payment for each bidder. Each bidder receives a private reward and submits a sealed bid to the seller. The state, which represents the underlying market, evolves according to an unknown transition kernel and the seller's allocation policy. Unlike existing works that formulate the problem as a multi-armed bandit model or as an episodic MDP, where the environment resets to an initial state after each round or episode, our paper considers a more realistic and sophisticated setting in which the market continues to evolve without restarting. We first extend the Vickrey-Clarke-Groves (VCG) mechanism, which is known to be efficient, truthful, and individually rational for one-shot static auctions, to sequential auctions, thereby obtaining a dynamic VCG mechanism counterpart that preserves these desired properties. We then focus on the online setting and develop an online reinforcement learning algorithm for the seller to learn the underlying MDP model and implement a mechanism that closely resembles the dynamic VCG mechanism. We show that the learned online mechanism asymptotically converges to a dynamic mechanism that approximately satisfies efficiency, truthfulness, and individual rationality with arbitrarily high probability and achieves guaranteed performance in terms of various notions of regret.

Online Reinforcement Learning in Markov Decision Process Using Linear Programming

We consider online reinforcement learning in episodic Markov decision process (MDP) with an unknown transition matrix and stochastic rewards drawn from a fixed but unknown distribution. The learner aims to learn the optimal policy and minimize their regret over a finite time horizon through interacting with the environment. We devise a simple and efficient model-based algorithm that achieves $\tilde{O}(LX\sqrt{TA})$ regret with high probability, where $L$ is the episode length, $T$ is the number of episodes, and $X$ and $A$ are the cardinalities of the state space and the action space, respectively. The proposed algorithm, which is based on the concept of "optimism in the face of uncertainty", maintains confidence sets of transition and reward functions and uses occupancy measures to connect the online MDP with linear programming. It achieves a tighter regret bound compared to the existing works that use a similar confidence sets framework and improves the computational effort compared to those that use a different framework but with a slightly tighter regret bound.

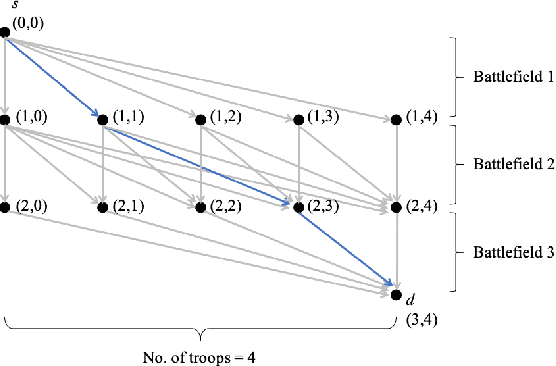
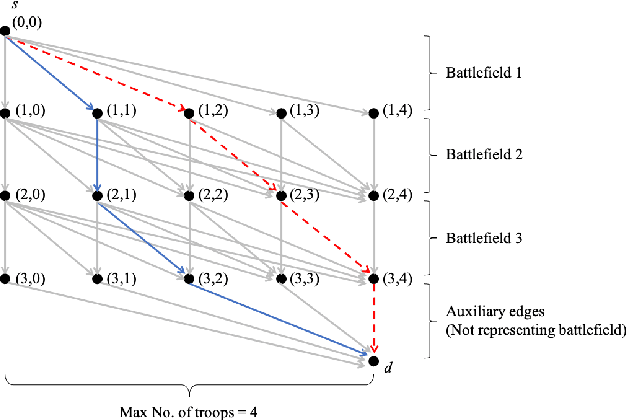
Bandit Learning for Dynamic Colonel Blotto Game with a Budget Constraint

We consider a dynamic Colonel Blotto game (CBG) in which one of the players is the learner and has limited troops (budget) to allocate over a finite time horizon. At each stage, the learner strategically determines the budget and its distribution to allocate among the battlefields based on past observations. The other player is the adversary, who chooses its budget allocation strategies randomly from some fixed but unknown distribution. The learner's objective is to minimize the regret, which is defined as the difference between the optimal payoff in terms of the best dynamic policy and the realized payoff by following a learning algorithm. The dynamic CBG is analyzed under the framework of combinatorial bandit and bandit with knapsacks. We first convert the dynamic CBG with the budget constraint to a path planning problem on a graph. We then devise an efficient dynamic policy for the learner that uses a combinatorial bandit algorithm Edge on the path planning graph as a subroutine for another algorithm LagrangeBwK. A high-probability regret bound is derived, and it is shown that under the proposed policy, the learner's regret in the budget-constrained dynamic CBG matches (up to a logarithmic factor) that of the repeated CBG without budget constraints.