ADMM for Downlink Beamforming in Cell-Free Massive MIMO Systems

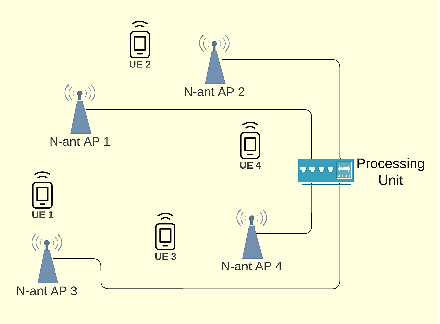
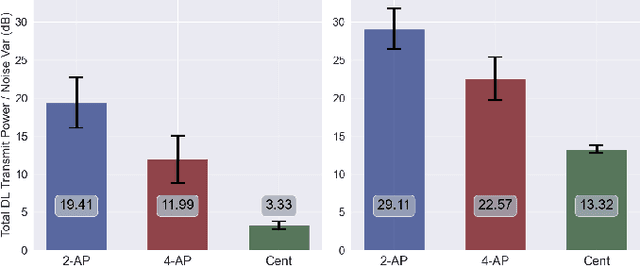
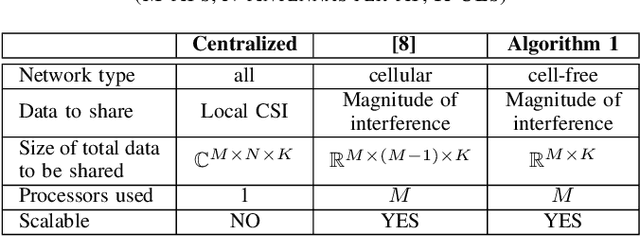
In cell-free massive MIMO systems with multiple distributed access points (APs) serving multiple users over the same time-frequency resources, downlink beamforming is done through spatial precoding. Precoding vectors can be optimally designed to use the minimum downlink transmit power while satisfying a quality-of-service requirement for each user. However, existing centralized solutions to beamforming optimization pose challenges such as high communication overhead and processing delay. On the other hand, distributed approaches either require data exchange over the network that scales with the number of antennas or solve the problem for cellular systems where every user is served by only one AP. In this paper, we formulate a multi-user beamforming optimization problem to minimize the total transmit power subject to per-user SINR requirements and propose a distributed optimization algorithm based on the alternating direction method of multipliers (ADMM) to solve it. In our method, every AP solves an iterative optimization problem using its local channel state information. APs only need to share a real-valued vector of interference terms with the size of the number of users. Through simulation results, we demonstrate that our proposed algorithm solves the optimization problem within tens of ADMM iterations and can effectively satisfy per-user SINR constraints.

Efficient Path Planning with Soft Homology Constraints

We study the problem of path planning with soft homology constraints on a surface topologically equivalent to a disk with punctures. Specifically, we propose an algorithm, named $\Hstar$, for the efficient computation of a path homologous to a user-provided reference path. We show that the algorithm can generate a suite of paths in distinct homology classes, from the overall shortest path to the shortest path homologous to the reference path, ordered both by path length and similarity to the reference path. Rollout is shown to improve the results produced by the algorithm. Experiments demonstrate that $\Hstar$ can be an efficient alternative to optimal methods, especially for configuration spaces with many obstacles.

An Optimal Transport Approach for Network Regression

We study the problem of network regression, where one is interested in how the topology of a network changes as a function of Euclidean covariates. We build upon recent developments in generalized regression models on metric spaces based on Fr\'echet means and propose a network regression method using the Wasserstein metric. We show that when representing graphs as multivariate Gaussian distributions, the network regression problem requires the computation of a Riemannian center of mass (i.e., Fr\'echet means). Fr\'echet means with non-negative weights translates into a barycenter problem and can be efficiently computed using fixed point iterations. Although the convergence guarantees of fixed-point iterations for the computation of Wasserstein affine averages remain an open problem, we provide evidence of convergence in a large number of synthetic and real-data scenarios. Extensive numerical results show that the proposed approach improves existing procedures by accurately accounting for graph size, topology, and sparsity in synthetic experiments. Additionally, real-world experiments using the proposed approach result in higher Coefficient of Determination ($R^{2}$) values and lower mean squared prediction error (MSPE), cementing improved prediction capabilities in practice.

A Moreau Envelope Approach for LQR Meta-Policy Estimation

We study the problem of policy estimation for the Linear Quadratic Regulator (LQR) in discrete-time linear time-invariant uncertain dynamical systems. We propose a Moreau Envelope-based surrogate LQR cost, built from a finite set of realizations of the uncertain system, to define a meta-policy efficiently adjustable to new realizations. Moreover, we design an algorithm to find an approximate first-order stationary point of the meta-LQR cost function. Numerical results show that the proposed approach outperforms naive averaging of controllers on new realizations of the linear system. We also provide empirical evidence that our method has better sample complexity than Model-Agnostic Meta-Learning (MAML) approaches.

Decentralized and Equitable Optimal Transport

This paper considers the decentralized (discrete) optimal transport (D-OT) problem. In this setting, a network of agents seeks to design a transportation plan jointly, where the cost function is the sum of privately held costs for each agent. We reformulate the D-OT problem as a constraint-coupled optimization problem and propose a single-loop decentralized algorithm with an iteration complexity of O(1/{\epsilon}) that matches existing centralized first-order approaches. Moreover, we propose the decentralized equitable optimal transport (DE-OT) problem. In DE-OT, in addition to cooperatively designing a transportation plan that minimizes transportation costs, agents seek to ensure equity in their individual costs. The iteration complexity of the proposed method to solve DE-OT is also O(1/{\epsilon}). This rate improves existing centralized algorithms, where the best iteration complexity obtained is O(1/{\epsilon}^2).

PIDformer: Transformer Meets Control Theory

In this work, we address two main shortcomings of transformer architectures: input corruption and rank collapse in their output representation. We unveil self-attention as an autonomous state-space model that inherently promotes smoothness in its solutions, leading to lower-rank outputs and diminished representation capacity. Moreover, the steady-state solution of the model is sensitive to input perturbations. We incorporate a Proportional-Integral-Derivative (PID) closed-loop feedback control system with a reference point into the model to improve robustness and representation capacity. This integration aims to preserve high-frequency details while bolstering model stability, rendering it more noise-resilient. The resulting controlled state-space model is theoretically proven robust and adept at addressing the rank collapse. Motivated by this control framework, we derive a novel class of transformers, PID-controlled Transformer (PIDformer), aimed at improving robustness and mitigating the rank-collapse issue inherent in softmax transformers. We empirically evaluate the model for advantages and robustness against baseline transformers across various practical tasks, including object classification, image segmentation, and language modeling.

Improving Denoising Diffusion Probabilistic Models via Exploiting Shared Representations

In this work, we address the challenge of multi-task image generation with limited data for denoising diffusion probabilistic models (DDPM), a class of generative models that produce high-quality images by reversing a noisy diffusion process. We propose a novel method, SR-DDPM, that leverages representation-based techniques from few-shot learning to effectively learn from fewer samples across different tasks. Our method consists of a core meta architecture with shared parameters, i.e., task-specific layers with exclusive parameters. By exploiting the similarity between diverse data distributions, our method can scale to multiple tasks without compromising the image quality. We evaluate our method on standard image datasets and show that it outperforms both unconditional and conditional DDPM in terms of FID and SSIM metrics.

Frequentist Guarantees of Distributed (Non)-Bayesian Inference

Motivated by the need to analyze large, decentralized datasets, distributed Bayesian inference has become a critical research area across multiple fields, including statistics, electrical engineering, and economics. This paper establishes Frequentist properties, such as posterior consistency, asymptotic normality, and posterior contraction rates, for the distributed (non-)Bayes Inference problem among agents connected via a communication network. Our results show that, under appropriate assumptions on the communication graph, distributed Bayesian inference retains parametric efficiency while enhancing robustness in uncertainty quantification. We also explore the trade-off between statistical efficiency and communication efficiency by examining how the design and size of the communication graph impact the posterior contraction rate. Furthermore, We extend our analysis to time-varying graphs and apply our results to exponential family models, distributed logistic regression, and decentralized detection models.

Adaptive Federated Learning with Auto-Tuned Clients

Federated learning (FL) is a distributed machine learning framework where the global model of a central server is trained via multiple collaborative steps by participating clients without sharing their data. While being a flexible framework, where the distribution of local data, participation rate, and computing power of each client can greatly vary, such flexibility gives rise to many new challenges, especially in the hyperparameter tuning on both the server and the client side. We propose $\Delta$-SGD, a simple step size rule for SGD that enables each client to use its own step size by adapting to the local smoothness of the function each client is optimizing. We provide theoretical and empirical results where the benefit of the client adaptivity is shown in various FL scenarios. In particular, our proposed method achieves TOP-1 accuracy in 73% and TOP-2 accuracy in 100% of the experiments considered without additional tuning.

On First-Order Meta-Reinforcement Learning with Moreau Envelopes

Meta-Reinforcement Learning (MRL) is a promising framework for training agents that can quickly adapt to new environments and tasks. In this work, we study the MRL problem under the policy gradient formulation, where we propose a novel algorithm that uses Moreau envelope surrogate regularizers to jointly learn a meta-policy that is adjustable to the environment of each individual task. Our algorithm, called Moreau Envelope Meta-Reinforcement Learning (MEMRL), learns a meta-policy that can adapt to a distribution of tasks by efficiently updating the policy parameters using a combination of gradient-based optimization and Moreau Envelope regularization. Moreau Envelopes provide a smooth approximation of the policy optimization problem, which enables us to apply standard optimization techniques and converge to an appropriate stationary point. We provide a detailed analysis of the MEMRL algorithm, where we show a sublinear convergence rate to a first-order stationary point for non-convex policy gradient optimization. We finally show the effectiveness of MEMRL on a multi-task 2D-navigation problem.