An Analytical and Experimental Study of Distributed Uplink Beamforming in the Presence of Carrier Frequency Offsets

Realizing distributed multi-user beamforming (D-MUBF) in time division duplex (TDD)-based multi-user MIMO (MU-MIMO) systems faces significant challenges. One of the most fundamental challenges is achieving accurate over-the-air (OTA) timing and frequency synchronization among distributed access points (APs), particularly due to residual frequency offsets caused by local oscillator (LO) drifts. Despite decades of research on synchronization for MU-MIMO, there are only a few experimental studies that evaluate D-MUBF techniques under imperfect frequency synchronization among distributed antennas. This paper presents an analytical and experimental assessment of D-MUBF methods in the presence of frequency synchronization errors. We provide closed-form expressions for signal-to-interference-plus-noise ratio (SINR) as a function of channel characteristics and statistical properties of carrier frequency offset (CFO) among AP antennas. In addition, through experimental evaluations conducted with the RENEW massive MIMO testbed, we collected comprehensive datasets across various experimental scenarios. These datasets comprise uplink pilot samples for channel and CFO estimation, in addition to uplink multi-user data intended for analyzing D-MUBF techniques. By examining these datasets, we assess the performance of D-MUBF in the presence of CFO and compare the analytical predictions with empirical measurements. Furthermore, we make the datasets publicly available and provide insights on utilizing them for future research endeavors.

ADMM for Downlink Beamforming in Cell-Free Massive MIMO Systems

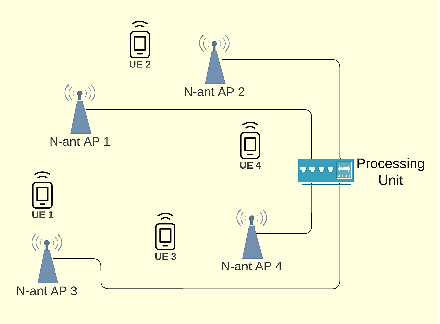
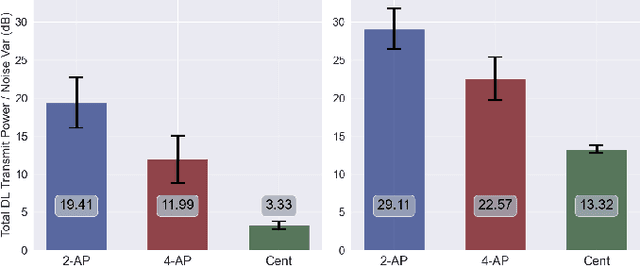
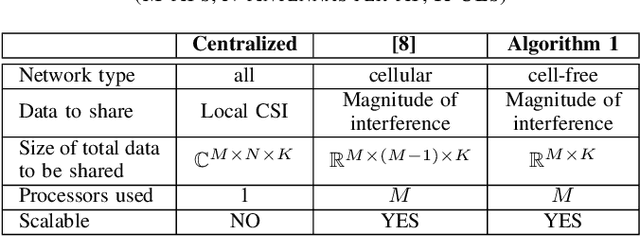
In cell-free massive MIMO systems with multiple distributed access points (APs) serving multiple users over the same time-frequency resources, downlink beamforming is done through spatial precoding. Precoding vectors can be optimally designed to use the minimum downlink transmit power while satisfying a quality-of-service requirement for each user. However, existing centralized solutions to beamforming optimization pose challenges such as high communication overhead and processing delay. On the other hand, distributed approaches either require data exchange over the network that scales with the number of antennas or solve the problem for cellular systems where every user is served by only one AP. In this paper, we formulate a multi-user beamforming optimization problem to minimize the total transmit power subject to per-user SINR requirements and propose a distributed optimization algorithm based on the alternating direction method of multipliers (ADMM) to solve it. In our method, every AP solves an iterative optimization problem using its local channel state information. APs only need to share a real-valued vector of interference terms with the size of the number of users. Through simulation results, we demonstrate that our proposed algorithm solves the optimization problem within tens of ADMM iterations and can effectively satisfy per-user SINR constraints.

An Introduction to Complex Random Tensors

This work considers the notion of random tensors and reviews some fundamental concepts in statistics when applied to a tensor based data or signal. In several engineering fields such as Communications, Signal Processing, Machine learning, and Control systems, the concepts of linear algebra combined with random variables have been indispensable tools. With the evolution of these subjects to multi-domain communication systems, multi-way signal processing, high dimensional data analysis, and multi-linear systems theory, there is a need to bring in multi-linear algebra equipped with the notion of random tensors. Also, since several such application areas deal with complex-valued entities, it is imperative to study this subject from a complex random tensor perspective, which is the focus of this paper. Using tools from multi-linear algebra, we characterize statistical properties of complex random tensors, both proper and improper, study various correlation structures, and fundamentals of tensor valued random processes. Furthermore, the asymptotic distribution of various tensor eigenvalue and singular value definitions is also considered, which is used for the study of spiked real tensor models that deals with recovery of low rank tensor signals perturbed by noise. This paper aims to provide an overview of the state of the art in random tensor theory of both complex and real valued tensors, for the purpose of enabling its application in engineering and applied science.