Completion of partial structures using Patterson maps with the CrysFormer machine learning model

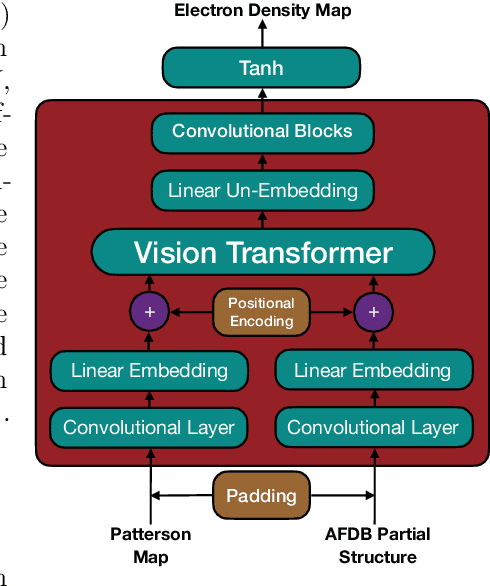
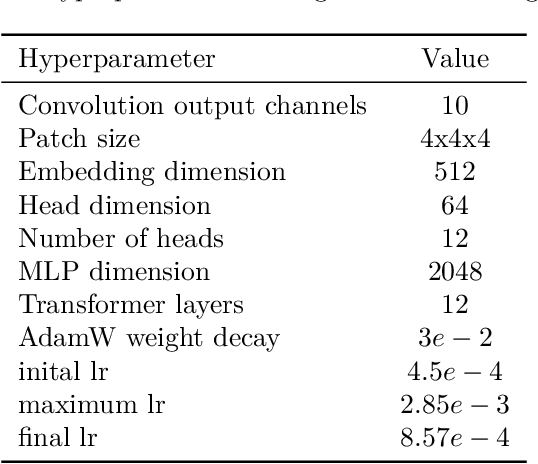
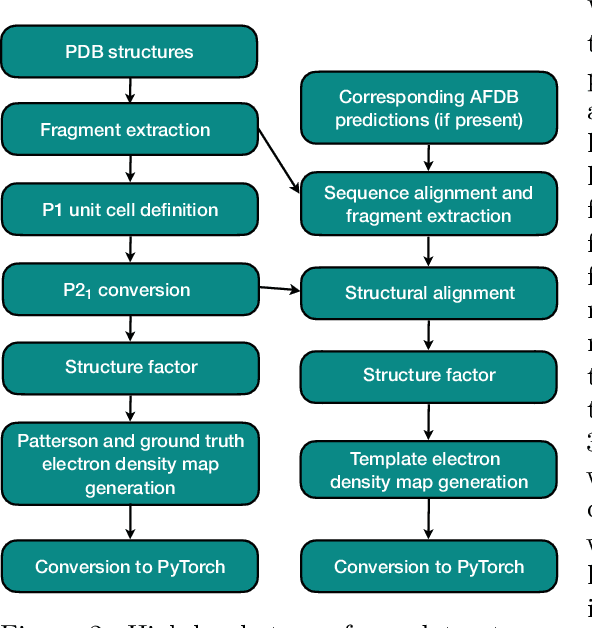
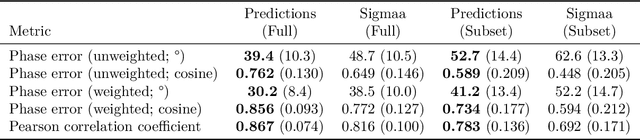
Protein structure determination has long been one of the primary challenges of structural biology, to which deep machine learning (ML)-based approaches have increasingly been applied. However, these ML models generally do not incorporate the experimental measurements directly, such as X-ray crystallographic diffraction data. To this end, we explore an approach that more tightly couples these traditional crystallographic and recent ML-based methods, by training a hybrid 3-d vision transformer and convolutional network on inputs from both domains. We make use of two distinct input constructs / Patterson maps, which are directly obtainable from crystallographic data, and ``partial structure'' template maps derived from predicted structures deposited in the AlphaFold Protein Structure Database with subsequently omitted residues. With these, we predict electron density maps that are then post-processed into atomic models through standard crystallographic refinement processes. Introducing an initial dataset of small protein fragments taken from Protein Data Bank entries and placing them in hypothetical crystal settings, we demonstrate that our method is effective at both improving the phases of the crystallographic structure factors and completing the regions missing from partial structure templates, as well as improving the agreement of the electron density maps with the ground truth atomic structures.

TwIST: Rigging the Lottery in Transformers with Independent Subnetwork Training

We introduce TwIST, a distributed training framework for efficient large language model (LLM) sparsification. TwIST trains multiple subnetworks in parallel, periodically aggregates their parameters, and resamples new subnetworks during training. This process identifies high-quality subnetworks ("golden tickets") without requiring post-training procedures such as calibration or Hessian-based recovery. As a result, TwIST enables zero-cost pruning at deployment time while achieving perplexity competitive with state-of-the-art post-training sparsification methods. The benefits are most pronounced under aggressive sparsity (e.g., 50%+), where TwIST significantly outperforms baseline methods; for example, reaching 23.14 PPL compared to 31.64 for the closest prior approach. Unlike unstructured pruning, TwIST produces structured, dense matrices that offer practical inference speedups and memory reductions on commodity hardware (e.g., CPUs) that do not support efficient sparse computation. TwIST provides an efficient training-time path to deployable sparse LLMs without additional fine-tuning or recovery overhead.

Three Birds with One Stone: Improving Performance, Convergence, and System Throughput with Nest

Variational quantum algorithms (VQAs) have the potential to demonstrate quantum utility on near-term quantum computers. However, these algorithms often get executed on the highest-fidelity qubits and computers to achieve the best performance, causing low system throughput. Recent efforts have shown that VQAs can be run on low-fidelity qubits initially and high-fidelity qubits later on to still achieve good performance. We take this effort forward and show that carefully varying the qubit fidelity map of the VQA over its execution using our technique, Nest, does not just (1) improve performance (i.e., help achieve close to optimal results), but also (2) lead to faster convergence. We also use Nest to co-locate multiple VQAs concurrently on the same computer, thus (3) increasing the system throughput, and therefore, balancing and optimizing three conflicting metrics simultaneously.

Guided by the Experts: Provable Feature Learning Dynamic of Soft-Routed Mixture-of-Experts

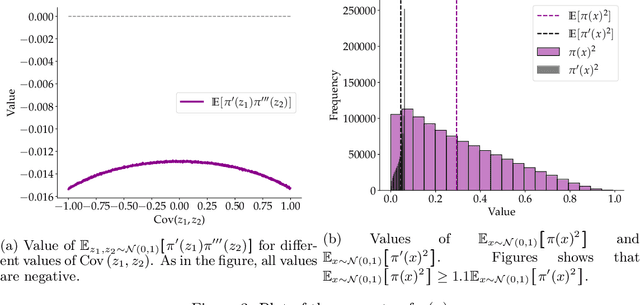
Mixture-of-Experts (MoE) architectures have emerged as a cornerstone of modern AI systems. In particular, MoEs route inputs dynamically to specialized experts whose outputs are aggregated through weighted summation. Despite their widespread application, theoretical understanding of MoE training dynamics remains limited to either separate expert-router optimization or only top-1 routing scenarios with carefully constructed datasets. This paper advances MoE theory by providing convergence guarantees for joint training of soft-routed MoE models with non-linear routers and experts in a student-teacher framework. We prove that, with moderate over-parameterization, the student network undergoes a feature learning phase, where the router's learning process is ``guided'' by the experts, that recovers the teacher's parameters. Moreover, we show that a post-training pruning can effectively eliminate redundant neurons, followed by a provably convergent fine-tuning process that reaches global optimality. To our knowledge, our analysis is the first to bring novel insights in understanding the optimization landscape of the MoE architecture.

One Rank at a Time: Cascading Error Dynamics in Sequential Learning

Sequential learning -- where complex tasks are broken down into simpler, hierarchical components -- has emerged as a paradigm in AI. This paper views sequential learning through the lens of low-rank linear regression, focusing specifically on how errors propagate when learning rank-1 subspaces sequentially. We present an analysis framework that decomposes the learning process into a series of rank-1 estimation problems, where each subsequent estimation depends on the accuracy of previous steps. Our contribution is a characterization of the error propagation in this sequential process, establishing bounds on how errors -- e.g., due to limited computational budgets and finite precision -- affect the overall model accuracy. We prove that these errors compound in predictable ways, with implications for both algorithmic design and stability guarantees.

Exploring How LLMs Capture and Represent Domain-Specific Knowledge

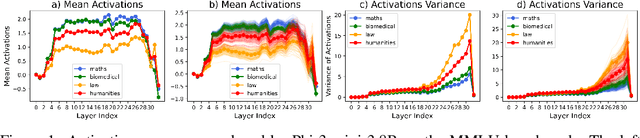
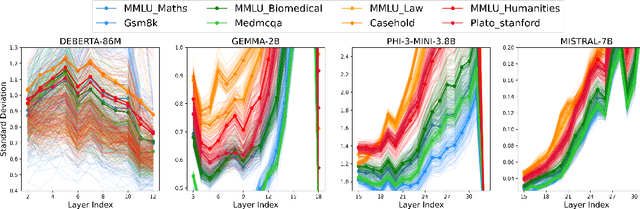
We study whether Large Language Models (LLMs) inherently capture domain-specific nuances in natural language. Our experiments probe the domain sensitivity of LLMs by examining their ability to distinguish queries from different domains using hidden states generated during the prefill phase. We reveal latent domain-related trajectories that indicate the model's internal recognition of query domains. We also study the robustness of these domain representations to variations in prompt styles and sources. Our approach leverages these representations for model selection, mapping the LLM that best matches the domain trace of the input query (i.e., the model with the highest performance on similar traces). Our findings show that LLMs can differentiate queries for related domains, and that the fine-tuned model is not always the most accurate. Unlike previous work, our interpretations apply to both closed and open-ended generative tasks

Quantum EigenGame for excited state calculation

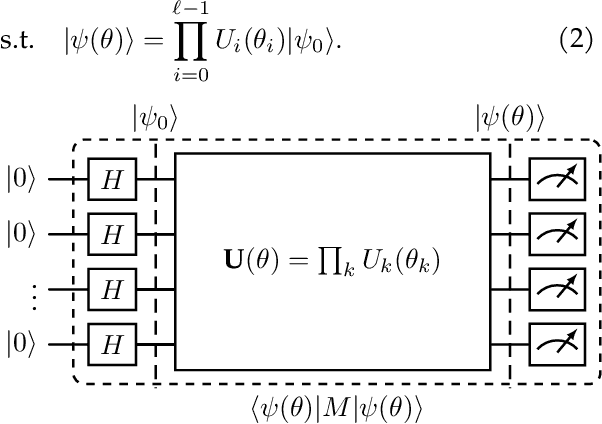
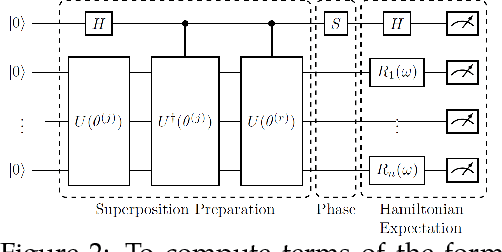
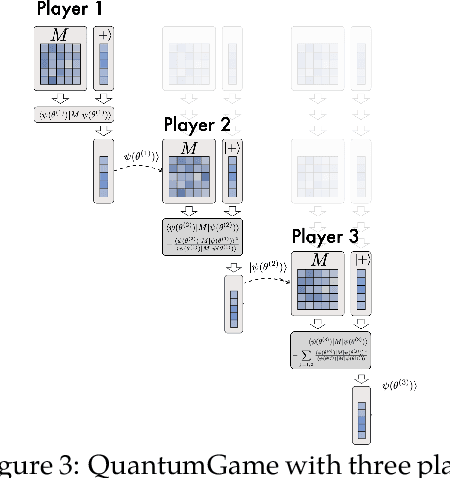
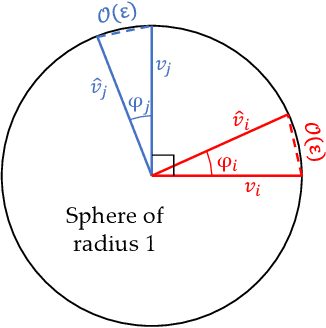
Computing the excited states of a given Hamiltonian is computationally hard for large systems, but methods that do so using quantum computers scale tractably. This problem is equivalent to the PCA problem where we are interested in decomposing a matrix into a collection of principal components. Classically, PCA is a well-studied problem setting, for which both centralized and distributed approaches have been developed. On the distributed side, one recent approach is that of EigenGame, a game-theoretic approach to finding eigenvectors where each eigenvector reaches a Nash equilibrium either sequentially or in parallel. With this work, we extend the EigenGame algorithm for both a $0^\text{th}$-order approach and for quantum computers, and harness the framework that quantum computing provides in computing excited states. Results show that using the Quantum EigenGame allows us to converge to excited states of a given Hamiltonian without the need of a deflation step. We also develop theory on error accumulation for finite-differences and parameterized approaches.

Unveiling Hidden Pivotal Players with GoalNet: A GNN-Based Soccer Player Evaluation System

Soccer analysis tools emphasize metrics such as expected goals, leading to an overrepresentation of attacking players' contributions and overlooking players who facilitate ball control and link attacks. Examples include Rodri from Manchester City and Palhinha who just transferred to Bayern Munich. To address this bias, we aim to identify players with pivotal roles in a soccer team, incorporating both spatial and temporal features. In this work, we introduce a GNN-based framework that assigns individual credit for changes in expected threat (xT), thus capturing overlooked yet vital contributions in soccer. Our pipeline encodes both spatial and temporal features in event-centric graphs, enabling fair attribution of non-scoring actions such as defensive or transitional plays. We incorporate centrality measures into the learned player embeddings, ensuring that ball-retaining defenders and defensive midfielders receive due recognition for their overall impact. Furthermore, we explore diverse GNN variants-including Graph Attention Networks and Transformer-based models-to handle long-range dependencies and evolving match contexts, discussing their relative performance and computational complexity. Experiments on real match data confirm the robustness of our approach in highlighting pivotal roles that traditional attacking metrics typically miss, underscoring the model's utility for more comprehensive soccer analytics.

Provable Model-Parallel Distributed Principal Component Analysis with Parallel Deflation

We study a distributed Principal Component Analysis (PCA) framework where each worker targets a distinct eigenvector and refines its solution by updating from intermediate solutions provided by peers deemed as "superior". Drawing intuition from the deflation method in centralized eigenvalue problems, our approach breaks the sequential dependency in the deflation steps and allows asynchronous updates of workers, while incurring only a small communication cost. To our knowledge, a gap in the literature -- the theoretical underpinning of such distributed, dynamic interactions among workers -- has remained unaddressed. This paper offers a theoretical analysis explaining why, how, and when these intermediate, hierarchical updates lead to practical and provable convergence in distributed environments. Despite being a theoretical work, our prototype implementation demonstrates that such a distributed PCA algorithm converges effectively and in scalable way: through experiments, our proposed framework offers comparable performance to EigenGame-$\mu$, the state-of-the-art model-parallel PCA solver.

A Catalyst Framework for the Quantum Linear System Problem via the Proximal Point Algorithm

Solving systems of linear equations is a fundamental problem, but it can be computationally intensive for classical algorithms in high dimensions. Existing quantum algorithms can achieve exponential speedups for the quantum linear system problem (QLSP) in terms of the problem dimension, but even such a theoretical advantage is bottlenecked by the condition number of the coefficient matrix. In this work, we propose a new quantum algorithm for QLSP inspired by the classical proximal point algorithm (PPA). Our proposed method can be viewed as a meta-algorithm that allows inverting a modified matrix via an existing \texttt{QLSP\_solver}, thereby directly approximating the solution vector instead of approximating the inverse of the coefficient matrix. By carefully choosing the step size $\eta$, the proposed algorithm can effectively precondition the linear system to mitigate the dependence on condition numbers that hindered the applicability of previous approaches.