Cruz Barnum
On the Error-Propagation of Inexact Deflation for Principal Component Analysis
Oct 06, 2023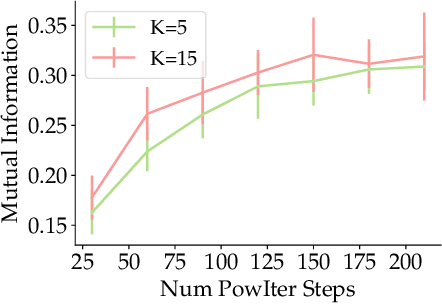
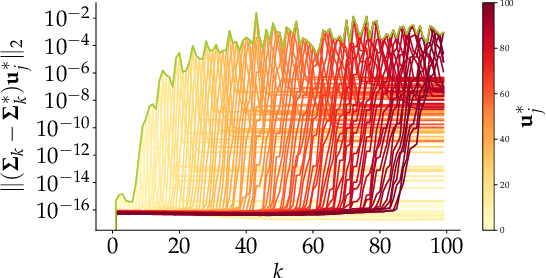
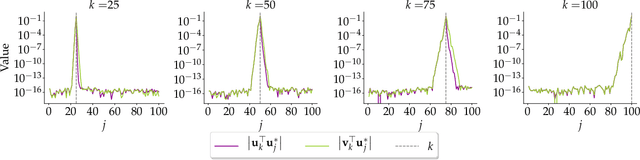
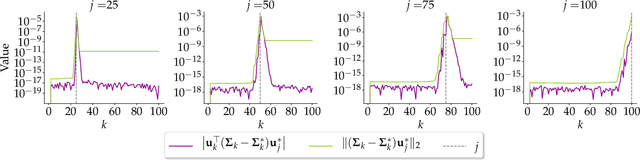
Abstract:Principal Component Analysis (PCA) is a popular tool in data analysis, especially when the data is high-dimensional. PCA aims to find subspaces, spanned by the so-called \textit{principal components}, that best explain the variance in the dataset. The deflation method is a popular meta-algorithm -- used to discover such subspaces -- that sequentially finds individual principal components, starting from the most important one and working its way towards the less important ones. However, due to its sequential nature, the numerical error introduced by not estimating principal components exactly -- e.g., due to numerical approximations through this process -- propagates, as deflation proceeds. To the best of our knowledge, this is the first work that mathematically characterizes the error propagation of the inexact deflation method, and this is the key contribution of this paper. We provide two main results: $i)$ when the sub-routine for finding the leading eigenvector is generic, and $ii)$ when power iteration is used as the sub-routine. In the latter case, the additional directional information from power iteration allows us to obtain a tighter error bound than the analysis of the sub-routine agnostic case. As an outcome, we provide explicit characterization on how the error progresses and affects subsequent principal component estimations for this fundamental problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge