Solving Hidden Monotone Variational Inequalities with Surrogate Losses

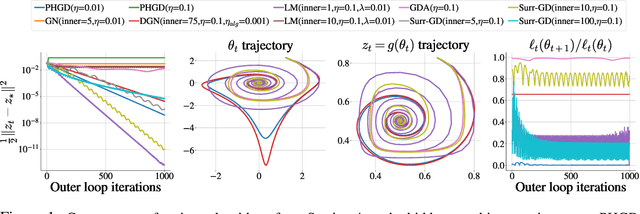
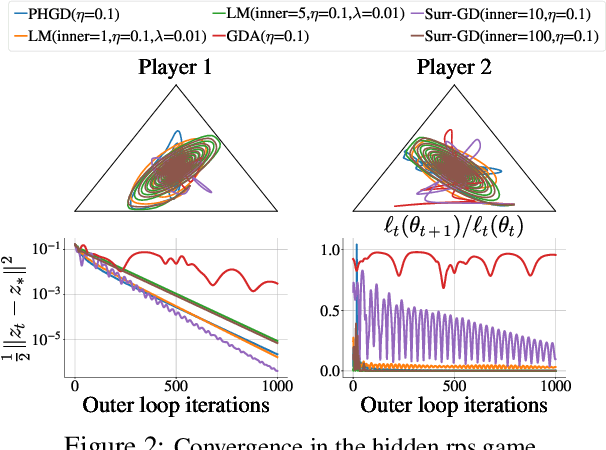
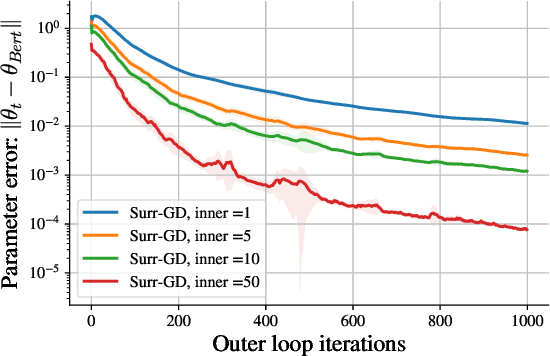
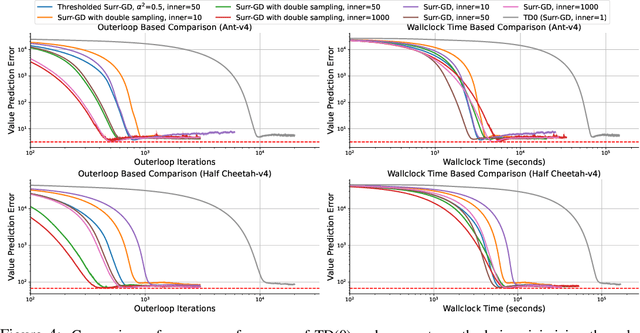
Deep learning has proven to be effective in a wide variety of loss minimization problems. However, many applications of interest, like minimizing projected Bellman error and min-max optimization, cannot be modelled as minimizing a scalar loss function but instead correspond to solving a variational inequality (VI) problem. This difference in setting has caused many practical challenges as naive gradient-based approaches from supervised learning tend to diverge and cycle in the VI case. In this work, we propose a principled surrogate-based approach compatible with deep learning to solve VIs. We show that our surrogate-based approach has three main benefits: (1) under assumptions that are realistic in practice (when hidden monotone structure is present, interpolation, and sufficient optimization of the surrogates), it guarantees convergence, (2) it provides a unifying perspective of existing methods, and (3) is amenable to existing deep learning optimizers like ADAM. Experimentally, we demonstrate our surrogate-based approach is effective in min-max optimization and minimizing projected Bellman error. Furthermore, in the deep reinforcement learning case, we propose a novel variant of TD(0) which is more compute and sample efficient.

A Catalyst Framework for the Quantum Linear System Problem via the Proximal Point Algorithm

Solving systems of linear equations is a fundamental problem, but it can be computationally intensive for classical algorithms in high dimensions. Existing quantum algorithms can achieve exponential speedups for the quantum linear system problem (QLSP) in terms of the problem dimension, but even such a theoretical advantage is bottlenecked by the condition number of the coefficient matrix. In this work, we propose a new quantum algorithm for QLSP inspired by the classical proximal point algorithm (PPA). Our proposed method can be viewed as a meta-algorithm that allows inverting a modified matrix via an existing \texttt{QLSP\_solver}, thereby directly approximating the solution vector instead of approximating the inverse of the coefficient matrix. By carefully choosing the step size $\eta$, the proposed algorithm can effectively precondition the linear system to mitigate the dependence on condition numbers that hindered the applicability of previous approaches.

On the Error-Propagation of Inexact Deflation for Principal Component Analysis

Principal Component Analysis (PCA) is a popular tool in data analysis, especially when the data is high-dimensional. PCA aims to find subspaces, spanned by the so-called \textit{principal components}, that best explain the variance in the dataset. The deflation method is a popular meta-algorithm -- used to discover such subspaces -- that sequentially finds individual principal components, starting from the most important one and working its way towards the less important ones. However, due to its sequential nature, the numerical error introduced by not estimating principal components exactly -- e.g., due to numerical approximations through this process -- propagates, as deflation proceeds. To the best of our knowledge, this is the first work that mathematically characterizes the error propagation of the inexact deflation method, and this is the key contribution of this paper. We provide two main results: $i)$ when the sub-routine for finding the leading eigenvector is generic, and $ii)$ when power iteration is used as the sub-routine. In the latter case, the additional directional information from power iteration allows us to obtain a tighter error bound than the analysis of the sub-routine agnostic case. As an outcome, we provide explicit characterization on how the error progresses and affects subsequent principal component estimations for this fundamental problem.

Adaptive Federated Learning with Auto-Tuned Clients

Federated learning (FL) is a distributed machine learning framework where the global model of a central server is trained via multiple collaborative steps by participating clients without sharing their data. While being a flexible framework, where the distribution of local data, participation rate, and computing power of each client can greatly vary, such flexibility gives rise to many new challenges, especially in the hyperparameter tuning on both the server and the client side. We propose $\Delta$-SGD, a simple step size rule for SGD that enables each client to use its own step size by adapting to the local smoothness of the function each client is optimizing. We provide theoretical and empirical results where the benefit of the client adaptivity is shown in various FL scenarios. In particular, our proposed method achieves TOP-1 accuracy in 73% and TOP-2 accuracy in 100% of the experiments considered without additional tuning.

Extragradient with Positive Momentum is Optimal for Games with Cross-Shaped Jacobian Spectrum

The extragradient method has recently gained increasing attention, due to its convergence behavior on smooth games. In $n$-player differentiable games, the eigenvalues of the Jacobian of the vector field are distributed on the complex plane, exhibiting more convoluted dynamics compared to classical (i.e., single player) minimization. In this work, we take a polynomial-based analysis of the extragradient with momentum for optimizing games with \emph{cross-shaped} Jacobian spectrum on the complex plane. We show two results. First, based on the hyperparameter setup, the extragradient with momentum exhibits three different modes of convergence: when the eigenvalues are distributed $i)$ on the real line, $ii)$ both on the real line along with complex conjugates, and $iii)$ only as complex conjugates. Then, we focus on the case $ii)$, i.e., when the eigenvalues of the Jacobian have \emph{cross-shaped} structure, as observed in training generative adversarial networks. For this problem class, we derive the optimal hyperparameters of the momentum extragradient method, and show that it achieves an accelerated convergence rate.

Local Stochastic Factored Gradient Descent for Distributed Quantum State Tomography

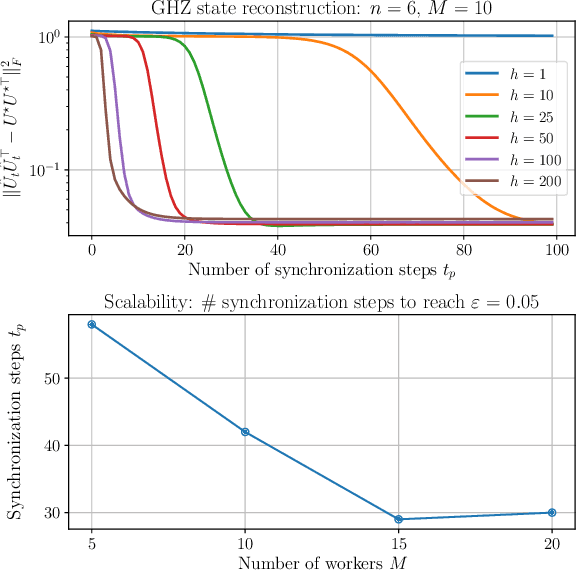
We propose a distributed Quantum State Tomography (QST) protocol, named Local Stochastic Factored Gradient Descent (Local SFGD), to learn the low-rank factor of a density matrix over a set of local machines. QST is the canonical procedure to characterize the state of a quantum system, which we formulate as a stochastic nonconvex smooth optimization problem. Physically, the estimation of a low-rank density matrix helps characterizing the amount of noise introduced by quantum computation. Theoretically, we prove the local convergence of Local SFGD for a general class of restricted strongly convex/smooth loss functions, i.e., Local SFGD converges locally to a small neighborhood of the global optimum at a linear rate with a constant step size, while it locally converges exactly at a sub-linear rate with diminishing step sizes. With a proper initialization, local convergence results imply global convergence. We validate our theoretical findings with numerical simulations of QST on the Greenberger-Horne-Zeilinger (GHZ) state.

Convergence and Stability of the Stochastic Proximal Point Algorithm with Momentum

Stochastic gradient descent with momentum (SGDM) is the dominant algorithm in many optimization scenarios, including convex optimization instances and non-convex neural network training. Yet, in the stochastic setting, momentum interferes with gradient noise, often leading to specific step size and momentum choices in order to guarantee convergence, set aside acceleration. Proximal point methods, on the other hand, have gained much attention due to their numerical stability and elasticity against imperfect tuning. Their stochastic accelerated variants though have received limited attention: how momentum interacts with the stability of (stochastic) proximal point methods remains largely unstudied. To address this, we focus on the convergence and stability of the stochastic proximal point algorithm with momentum (SPPAM), and show that SPPAM allows a faster linear convergence rate compared to stochastic proximal point algorithm (SPPA) with a better contraction factor, under proper hyperparameter tuning. In terms of stability, we show that SPPAM depends on problem constants more favorably than SGDM, allowing a wider range of step size and momentum that lead to convergence.

Provably Efficient Lottery Ticket Discovery

The lottery ticket hypothesis (LTH) claims that randomly-initialized, dense neural networks contain (sparse) subnetworks that, when trained an equal amount in isolation, can match the dense network's performance. Although LTH is useful for discovering efficient network architectures, its three-step process -- pre-training, pruning, and re-training -- is computationally expensive, as the dense model must be fully pre-trained. Luckily, "early-bird" tickets can be discovered within neural networks that are minimally pre-trained, allowing for the creation of efficient, LTH-inspired training procedures. Yet, no theoretical foundation of this phenomenon exists. We derive an analytical bound for the number of pre-training iterations that must be performed for a winning ticket to be discovered, thus providing a theoretical understanding of when and why such early-bird tickets exist. By adopting a greedy forward selection pruning strategy, we directly connect the pruned network's performance to the loss of the dense network from which it was derived, revealing a threshold in the number of pre-training iterations beyond which high-performing subnetworks are guaranteed to exist. We demonstrate the validity of our theoretical results across a variety of architectures and datasets, including multi-layer perceptrons (MLPs) trained on MNIST and several deep convolutional neural network (CNN) architectures trained on CIFAR10 and ImageNet.

Momentum-inspired Low-Rank Coordinate Descent for Diagonally Constrained SDPs

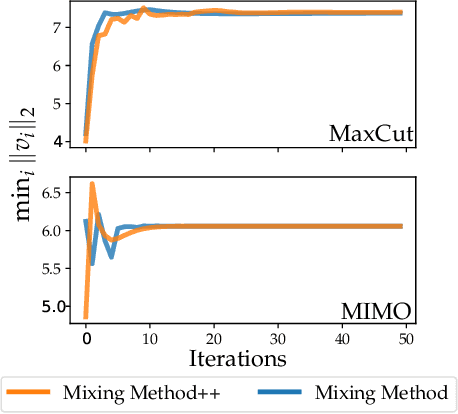
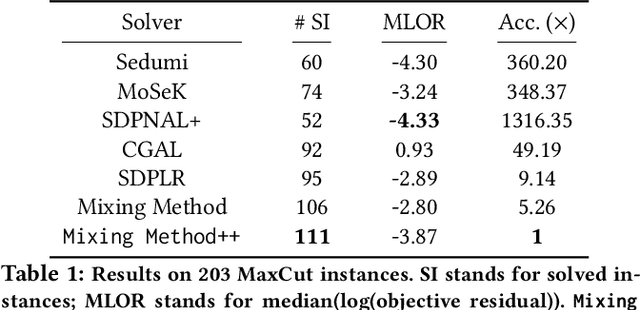
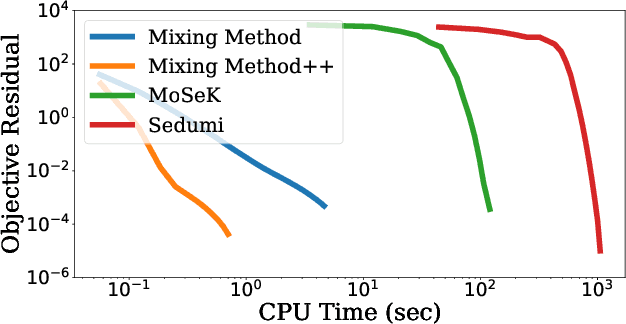
We present a novel, practical, and provable approach for solving diagonally constrained semi-definite programming (SDP) problems at scale using accelerated non-convex programming. Our algorithm non-trivially combines acceleration motions from convex optimization with coordinate power iteration and matrix factorization techniques. The algorithm is extremely simple to implement, and adds only a single extra hyperparameter -- momentum. We prove that our method admits local linear convergence in the neighborhood of the optimum and always converges to a first-order critical point. Experimentally, we showcase the merits of our method on three major application domains: MaxCut, MaxSAT, and MIMO signal detection. In all cases, our methodology provides significant speedups over non-convex and convex SDP solvers -- 5X faster than state-of-the-art non-convex solvers, and 9 to 10^3 X faster than convex SDP solvers -- with comparable or improved solution quality.

Fast quantum state reconstruction via accelerated non-convex programming

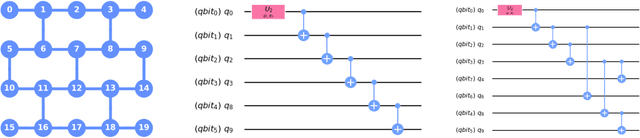
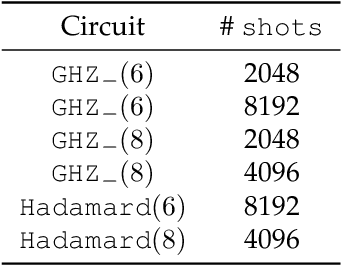
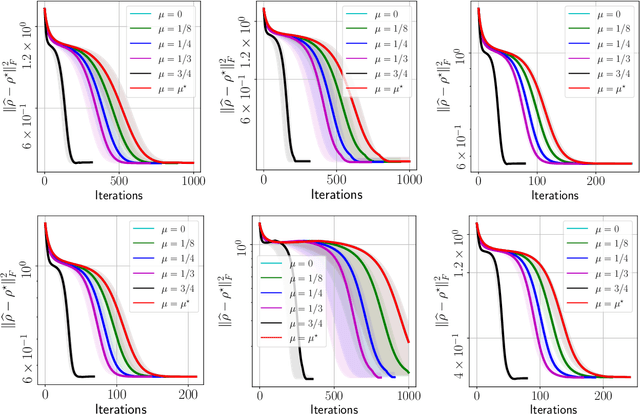
We propose a new quantum state reconstruction method that combines ideas from compressed sensing, non-convex optimization, and acceleration methods. The algorithm, called Momentum-Inspired Factored Gradient Descent (\texttt{MiFGD}), extends the applicability of quantum tomography for larger systems. Despite being a non-convex method, \texttt{MiFGD} converges \emph{provably} to the true density matrix at a linear rate, in the absence of experimental and statistical noise, and under common assumptions. With this manuscript, we present the method, prove its convergence property and provide Frobenius norm bound guarantees with respect to the true density matrix. From a practical point of view, we benchmark the algorithm performance with respect to other existing methods, in both synthetic and real experiments performed on an IBM's quantum processing unit. We find that the proposed algorithm performs orders of magnitude faster than state of the art approaches, with the same or better accuracy. In both synthetic and real experiments, we observed accurate and robust reconstruction, despite experimental and statistical noise in the tomographic data. Finally, we provide a ready-to-use code for state tomography of multi-qubit systems.