Solving Hidden Monotone Variational Inequalities with Surrogate Losses
Paper and Code
Nov 07, 2024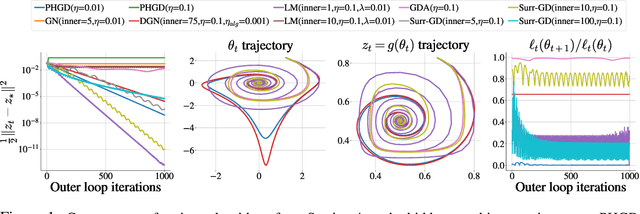
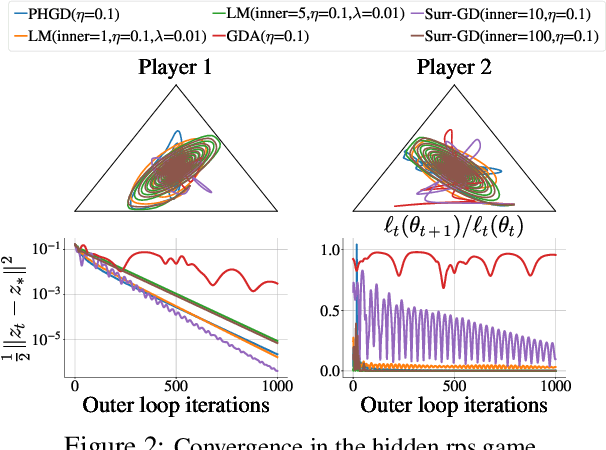
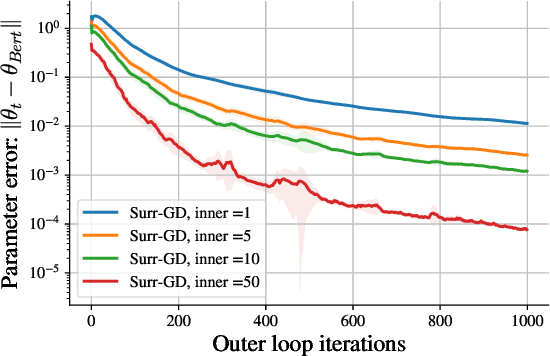
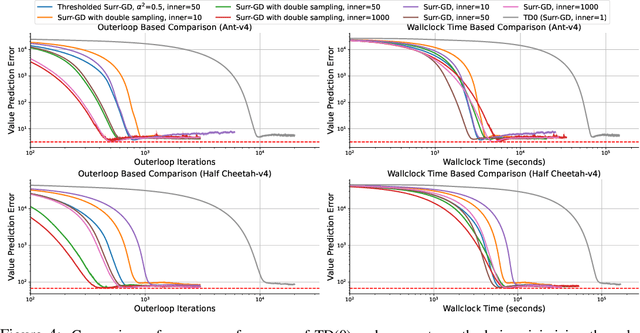
Deep learning has proven to be effective in a wide variety of loss minimization problems. However, many applications of interest, like minimizing projected Bellman error and min-max optimization, cannot be modelled as minimizing a scalar loss function but instead correspond to solving a variational inequality (VI) problem. This difference in setting has caused many practical challenges as naive gradient-based approaches from supervised learning tend to diverge and cycle in the VI case. In this work, we propose a principled surrogate-based approach compatible with deep learning to solve VIs. We show that our surrogate-based approach has three main benefits: (1) under assumptions that are realistic in practice (when hidden monotone structure is present, interpolation, and sufficient optimization of the surrogates), it guarantees convergence, (2) it provides a unifying perspective of existing methods, and (3) is amenable to existing deep learning optimizers like ADAM. Experimentally, we demonstrate our surrogate-based approach is effective in min-max optimization and minimizing projected Bellman error. Furthermore, in the deep reinforcement learning case, we propose a novel variant of TD(0) which is more compute and sample efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge