Ioannis Mitliagkas
Adaptive Batch Sizes Using Non-Euclidean Gradient Noise Scales for Stochastic Sign and Spectral Descent
Feb 03, 2026Abstract:To maximize hardware utilization, modern machine learning systems typically employ large constant or manually tuned batch size schedules, relying on heuristics that are brittle and costly to tune. Existing adaptive strategies based on gradient noise scale (GNS) offer a principled alternative. However, their assumption of SGD's Euclidean geometry creates a fundamental mismatch with popular optimizers based on generalized norms, such as signSGD / Signum ($\ell_\infty$) and stochastic spectral descent (specSGD) / Muon ($\mathcal{S}_\infty$). In this work, we derive gradient noise scales for signSGD and specSGD that naturally emerge from the geometry of their respective dual norms. To practically estimate these non-Euclidean metrics, we propose an efficient variance estimation procedure that leverages the local mini-batch gradients on different ranks in distributed data-parallel systems. Our experiments demonstrate that adaptive batch size strategies using non-Euclidean GNS enable us to match the validation loss of constant-batch baselines while reducing training steps by up to 66% for Signum and Muon on a 160 million parameter Llama model.
Revisiting Generalization Measures Beyond IID: An Empirical Study under Distributional Shift
Feb 02, 2026Abstract:Generalization remains a central yet unresolved challenge in deep learning, particularly the ability to predict a model's performance beyond its training distribution using quantities available prior to test-time evaluation. Building on the large-scale study of Jiang et al. (2020). and concerns by Dziugaite et al. (2020). about instability across training configurations, we benchmark the robustness of generalization measures beyond IID regime. We train small-to-medium models over 10,000 hyperparameter configurations and evaluate more than 40 measures computable from the trained model and the available training data alone. We significantly broaden the experimental scope along multiple axes: (i) extending the evaluation beyond the standard IID setting to include benchmarking for robustness across diverse distribution shifts, (ii) evaluating multiple architectures and training recipes, and (iii) newly incorporating calibration- and information-criteria-based measures to assess their alignment with both IID and OOD generalization. We find that distribution shifts can substantially alter the predictive performance of many generalization measures, while a smaller subset remains comparatively stable across settings.
Pseudo-Asynchronous Local SGD: Robust and Efficient Data-Parallel Training
Apr 25, 2025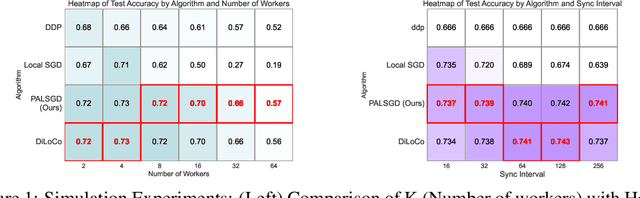
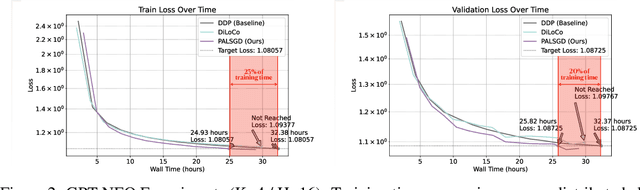
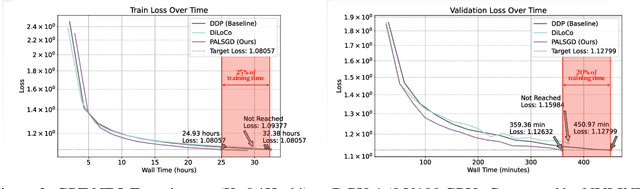
Abstract:Following AI scaling trends, frontier models continue to grow in size and continue to be trained on larger datasets. Training these models requires huge investments in exascale computational resources, which has in turn driven development of distributed deep learning methods. Data parallelism is an essential approach to speed up training, but it requires frequent global communication between workers, which can bottleneck training at the largest scales. In this work, we propose a method called Pseudo-Asynchronous Local SGD (PALSGD) to improve the efficiency of data-parallel training. PALSGD is an extension of Local SGD (Stich, 2018) and DiLoCo (Douillard et al., 2023), designed to further reduce communication frequency by introducing a pseudo-synchronization mechanism. PALSGD allows the use of longer synchronization intervals compared to standard Local SGD. Despite the reduced communication frequency, the pseudo-synchronization approach ensures that model consistency is maintained, leading to performance results comparable to those achieved with more frequent synchronization. Furthermore, we provide a theoretical analysis of PALSGD, establishing its convergence and deriving its convergence rate. This analysis offers insights into the algorithm's behavior and performance guarantees. We evaluated PALSGD on image classification and language modeling tasks. Our results show that PALSGD achieves better performance in less time compared to existing methods like Distributed Data Parallel (DDP), and DiLoCo. Notably, PALSGD trains 18.4% faster than DDP on ImageNet-1K with ResNet-50, 24.4% faster than DDP on TinyStories with GPT-Neo125M, and 21.1% faster than DDP on TinyStories with GPT-Neo-8M.
Learning to Defer for Causal Discovery with Imperfect Experts
Feb 18, 2025
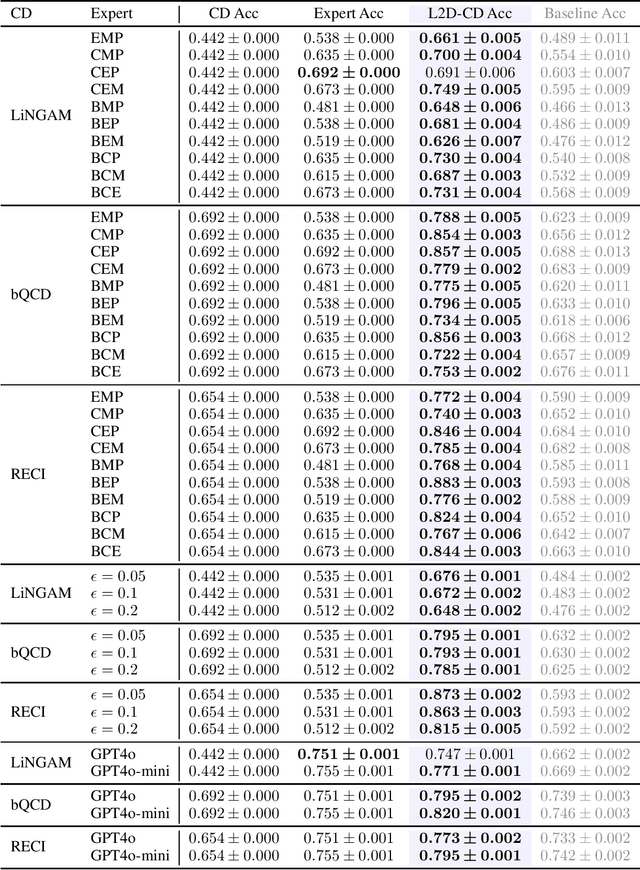
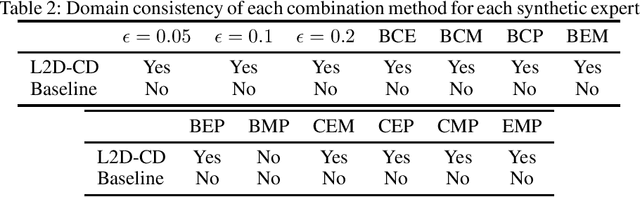
Abstract:Integrating expert knowledge, e.g. from large language models, into causal discovery algorithms can be challenging when the knowledge is not guaranteed to be correct. Expert recommendations may contradict data-driven results, and their reliability can vary significantly depending on the domain or specific query. Existing methods based on soft constraints or inconsistencies in predicted causal relationships fail to account for these variations in expertise. To remedy this, we propose L2D-CD, a method for gauging the correctness of expert recommendations and optimally combining them with data-driven causal discovery results. By adapting learning-to-defer (L2D) algorithms for pairwise causal discovery (CD), we learn a deferral function that selects whether to rely on classical causal discovery methods using numerical data or expert recommendations based on textual meta-data. We evaluate L2D-CD on the canonical T\"ubingen pairs dataset and demonstrate its superior performance compared to both the causal discovery method and the expert used in isolation. Moreover, our approach identifies domains where the expert's performance is strong or weak. Finally, we outline a strategy for generalizing this approach to causal discovery on graphs with more than two variables, paving the way for further research in this area.
Performance Control in Early Exiting to Deploy Large Models at the Same Cost of Smaller Ones
Dec 26, 2024Abstract:Early Exiting (EE) is a promising technique for speeding up inference by adaptively allocating compute resources to data points based on their difficulty. The approach enables predictions to exit at earlier layers for simpler samples while reserving more computation for challenging ones. In this study, we first present a novel perspective on the EE approach, showing that larger models deployed with EE can achieve higher performance than smaller models while maintaining similar computational costs. As existing EE approaches rely on confidence estimation at each exit point, we further study the impact of overconfidence on the controllability of the compute-performance trade-off. We introduce Performance Control Early Exiting (PCEE), a method that enables accuracy thresholding by basing decisions not on a data point's confidence but on the average accuracy of samples with similar confidence levels from a held-out validation set. In our experiments, we show that PCEE offers a simple yet computationally efficient approach that provides better control over performance than standard confidence-based approaches, and allows us to scale up model sizes to yield performance gain while reducing the computational cost.
Solving Hidden Monotone Variational Inequalities with Surrogate Losses
Nov 07, 2024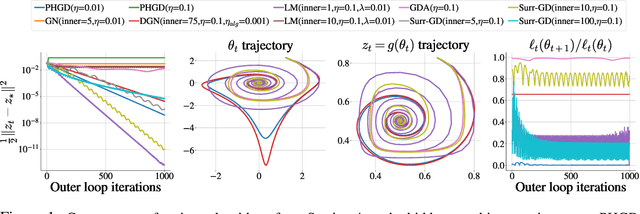
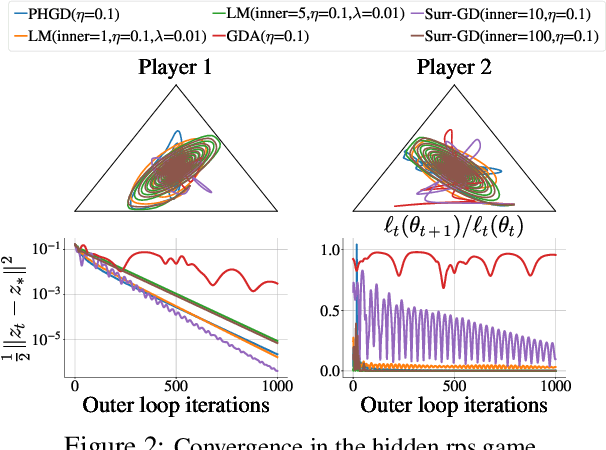
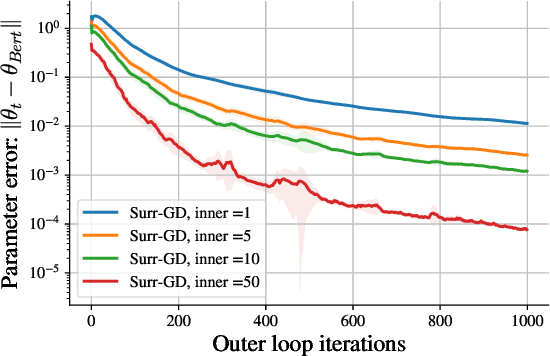
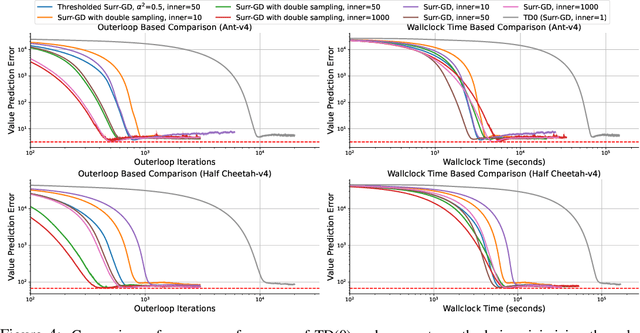
Abstract:Deep learning has proven to be effective in a wide variety of loss minimization problems. However, many applications of interest, like minimizing projected Bellman error and min-max optimization, cannot be modelled as minimizing a scalar loss function but instead correspond to solving a variational inequality (VI) problem. This difference in setting has caused many practical challenges as naive gradient-based approaches from supervised learning tend to diverge and cycle in the VI case. In this work, we propose a principled surrogate-based approach compatible with deep learning to solve VIs. We show that our surrogate-based approach has three main benefits: (1) under assumptions that are realistic in practice (when hidden monotone structure is present, interpolation, and sufficient optimization of the surrogates), it guarantees convergence, (2) it provides a unifying perspective of existing methods, and (3) is amenable to existing deep learning optimizers like ADAM. Experimentally, we demonstrate our surrogate-based approach is effective in min-max optimization and minimizing projected Bellman error. Furthermore, in the deep reinforcement learning case, we propose a novel variant of TD(0) which is more compute and sample efficient.
Understanding Adam Requires Better Rotation Dependent Assumptions
Oct 25, 2024



Abstract:Despite its widespread adoption, Adam's advantage over Stochastic Gradient Descent (SGD) lacks a comprehensive theoretical explanation. This paper investigates Adam's sensitivity to rotations of the parameter space. We demonstrate that Adam's performance in training transformers degrades under random rotations of the parameter space, indicating a crucial sensitivity to the choice of basis. This reveals that conventional rotation-invariant assumptions are insufficient to capture Adam's advantages theoretically. To better understand the rotation-dependent properties that benefit Adam, we also identify structured rotations that preserve or even enhance its empirical performance. We then examine the rotation-dependent assumptions in the literature, evaluating their adequacy in explaining Adam's behavior across various rotation types. This work highlights the need for new, rotation-dependent theoretical frameworks to fully understand Adam's empirical success in modern machine learning tasks.
Generating Tabular Data Using Heterogeneous Sequential Feature Forest Flow Matching
Oct 20, 2024



Abstract:Privacy and regulatory constraints make data generation vital to advancing machine learning without relying on real-world datasets. A leading approach for tabular data generation is the Forest Flow (FF) method, which combines Flow Matching with XGBoost. Despite its good performance, FF is slow and makes errors when treating categorical variables as one-hot continuous features. It is also highly sensitive to small changes in the initial conditions of the ordinary differential equation (ODE). To overcome these limitations, we develop Heterogeneous Sequential Feature Forest Flow (HS3F). Our method generates data sequentially (feature-by-feature), reducing the dependency on noisy initial conditions through the additional information from previously generated features. Furthermore, it generates categorical variables using multinomial sampling (from an XGBoost classifier) instead of flow matching, improving generation speed. We also use a Runge-Kutta 4th order (Rg4) ODE solver for improved performance over the Euler solver used in FF. Our experiments with 25 datasets reveal that HS3F produces higher quality and more diverse synthetic data than FF, especially for categorical variables. It also generates data 21-27 times faster for datasets with $\geq20%$ categorical variables. HS3F further demonstrates enhanced robustness to affine transformation in flow ODE initial conditions compared to FF. This study not only validates the HS3F but also unveils promising new strategies to advance generative models.
Compositional Risk Minimization
Oct 08, 2024



Abstract:In this work, we tackle a challenging and extreme form of subpopulation shift, which is termed compositional shift. Under compositional shifts, some combinations of attributes are totally absent from the training distribution but present in the test distribution. We model the data with flexible additive energy distributions, where each energy term represents an attribute, and derive a simple alternative to empirical risk minimization termed compositional risk minimization (CRM). We first train an additive energy classifier to predict the multiple attributes and then adjust this classifier to tackle compositional shifts. We provide an extensive theoretical analysis of CRM, where we show that our proposal extrapolates to special affine hulls of seen attribute combinations. Empirical evaluations on benchmark datasets confirms the improved robustness of CRM compared to other methods from the literature designed to tackle various forms of subpopulation shifts.
Are we making progress in unlearning? Findings from the first NeurIPS unlearning competition
Jun 13, 2024



Abstract:We present the findings of the first NeurIPS competition on unlearning, which sought to stimulate the development of novel algorithms and initiate discussions on formal and robust evaluation methodologies. The competition was highly successful: nearly 1,200 teams from across the world participated, and a wealth of novel, imaginative solutions with different characteristics were contributed. In this paper, we analyze top solutions and delve into discussions on benchmarking unlearning, which itself is a research problem. The evaluation methodology we developed for the competition measures forgetting quality according to a formal notion of unlearning, while incorporating model utility for a holistic evaluation. We analyze the effectiveness of different instantiations of this evaluation framework vis-a-vis the associated compute cost, and discuss implications for standardizing evaluation. We find that the ranking of leading methods remains stable under several variations of this framework, pointing to avenues for reducing the cost of evaluation. Overall, our findings indicate progress in unlearning, with top-performing competition entries surpassing existing algorithms under our evaluation framework. We analyze trade-offs made by different algorithms and strengths or weaknesses in terms of generalizability to new datasets, paving the way for advancing both benchmarking and algorithm development in this important area.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge