What do near-optimal learning rate schedules look like?

A basic unanswered question in neural network training is: what is the best learning rate schedule shape for a given workload? The choice of learning rate schedule is a key factor in the success or failure of the training process, but beyond having some kind of warmup and decay, there is no consensus on what makes a good schedule shape. To answer this question, we designed a search procedure to find the best shapes within a parameterized schedule family. Our approach factors out the schedule shape from the base learning rate, which otherwise would dominate cross-schedule comparisons. We applied our search procedure to a variety of schedule families on three workloads: linear regression, image classification on CIFAR-10, and small-scale language modeling on Wikitext103. We showed that our search procedure indeed generally found near-optimal schedules. We found that warmup and decay are robust features of good schedules, and that commonly used schedule families are not optimal on these workloads. Finally, we explored how the outputs of our shape search depend on other optimization hyperparameters, and found that weight decay can have a strong effect on the optimal schedule shape. To the best of our knowledge, our results represent the most comprehensive results on near-optimal schedule shapes for deep neural network training, to date.

Scaling Collapse Reveals Universal Dynamics in Compute-Optimally Trained Neural Networks

What scaling limits govern neural network training dynamics when model size and training time grow in tandem? We show that despite the complex interactions between architecture, training algorithms, and data, compute-optimally trained models exhibit a remarkably precise universality. Specifically, loss curves from models of varying sizes collapse onto a single universal curve when training compute and loss are normalized to unity at the end of training. With learning rate decay, the collapse becomes so tight that differences in the normalized curves across models fall below the noise floor of individual loss curves across random seeds, a phenomenon we term supercollapse. We observe supercollapse across learning rate schedules, datasets, and architectures, including transformers trained on next-token prediction, and find it breaks down when hyperparameters are scaled suboptimally, providing a precise and practical indicator of good scaling. We explain these phenomena by connecting collapse to the power-law structure in typical neural scaling laws, and analyzing a simple yet surprisingly effective model of SGD noise dynamics that accurately predicts loss curves across various learning rate schedules and quantitatively explains the origin of supercollapse.

How far away are truly hyperparameter-free learning algorithms?

Despite major advances in methodology, hyperparameter tuning remains a crucial (and expensive) part of the development of machine learning systems. Even ignoring architectural choices, deep neural networks have a large number of optimization and regularization hyperparameters that need to be tuned carefully per workload in order to obtain the best results. In a perfect world, training algorithms would not require workload-specific hyperparameter tuning, but would instead have default settings that performed well across many workloads. Recently, there has been a growing literature on optimization methods which attempt to reduce the number of hyperparameters -- particularly the learning rate and its accompanying schedule. Given these developments, how far away is the dream of neural network training algorithms that completely obviate the need for painful tuning? In this paper, we evaluate the potential of learning-rate-free methods as components of hyperparameter-free methods. We freeze their (non-learning rate) hyperparameters to default values, and score their performance using the recently-proposed AlgoPerf: Training Algorithms benchmark. We found that literature-supplied default settings performed poorly on the benchmark, so we performed a search for hyperparameter configurations that performed well across all workloads simultaneously. The best AlgoPerf-calibrated learning-rate-free methods had much improved performance but still lagged slightly behind a similarly calibrated NadamW baseline in overall benchmark score. Our results suggest that there is still much room for improvement for learning-rate-free methods, and that testing against a strong, workload-agnostic baseline is important to improve hyperparameter reduction techniques.

Avoiding spurious sharpness minimization broadens applicability of SAM

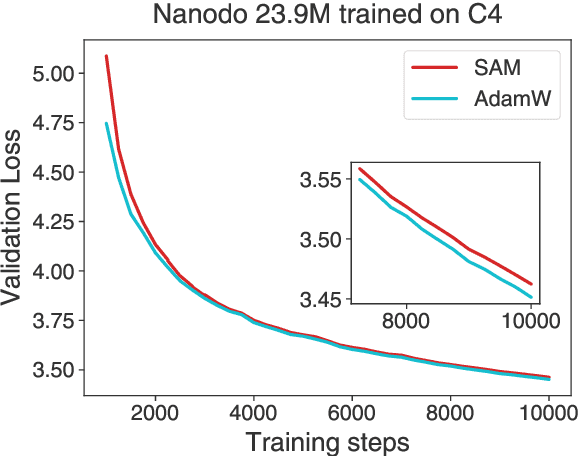
Curvature regularization techniques like Sharpness Aware Minimization (SAM) have shown great promise in improving generalization on vision tasks. However, we find that SAM performs poorly in domains like natural language processing (NLP), often degrading performance -- even with twice the compute budget. We investigate the discrepancy across domains and find that in the NLP setting, SAM is dominated by regularization of the logit statistics -- instead of improving the geometry of the function itself. We use this observation to develop an alternative algorithm we call Functional-SAM, which regularizes curvature only through modification of the statistics of the overall function implemented by the neural network, and avoids spurious minimization through logit manipulation. Furthermore, we argue that preconditioning the SAM perturbation also prevents spurious minimization, and when combined with Functional-SAM, it gives further improvements. Our proposed algorithms show improved performance over AdamW and SAM baselines when trained for an equal number of steps, in both fixed-length and Chinchilla-style training settings, at various model scales (including billion-parameter scale). On the whole, our work highlights the importance of more precise characterizations of sharpness in broadening the applicability of curvature regularization to large language models (LLMs).

Exact Risk Curves of signSGD in High-Dimensions: Quantifying Preconditioning and Noise-Compression Effects

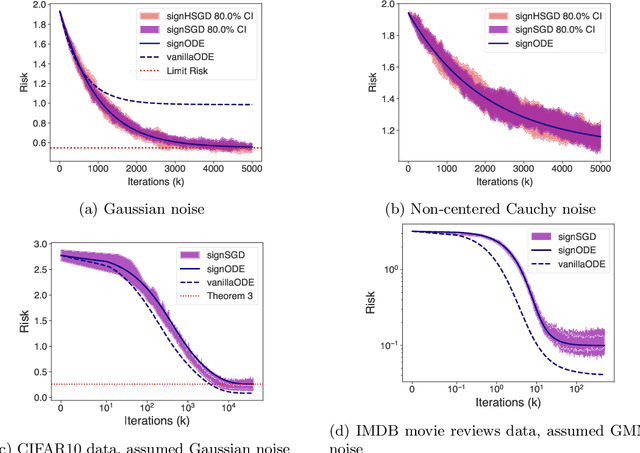
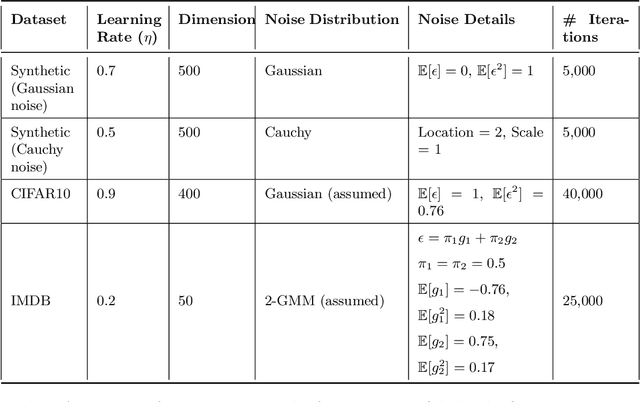
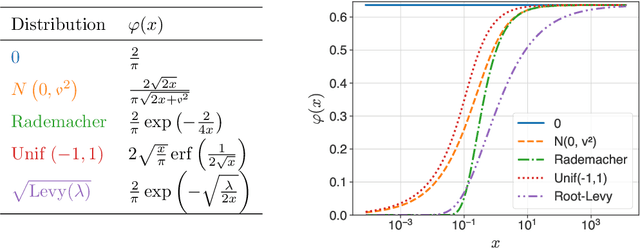
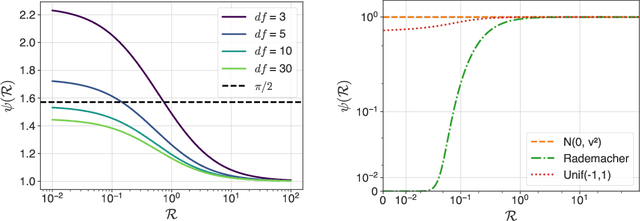
In recent years, signSGD has garnered interest as both a practical optimizer as well as a simple model to understand adaptive optimizers like Adam. Though there is a general consensus that signSGD acts to precondition optimization and reshapes noise, quantitatively understanding these effects in theoretically solvable settings remains difficult. We present an analysis of signSGD in a high dimensional limit, and derive a limiting SDE and ODE to describe the risk. Using this framework we quantify four effects of signSGD: effective learning rate, noise compression, diagonal preconditioning, and gradient noise reshaping. Our analysis is consistent with experimental observations but moves beyond that by quantifying the dependence of these effects on the data and noise distributions. We conclude with a conjecture on how these results might be extended to Adam.

Stepping on the Edge: Curvature Aware Learning Rate Tuners

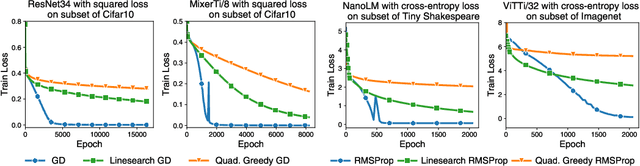
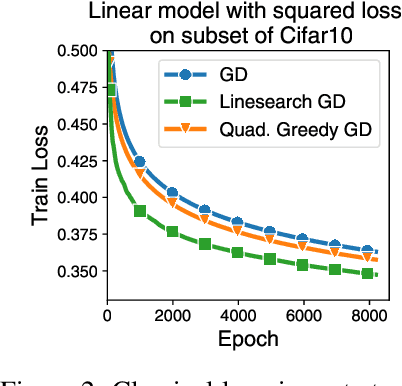
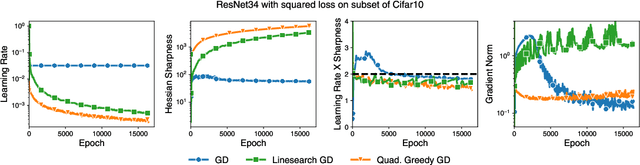
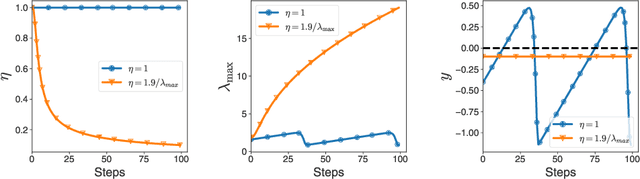
Curvature information -- particularly, the largest eigenvalue of the loss Hessian, known as the sharpness -- often forms the basis for learning rate tuners. However, recent work has shown that the curvature information undergoes complex dynamics during training, going from a phase of increasing sharpness to eventual stabilization. We analyze the closed-loop feedback effect between learning rate tuning and curvature. We find that classical learning rate tuners may yield greater one-step loss reduction, yet they ultimately underperform in the long term when compared to constant learning rates in the full batch regime. These models break the stabilization of the sharpness, which we explain using a simplified model of the joint dynamics of the learning rate and the curvature. To further investigate these effects, we introduce a new learning rate tuning method, Curvature Dynamics Aware Tuning (CDAT), which prioritizes long term curvature stabilization over instantaneous progress on the objective. In the full batch regime, CDAT shows behavior akin to prefixed warm-up schedules on deep learning objectives, outperforming tuned constant learning rates. In the mini batch regime, we observe that stochasticity introduces confounding effects that explain the previous success of some learning rate tuners at appropriate batch sizes. Our findings highlight the critical role of understanding the joint dynamics of the learning rate and curvature, beyond greedy minimization, to diagnose failures and design effective adaptive learning rate tuners.

A Clipped Trip: the Dynamics of SGD with Gradient Clipping in High-Dimensions

The success of modern machine learning is due in part to the adaptive optimization methods that have been developed to deal with the difficulties of training large models over complex datasets. One such method is gradient clipping: a practical procedure with limited theoretical underpinnings. In this work, we study clipping in a least squares problem under streaming SGD. We develop a theoretical analysis of the learning dynamics in the limit of large intrinsic dimension-a model and dataset dependent notion of dimensionality. In this limit we find a deterministic equation that describes the evolution of the loss. We show that with Gaussian noise clipping cannot improve SGD performance. Yet, in other noisy settings, clipping can provide benefits with tuning of the clipping threshold. In these cases, clipping biases updates in a way beneficial to training which cannot be recovered by SGD under any schedule. We conclude with a discussion about the links between high-dimensional clipping and neural network training.

High dimensional analysis reveals conservative sharpening and a stochastic edge of stability

Recent empirical and theoretical work has shown that the dynamics of the large eigenvalues of the training loss Hessian have some remarkably robust features across models and datasets in the full batch regime. There is often an early period of progressive sharpening where the large eigenvalues increase, followed by stabilization at a predictable value known as the edge of stability. Previous work showed that in the stochastic setting, the eigenvalues increase more slowly - a phenomenon we call conservative sharpening. We provide a theoretical analysis of a simple high-dimensional model which shows the origin of this slowdown. We also show that there is an alternative stochastic edge of stability which arises at small batch size that is sensitive to the trace of the Neural Tangent Kernel rather than the large Hessian eigenvalues. We conduct an experimental study which highlights the qualitative differences from the full batch phenomenology, and suggests that controlling the stochastic edge of stability can help optimization.

Gradient descent induces alignment between weights and the empirical NTK for deep non-linear networks

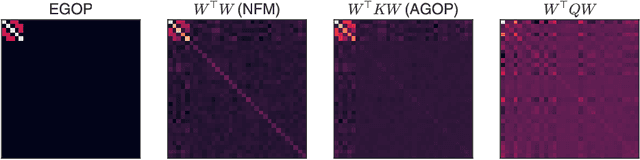
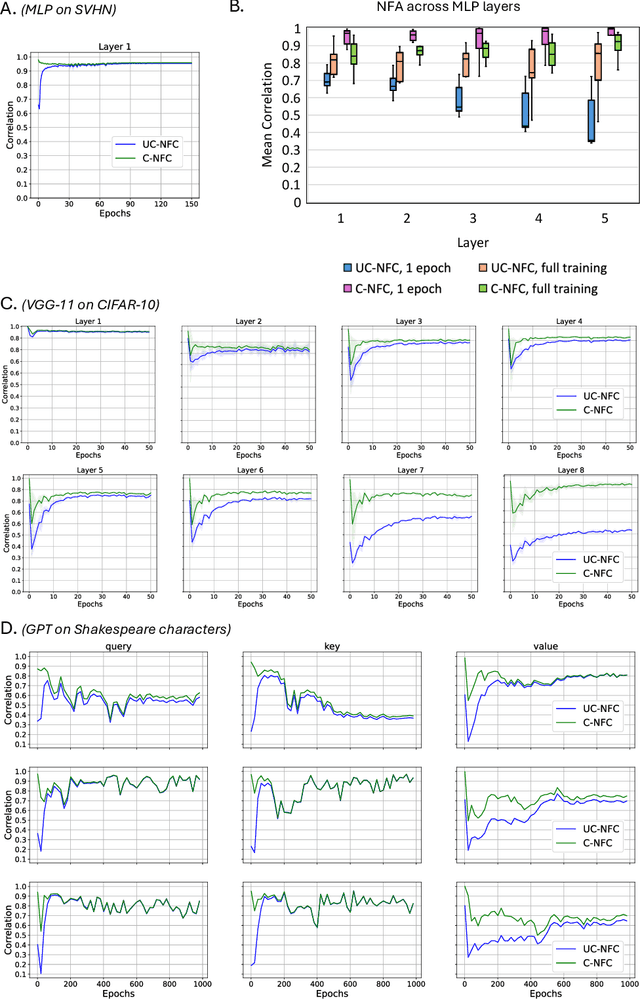
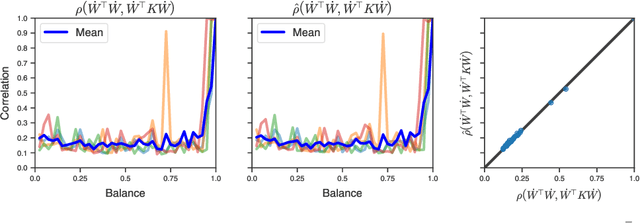
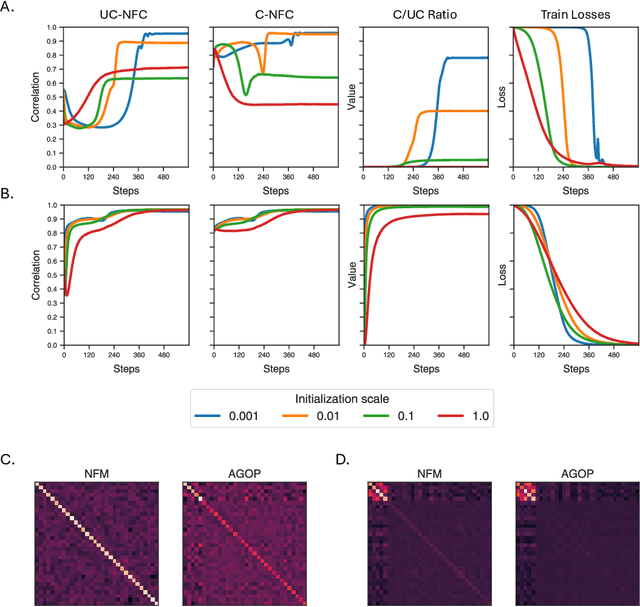
Understanding the mechanisms through which neural networks extract statistics from input-label pairs is one of the most important unsolved problems in supervised learning. Prior works have identified that the gram matrices of the weights in trained neural networks of general architectures are proportional to the average gradient outer product of the model, in a statement known as the Neural Feature Ansatz (NFA). However, the reason these quantities become correlated during training is poorly understood. In this work, we explain the emergence of this correlation. We identify that the NFA is equivalent to alignment between the left singular structure of the weight matrices and a significant component of the empirical neural tangent kernels associated with those weights. We establish that the NFA introduced in prior works is driven by a centered NFA that isolates this alignment. We show that the speed of NFA development can be predicted analytically at early training times in terms of simple statistics of the inputs and labels. Finally, we introduce a simple intervention to increase NFA correlation at any given layer, which dramatically improves the quality of features learned.

Neglected Hessian component explains mysteries in Sharpness regularization

Recent work has shown that methods like SAM which either explicitly or implicitly penalize second order information can improve generalization in deep learning. Seemingly similar methods like weight noise and gradient penalties often fail to provide such benefits. We show that these differences can be explained by the structure of the Hessian of the loss. First, we show that a common decomposition of the Hessian can be quantitatively interpreted as separating the feature exploitation from feature exploration. The feature exploration, which can be described by the Nonlinear Modeling Error matrix (NME), is commonly neglected in the literature since it vanishes at interpolation. Our work shows that the NME is in fact important as it can explain why gradient penalties are sensitive to the choice of activation function. Using this insight we design interventions to improve performance. We also provide evidence that challenges the long held equivalence of weight noise and gradient penalties. This equivalence relies on the assumption that the NME can be ignored, which we find does not hold for modern networks since they involve significant feature learning. We find that regularizing feature exploitation but not feature exploration yields performance similar to gradient penalties.