Gradient descent induces alignment between weights and the empirical NTK for deep non-linear networks
Paper and Code
Feb 07, 2024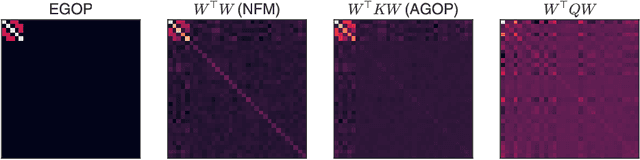
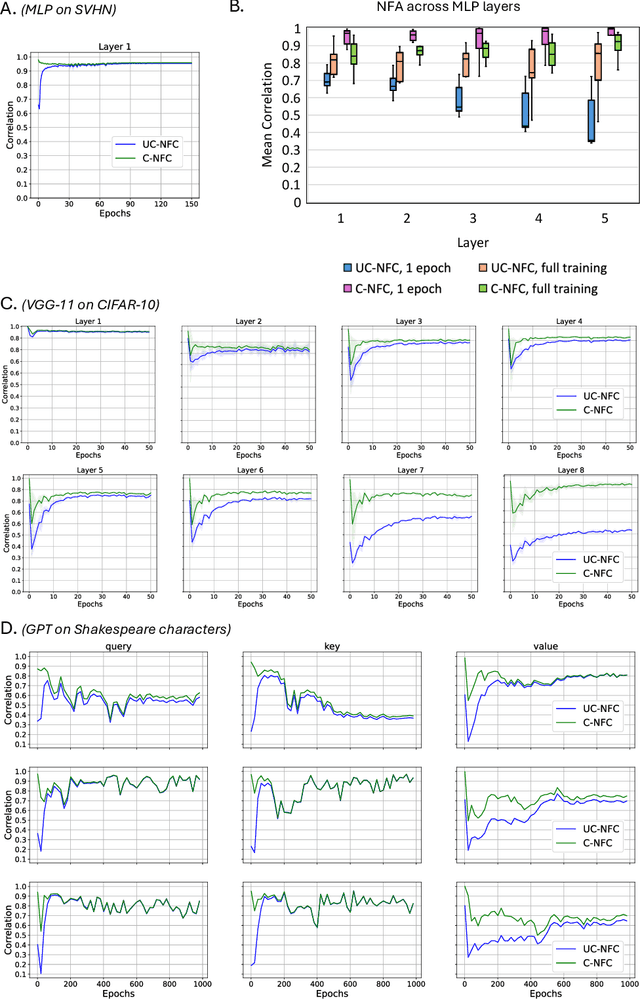
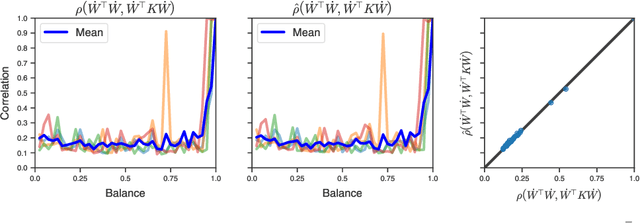
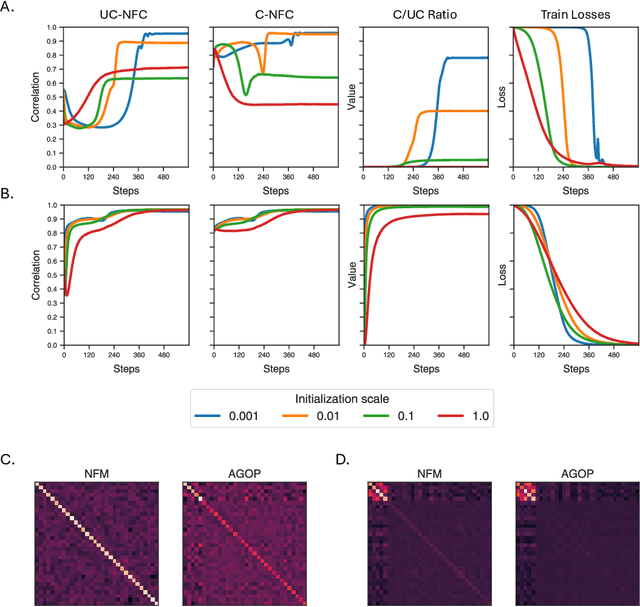
Understanding the mechanisms through which neural networks extract statistics from input-label pairs is one of the most important unsolved problems in supervised learning. Prior works have identified that the gram matrices of the weights in trained neural networks of general architectures are proportional to the average gradient outer product of the model, in a statement known as the Neural Feature Ansatz (NFA). However, the reason these quantities become correlated during training is poorly understood. In this work, we explain the emergence of this correlation. We identify that the NFA is equivalent to alignment between the left singular structure of the weight matrices and a significant component of the empirical neural tangent kernels associated with those weights. We establish that the NFA introduced in prior works is driven by a centered NFA that isolates this alignment. We show that the speed of NFA development can be predicted analytically at early training times in terms of simple statistics of the inputs and labels. Finally, we introduce a simple intervention to increase NFA correlation at any given layer, which dramatically improves the quality of features learned.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge