Mathieu Blondel
DMA, CNRS
Learning with Local Search MCMC Layers
May 20, 2025Abstract:Integrating combinatorial optimization layers into neural networks has recently attracted significant research interest. However, many existing approaches lack theoretical guarantees or fail to perform adequately when relying on inexact solvers. This is a critical limitation, as many operations research problems are NP-hard, often necessitating the use of neighborhood-based local search heuristics. These heuristics iteratively generate and evaluate candidate solutions based on an acceptance rule. In this paper, we introduce a theoretically-principled approach for learning with such inexact combinatorial solvers. Inspired by the connection between simulated annealing and Metropolis-Hastings, we propose to transform problem-specific neighborhood systems used in local search heuristics into proposal distributions, implementing MCMC on the combinatorial space of feasible solutions. This allows us to construct differentiable combinatorial layers and associated loss functions. Replacing an exact solver by a local search strongly reduces the computational burden of learning on many applications. We demonstrate our approach on a large-scale dynamic vehicle routing problem with time windows.
On Teacher Hacking in Language Model Distillation
Feb 04, 2025



Abstract:Post-training of language models (LMs) increasingly relies on the following two stages: (i) knowledge distillation, where the LM is trained to imitate a larger teacher LM, and (ii) reinforcement learning from human feedback (RLHF), where the LM is aligned by optimizing a reward model. In the second RLHF stage, a well-known challenge is reward hacking, where the LM over-optimizes the reward model. Such phenomenon is in line with Goodhart's law and can lead to degraded performance on the true objective. In this paper, we investigate whether a similar phenomenon, that we call teacher hacking, can occur during knowledge distillation. This could arise because the teacher LM is itself an imperfect approximation of the true distribution. To study this, we propose a controlled experimental setup involving: (i) an oracle LM representing the ground-truth distribution, (ii) a teacher LM distilled from the oracle, and (iii) a student LM distilled from the teacher. Our experiments reveal the following insights. When using a fixed offline dataset for distillation, teacher hacking occurs; moreover, we can detect it by observing when the optimization process deviates from polynomial convergence laws. In contrast, employing online data generation techniques effectively mitigates teacher hacking. More precisely, we identify data diversity as the key factor in preventing hacking. Overall, our findings provide a deeper understanding of the benefits and limitations of distillation for building robust and efficient LMs.
Joint Learning of Energy-based Models and their Partition Function
Jan 30, 2025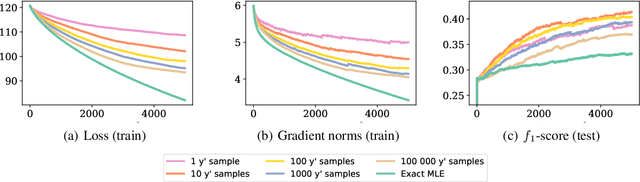
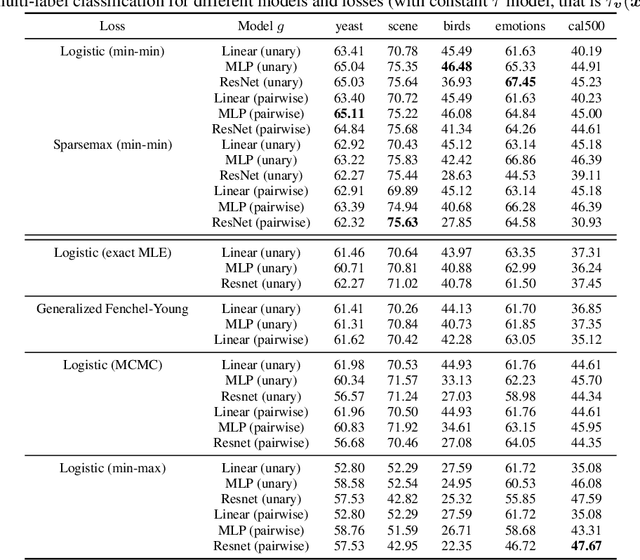
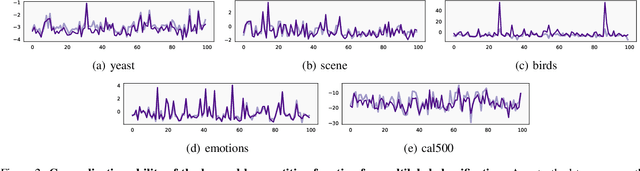
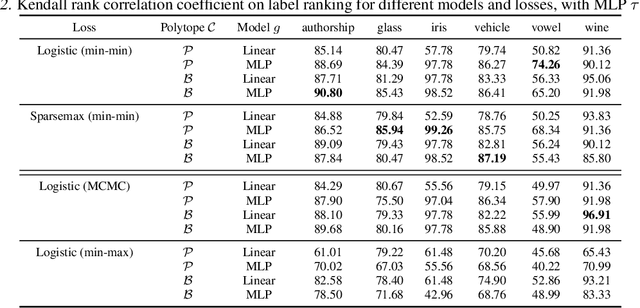
Abstract:Energy-based models (EBMs) offer a flexible framework for parameterizing probability distributions using neural networks. However, learning EBMs by exact maximum likelihood estimation (MLE) is generally intractable, due to the need to compute the partition function (normalization constant). In this paper, we propose a novel formulation for approximately learning probabilistic EBMs in combinatorially-large discrete spaces, such as sets or permutations. Our key idea is to jointly learn both an energy model and its log-partition, both parameterized as a neural network. Our approach not only provides a novel tractable objective criterion to learn EBMs by stochastic gradient descent (without relying on MCMC), but also a novel means to estimate the log-partition function on unseen data points. On the theoretical side, we show that our approach recovers the optimal MLE solution when optimizing in the space of continuous functions. Furthermore, we show that our approach naturally extends to the broader family of Fenchel-Young losses, allowing us to obtain the first tractable method for optimizing the sparsemax loss in combinatorially-large spaces. We demonstrate our approach on multilabel classification and label ranking.
Loss Functions and Operators Generated by f-Divergences
Jan 30, 2025Abstract:The logistic loss (a.k.a. cross-entropy loss) is one of the most popular loss functions used for multiclass classification. It is also the loss function of choice for next-token prediction in language modeling. It is associated with the Kullback--Leibler (KL) divergence and the softargmax operator. In this work, we propose to construct new convex loss functions based on $f$-divergences. Our loss functions generalize the logistic loss in two directions: i) by replacing the KL divergence with $f$-divergences and ii) by allowing non-uniform reference measures. We instantiate our framework for numerous $f$-divergences, recovering existing losses and creating new ones. By analogy with the logistic loss, the loss function generated by an $f$-divergence is associated with an operator, that we dub $f$-softargmax. We derive a novel parallelizable bisection algorithm for computing the $f$-softargmax associated with any $f$-divergence. On the empirical side, one of the goals of this paper is to determine the effectiveness of loss functions beyond the classical cross-entropy in a language model setting, including on pre-training, post-training (SFT) and distillation. We show that the loss function generated by the $\alpha$-divergence (which is equivalent to Tsallis $\alpha$-negentropy in the case of unit reference measures) with $\alpha=1.5$ performs well across several tasks.
Stepping on the Edge: Curvature Aware Learning Rate Tuners
Jul 08, 2024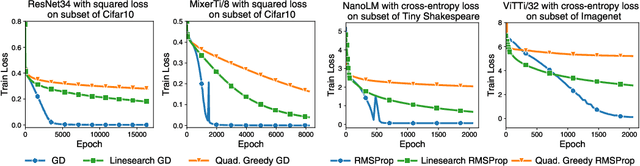
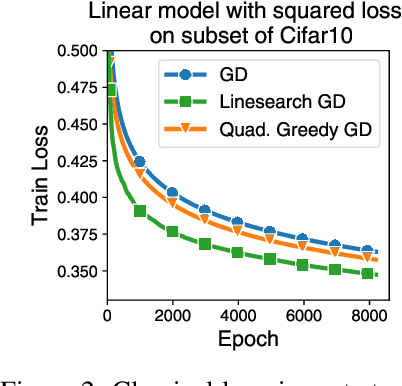
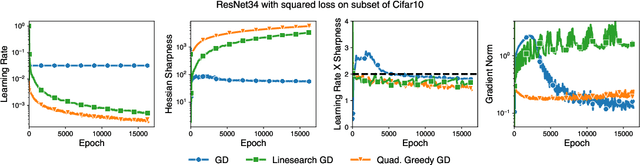
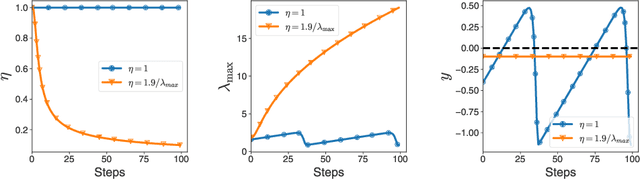
Abstract:Curvature information -- particularly, the largest eigenvalue of the loss Hessian, known as the sharpness -- often forms the basis for learning rate tuners. However, recent work has shown that the curvature information undergoes complex dynamics during training, going from a phase of increasing sharpness to eventual stabilization. We analyze the closed-loop feedback effect between learning rate tuning and curvature. We find that classical learning rate tuners may yield greater one-step loss reduction, yet they ultimately underperform in the long term when compared to constant learning rates in the full batch regime. These models break the stabilization of the sharpness, which we explain using a simplified model of the joint dynamics of the learning rate and the curvature. To further investigate these effects, we introduce a new learning rate tuning method, Curvature Dynamics Aware Tuning (CDAT), which prioritizes long term curvature stabilization over instantaneous progress on the objective. In the full batch regime, CDAT shows behavior akin to prefixed warm-up schedules on deep learning objectives, outperforming tuned constant learning rates. In the mini batch regime, we observe that stochasticity introduces confounding effects that explain the previous success of some learning rate tuners at appropriate batch sizes. Our findings highlight the critical role of understanding the joint dynamics of the learning rate and curvature, beyond greedy minimization, to diagnose failures and design effective adaptive learning rate tuners.
Learning with Fitzpatrick Losses
May 23, 2024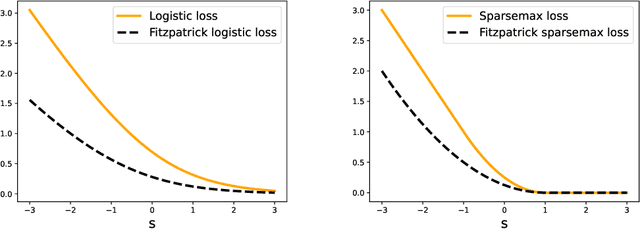
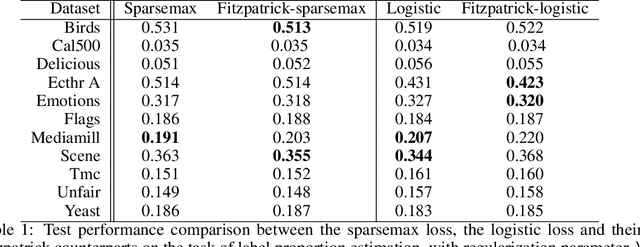
Abstract:Fenchel-Young losses are a family of convex loss functions, encompassing the squared, logistic and sparsemax losses, among others. Each Fenchel-Young loss is implicitly associated with a link function, for mapping model outputs to predictions. For instance, the logistic loss is associated with the soft argmax link function. Can we build new loss functions associated with the same link function as Fenchel-Young losses? In this paper, we introduce Fitzpatrick losses, a new family of convex loss functions based on the Fitzpatrick function. A well-known theoretical tool in maximal monotone operator theory, the Fitzpatrick function naturally leads to a refined Fenchel-Young inequality, making Fitzpatrick losses tighter than Fenchel-Young losses, while maintaining the same link function for prediction. As an example, we introduce the Fitzpatrick logistic loss and the Fitzpatrick sparsemax loss, counterparts of the logistic and the sparsemax losses. This yields two new tighter losses associated with the soft argmax and the sparse argmax, two of the most ubiquitous output layers used in machine learning. We study in details the properties of Fitzpatrick losses and in particular, we show that they can be seen as Fenchel-Young losses using a modified, target-dependent generating function. We demonstrate the effectiveness of Fitzpatrick losses for label proportion estimation.
The Elements of Differentiable Programming
Mar 21, 2024
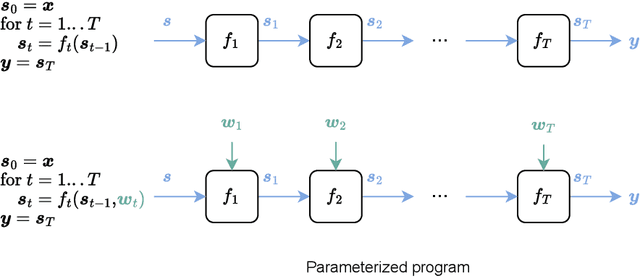

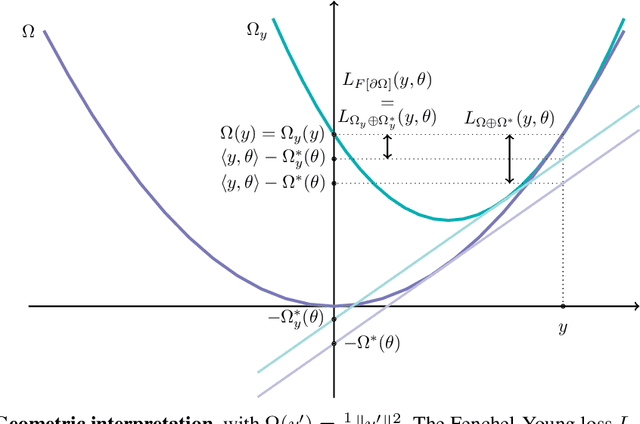
Abstract:Artificial intelligence has recently experienced remarkable advances, fueled by large models, vast datasets, accelerated hardware, and, last but not least, the transformative power of differentiable programming. This new programming paradigm enables end-to-end differentiation of complex computer programs (including those with control flows and data structures), making gradient-based optimization of program parameters possible. As an emerging paradigm, differentiable programming builds upon several areas of computer science and applied mathematics, including automatic differentiation, graphical models, optimization and statistics. This book presents a comprehensive review of the fundamental concepts useful for differentiable programming. We adopt two main perspectives, that of optimization and that of probability, with clear analogies between the two. Differentiable programming is not merely the differentiation of programs, but also the thoughtful design of programs intended for differentiation. By making programs differentiable, we inherently introduce probability distributions over their execution, providing a means to quantify the uncertainty associated with program outputs.
Implicit Diffusion: Efficient Optimization through Stochastic Sampling
Feb 08, 2024



Abstract:We present a new algorithm to optimize distributions defined implicitly by parameterized stochastic diffusions. Doing so allows us to modify the outcome distribution of sampling processes by optimizing over their parameters. We introduce a general framework for first-order optimization of these processes, that performs jointly, in a single loop, optimization and sampling steps. This approach is inspired by recent advances in bilevel optimization and automatic implicit differentiation, leveraging the point of view of sampling as optimization over the space of probability distributions. We provide theoretical guarantees on the performance of our method, as well as experimental results demonstrating its effectiveness in real-world settings.
How do Transformers perform In-Context Autoregressive Learning?
Feb 08, 2024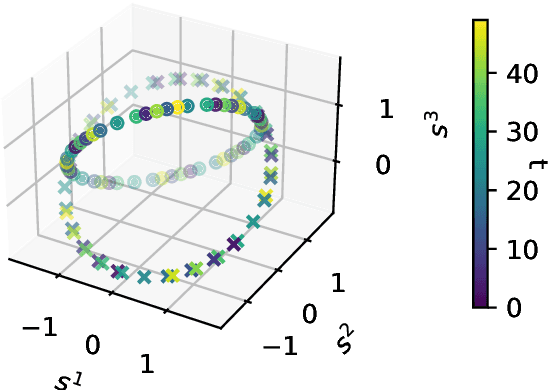
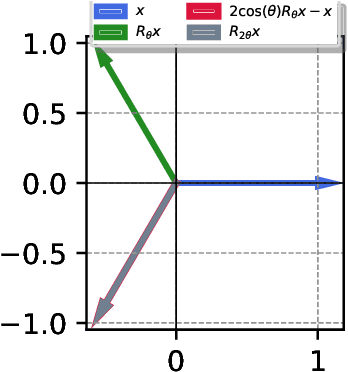

Abstract:Transformers have achieved state-of-the-art performance in language modeling tasks. However, the reasons behind their tremendous success are still unclear. In this paper, towards a better understanding, we train a Transformer model on a simple next token prediction task, where sequences are generated as a first-order autoregressive process $s_{t+1} = W s_t$. We show how a trained Transformer predicts the next token by first learning $W$ in-context, then applying a prediction mapping. We call the resulting procedure in-context autoregressive learning. More precisely, focusing on commuting orthogonal matrices $W$, we first show that a trained one-layer linear Transformer implements one step of gradient descent for the minimization of an inner objective function, when considering augmented tokens. When the tokens are not augmented, we characterize the global minima of a one-layer diagonal linear multi-head Transformer. Importantly, we exhibit orthogonality between heads and show that positional encoding captures trigonometric relations in the data. On the experimental side, we consider the general case of non-commuting orthogonal matrices and generalize our theoretical findings.
Direct Language Model Alignment from Online AI Feedback
Feb 07, 2024



Abstract:Direct alignment from preferences (DAP) methods, such as DPO, have recently emerged as efficient alternatives to reinforcement learning from human feedback (RLHF), that do not require a separate reward model. However, the preference datasets used in DAP methods are usually collected ahead of training and never updated, thus the feedback is purely offline. Moreover, responses in these datasets are often sampled from a language model distinct from the one being aligned, and since the model evolves over training, the alignment phase is inevitably off-policy. In this study, we posit that online feedback is key and improves DAP methods. Our method, online AI feedback (OAIF), uses an LLM as annotator: on each training iteration, we sample two responses from the current model and prompt the LLM annotator to choose which one is preferred, thus providing online feedback. Despite its simplicity, we demonstrate via human evaluation in several tasks that OAIF outperforms both offline DAP and RLHF methods. We further show that the feedback leveraged in OAIF is easily controllable, via instruction prompts to the LLM annotator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge