Fast Best-of-N Decoding via Speculative Rejection

The safe and effective deployment of Large Language Models (LLMs) involves a critical step called alignment, which ensures that the model's responses are in accordance with human preferences. Prevalent alignment techniques, such as DPO, PPO and their variants, align LLMs by changing the pre-trained model weights during a phase called post-training. While predominant, these post-training methods add substantial complexity before LLMs can be deployed. Inference-time alignment methods avoid the complex post-training step and instead bias the generation towards responses that are aligned with human preferences. The best-known inference-time alignment method, called Best-of-N, is as effective as the state-of-the-art post-training procedures. Unfortunately, Best-of-N requires vastly more resources at inference time than standard decoding strategies, which makes it computationally not viable. In this work, we introduce Speculative Rejection, a computationally-viable inference-time alignment algorithm. It generates high-scoring responses according to a given reward model, like Best-of-N does, while being between 16 to 32 times more computationally efficient.

FutureFill: Fast Generation from Convolutional Sequence Models

We address the challenge of efficient auto-regressive generation in sequence prediction models by introducing FutureFill: a method for fast generation that applies to any sequence prediction algorithm based on convolutional operators. Our approach reduces the generation time requirement from linear to square root relative to the context length. Additionally, FutureFill requires a prefill cache sized only by the number of tokens generated, which is smaller than the cache requirements for standard convolutional and attention-based models. We validate our theoretical findings with experimental evidence demonstrating correctness and efficiency gains in a synthetic generation task.

Implicit Diffusion: Efficient Optimization through Stochastic Sampling

We present a new algorithm to optimize distributions defined implicitly by parameterized stochastic diffusions. Doing so allows us to modify the outcome distribution of sampling processes by optimizing over their parameters. We introduce a general framework for first-order optimization of these processes, that performs jointly, in a single loop, optimization and sampling steps. This approach is inspired by recent advances in bilevel optimization and automatic implicit differentiation, leveraging the point of view of sampling as optimization over the space of probability distributions. We provide theoretical guarantees on the performance of our method, as well as experimental results demonstrating its effectiveness in real-world settings.

Contextual Bandits with Stage-wise Constraints

We study contextual bandits in the presence of a stage-wise constraint (a constraint at each round), when the constraint must be satisfied both with high probability and in expectation. Obviously the setting where the constraint is in expectation is a relaxation of the one with high probability. We start with the linear case where both the contextual bandit problem (reward function) and the stage-wise constraint (cost function) are linear. In each of the high probability and in expectation settings, we propose an upper-confidence bound algorithm for the problem and prove a $T$-round regret bound for it. Our algorithms balance exploration and constraint satisfaction using a novel idea that scales the radii of the reward and cost confidence sets with different scaling factors. We also prove a lower-bound for this constrained problem, show how our algorithms and analyses can be extended to multiple constraints, and provide simulations to validate our theoretical results. In the high probability setting, we describe the minimum requirements for the action set in order for our algorithm to be tractable. In the setting that the constraint is in expectation, we further specialize our results to multi-armed bandits and propose a computationally efficient algorithm for this setting with regret analysis. Finally, we extend our results to the case where the reward and cost functions are both non-linear. We propose an algorithm for this case and prove a regret bound for it that characterize the function class complexity by the eluder dimension.

Can a Transformer Represent a Kalman Filter?

Transformers are a class of autoregressive deep learning architectures which have recently achieved state-of-the-art performance in various vision, language, and robotics tasks. We revisit the problem of Kalman Filtering in linear dynamical systems and show that Transformers can approximate the Kalman Filter in a strong sense. Specifically, for any observable LTI system we construct an explicit causally-masked Transformer which implements the Kalman Filter, up to a small additive error which is bounded uniformly in time; we call our construction the Transformer Filter. Our construction is based on a two-step reduction. We first show that a softmax self-attention block can exactly represent a certain Gaussian kernel smoothing estimator. We then show that this estimator closely approximates the Kalman Filter. We also investigate how the Transformer Filter can be used for measurement-feedback control and prove that the resulting nonlinear controllers closely approximate the performance of standard optimal control policies such as the LQG controller.

Joint Representation Training in Sequential Tasks with Shared Structure

Classical theory in reinforcement learning (RL) predominantly focuses on the single task setting, where an agent learns to solve a task through trial-and-error experience, given access to data only from that task. However, many recent empirical works have demonstrated the significant practical benefits of leveraging a joint representation trained across multiple, related tasks. In this work we theoretically analyze such a setting, formalizing the concept of task relatedness as a shared state-action representation that admits linear dynamics in all the tasks. We introduce the Shared-MatrixRL algorithm for the setting of Multitask MatrixRL. In the presence of $P$ episodic tasks of dimension $d$ sharing a joint $r \ll d$ low-dimensional representation, we show the regret on the the $P$ tasks can be improved from $O(PHd\sqrt{NH})$ to $O((Hd\sqrt{rP} + HP\sqrt{rd})\sqrt{NH})$ over $N$ episodes of horizon $H$. These gains coincide with those observed in other linear models in contextual bandits and RL. In contrast with previous work that have studied multi task RL in other function approximation models, we show that in the presence of bilinear optimization oracle and finite state action spaces there exists a computationally efficient algorithm for multitask MatrixRL via a reduction to quadratic programming. We also develop a simple technique to shave off a $\sqrt{H}$ factor from the regret upper bounds of some episodic linear problems.

Generalization Bounds for Data-Driven Numerical Linear Algebra

Data-driven algorithms can adapt their internal structure or parameters to inputs from unknown application-specific distributions, by learning from a training sample of inputs. Several recent works have applied this approach to problems in numerical linear algebra, obtaining significant empirical gains in performance. However, no theoretical explanation for their success was known. In this work we prove generalization bounds for those algorithms, within the PAC-learning framework for data-driven algorithm selection proposed by Gupta and Roughgarden (SICOMP 2017). Our main results are closely matching upper and lower bounds on the fat shattering dimension of the learning-based low rank approximation algorithm of Indyk et al.~(NeurIPS 2019). Our techniques are general, and provide generalization bounds for many other recently proposed data-driven algorithms in numerical linear algebra, covering both sketching-based and multigrid-based methods. This considerably broadens the class of data-driven algorithms for which a PAC-learning analysis is available.

A Sharp Characterization of Linear Estimators for Offline Policy Evaluation

Offline policy evaluation is a fundamental statistical problem in reinforcement learning that involves estimating the value function of some decision-making policy given data collected by a potentially different policy. In order to tackle problems with complex, high-dimensional observations, there has been significant interest from theoreticians and practitioners alike in understanding the possibility of function approximation in reinforcement learning. Despite significant study, a sharp characterization of when we might expect offline policy evaluation to be tractable, even in the simplest setting of linear function approximation, has so far remained elusive, with a surprising number of strong negative results recently appearing in the literature. In this work, we identify simple control-theoretic and linear-algebraic conditions that are necessary and sufficient for classical methods, in particular Fitted Q-iteration (FQI) and least squares temporal difference learning (LSTD), to succeed at offline policy evaluation. Using this characterization, we establish a precise hierarchy of regimes under which these estimators succeed. We prove that LSTD works under strictly weaker conditions than FQI. Furthermore, we establish that if a problem is not solvable via LSTD, then it cannot be solved by a broad class of linear estimators, even in the limit of infinite data. Taken together, our results provide a complete picture of the behavior of linear estimators for offline policy evaluation (OPE), unify previously disparate analyses of canonical algorithms, and provide significantly sharper notions of the underlying statistical complexity of OPE.

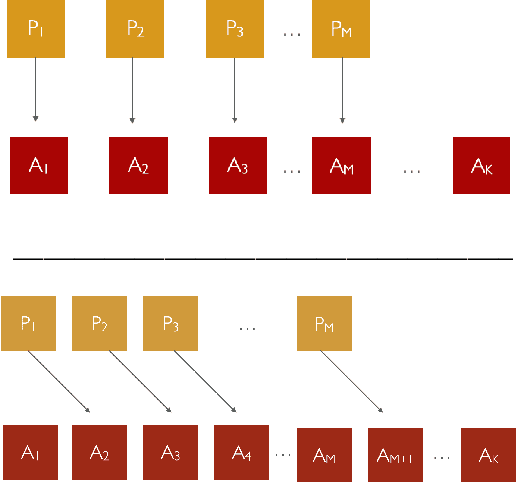
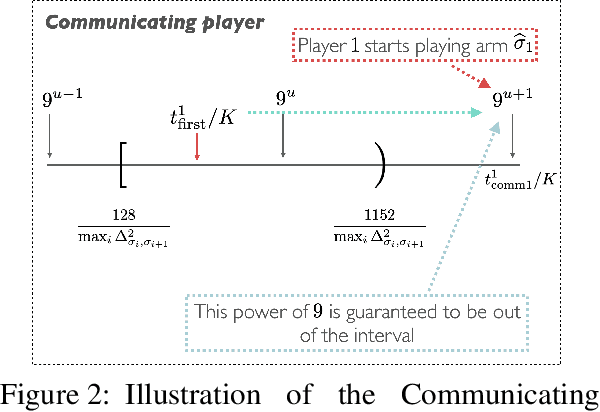
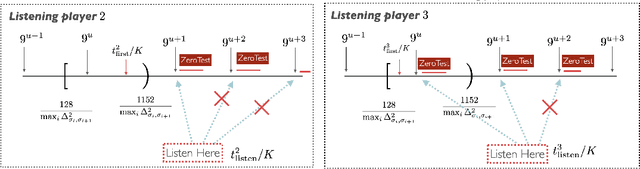
An Instance-Dependent Analysis for the Cooperative Multi-Player Multi-Armed Bandit

We study the problem of information sharing and cooperation in Multi-Player Multi-Armed bandits. We propose the first algorithm that achieves logarithmic regret for this problem. Our results are based on two innovations. First, we show that a simple modification to a successive elimination strategy can be used to allow the players to estimate their suboptimality gaps, up to constant factors, in the absence of collisions. Second, we leverage the first result to design a communication protocol that successfully uses the small reward of collisions to coordinate among players, while preserving meaningful instance-dependent logarithmic regret guarantees.

Parallelizing Contextual Linear Bandits

Standard approaches to decision-making under uncertainty focus on sequential exploration of the space of decisions. However, \textit{simultaneously} proposing a batch of decisions, which leverages available resources for parallel experimentation, has the potential to rapidly accelerate exploration. We present a family of (parallel) contextual linear bandit algorithms, whose regret is nearly identical to their perfectly sequential counterparts -- given access to the same total number of oracle queries -- up to a lower-order "burn-in" term that is dependent on the context-set geometry. We provide matching information-theoretic lower bounds on parallel regret performance to establish our algorithms are asymptotically optimal in the time horizon. Finally, we also present an empirical evaluation of these parallel algorithms in several domains, including materials discovery and biological sequence design problems, to demonstrate the utility of parallelized bandits in practical settings.