Benefits of Early Stopping in Gradient Descent for Overparameterized Logistic Regression

In overparameterized logistic regression, gradient descent (GD) iterates diverge in norm while converging in direction to the maximum $\ell_2$-margin solution -- a phenomenon known as the implicit bias of GD. This work investigates additional regularization effects induced by early stopping in well-specified high-dimensional logistic regression. We first demonstrate that the excess logistic risk vanishes for early-stopped GD but diverges to infinity for GD iterates at convergence. This suggests that early-stopped GD is well-calibrated, whereas asymptotic GD is statistically inconsistent. Second, we show that to attain a small excess zero-one risk, polynomially many samples are sufficient for early-stopped GD, while exponentially many samples are necessary for any interpolating estimator, including asymptotic GD. This separation underscores the statistical benefits of early stopping in the overparameterized regime. Finally, we establish nonasymptotic bounds on the norm and angular differences between early-stopped GD and $\ell_2$-regularized empirical risk minimizer, thereby connecting the implicit regularization of GD with explicit $\ell_2$-regularization.

One-layer transformers fail to solve the induction heads task

A simple communication complexity argument proves that no one-layer transformer can solve the induction heads task unless its size is exponentially larger than the size sufficient for a two-layer transformer.

Spectrum Extraction and Clipping for Implicitly Linear Layers

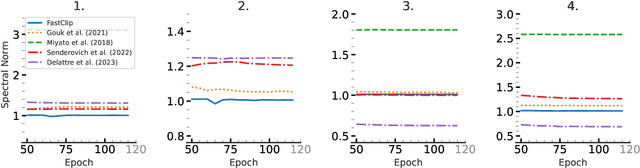
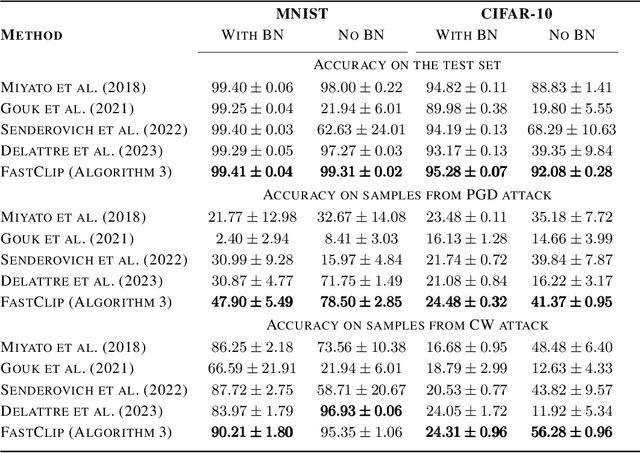
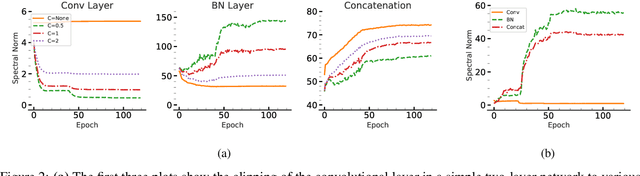
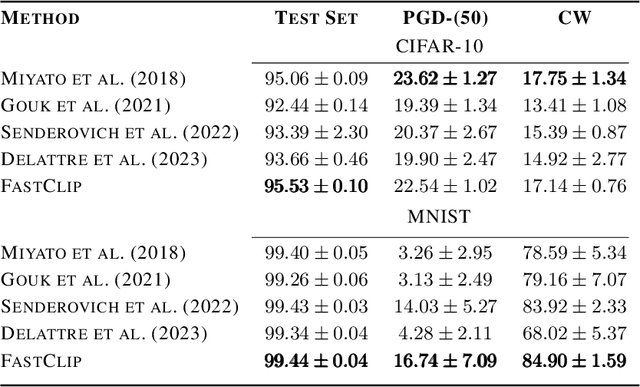
We show the effectiveness of automatic differentiation in efficiently and correctly computing and controlling the spectrum of implicitly linear operators, a rich family of layer types including all standard convolutional and dense layers. We provide the first clipping method which is correct for general convolution layers, and illuminate the representational limitation that caused correctness issues in prior work. We study the effect of the batch normalization layers when concatenated with convolutional layers and show how our clipping method can be applied to their composition. By comparing the accuracy and performance of our algorithms to the state-of-the-art methods, using various experiments, we show they are more precise and efficient and lead to better generalization and adversarial robustness. We provide the code for using our methods at https://github.com/Ali-E/FastClip.

Large Stepsize Gradient Descent for Logistic Loss: Non-Monotonicity of the Loss Improves Optimization Efficiency

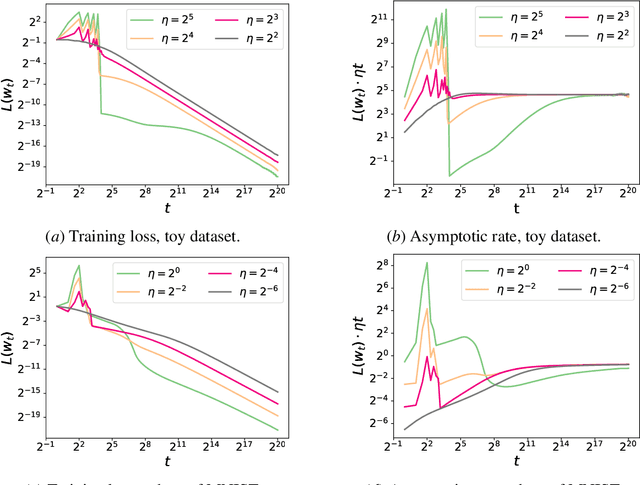
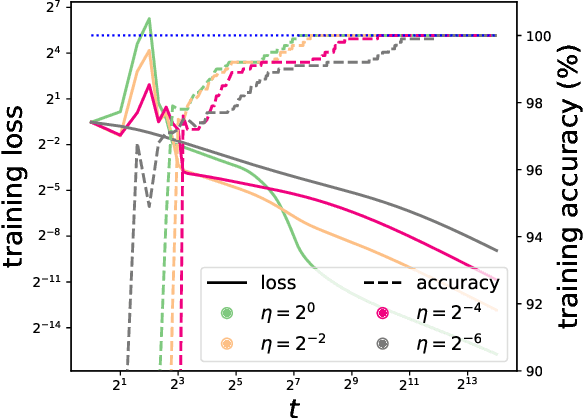
We consider gradient descent (GD) with a constant stepsize applied to logistic regression with linearly separable data, where the constant stepsize $\eta$ is so large that the loss initially oscillates. We show that GD exits this initial oscillatory phase rapidly -- in $\mathcal{O}(\eta)$ steps -- and subsequently achieves an $\tilde{\mathcal{O}}(1 / (\eta t) )$ convergence rate after $t$ additional steps. Our results imply that, given a budget of $T$ steps, GD can achieve an accelerated loss of $\tilde{\mathcal{O}}(1/T^2)$ with an aggressive stepsize $\eta:= \Theta( T)$, without any use of momentum or variable stepsize schedulers. Our proof technique is versatile and also handles general classification loss functions (where exponential tails are needed for the $\tilde{\mathcal{O}}(1/T^2)$ acceleration), nonlinear predictors in the neural tangent kernel regime, and online stochastic gradient descent (SGD) with a large stepsize, under suitable separability conditions.

Transformers, parallel computation, and logarithmic depth

We show that a constant number of self-attention layers can efficiently simulate, and be simulated by, a constant number of communication rounds of Massively Parallel Computation. As a consequence, we show that logarithmic depth is sufficient for transformers to solve basic computational tasks that cannot be efficiently solved by several other neural sequence models and sub-quadratic transformer approximations. We thus establish parallelism as a key distinguishing property of transformers.

On Achieving Optimal Adversarial Test Error

We first elucidate various fundamental properties of optimal adversarial predictors: the structure of optimal adversarial convex predictors in terms of optimal adversarial zero-one predictors, bounds relating the adversarial convex loss to the adversarial zero-one loss, and the fact that continuous predictors can get arbitrarily close to the optimal adversarial error for both convex and zero-one losses. Applying these results along with new Rademacher complexity bounds for adversarial training near initialization, we prove that for general data distributions and perturbation sets, adversarial training on shallow networks with early stopping and an idealized optimal adversary is able to achieve optimal adversarial test error. By contrast, prior theoretical work either considered specialized data distributions or only provided training error guarantees.

Representational Strengths and Limitations of Transformers

Attention layers, as commonly used in transformers, form the backbone of modern deep learning, yet there is no mathematical description of their benefits and deficiencies as compared with other architectures. In this work we establish both positive and negative results on the representation power of attention layers, with a focus on intrinsic complexity parameters such as width, depth, and embedding dimension. On the positive side, we present a sparse averaging task, where recurrent networks and feedforward networks all have complexity scaling polynomially in the input size, whereas transformers scale merely logarithmically in the input size; furthermore, we use the same construction to show the necessity and role of a large embedding dimension in a transformer. On the negative side, we present a triple detection task, where attention layers in turn have complexity scaling linearly in the input size; as this scenario seems rare in practice, we also present natural variants that can be efficiently solved by attention layers. The proof techniques emphasize the value of communication complexity in the analysis of transformers and related models, and the role of sparse averaging as a prototypical attention task, which even finds use in the analysis of triple detection.

Feature selection with gradient descent on two-layer networks in low-rotation regimes

This work establishes low test error of gradient flow (GF) and stochastic gradient descent (SGD) on two-layer ReLU networks with standard initialization, in three regimes where key sets of weights rotate little (either naturally due to GF and SGD, or due to an artificial constraint), and making use of margins as the core analytic technique. The first regime is near initialization, specifically until the weights have moved by $\mathcal{O}(\sqrt m)$, where $m$ denotes the network width, which is in sharp contrast to the $\mathcal{O}(1)$ weight motion allowed by the Neural Tangent Kernel (NTK); here it is shown that GF and SGD only need a network width and number of samples inversely proportional to the NTK margin, and moreover that GF attains at least the NTK margin itself, which suffices to establish escape from bad KKT points of the margin objective, whereas prior work could only establish nondecreasing but arbitrarily small margins. The second regime is the Neural Collapse (NC) setting, where data lies in extremely-well-separated groups, and the sample complexity scales with the number of groups; here the contribution over prior work is an analysis of the entire GF trajectory from initialization. Lastly, if the inner layer weights are constrained to change in norm only and can not rotate, then GF with large widths achieves globally maximal margins, and its sample complexity scales with their inverse; this is in contrast to prior work, which required infinite width and a tricky dual convergence assumption. As purely technical contributions, this work develops a variety of potential functions and other tools which will hopefully aid future work.

Convex Analysis at Infinity: An Introduction to Astral Space

Not all convex functions on $\mathbb{R}^n$ have finite minimizers; some can only be minimized by a sequence as it heads to infinity. In this work, we aim to develop a theory for understanding such minimizers at infinity. We study astral space, a compact extension of $\mathbb{R}^n$ to which such points at infinity have been added. Astral space is constructed to be as small as possible while still ensuring that all linear functions can be continuously extended to the new space. Although astral space includes all of $\mathbb{R}^n$, it is not a vector space, nor even a metric space. However, it is sufficiently well-structured to allow useful and meaningful extensions of concepts of convexity, conjugacy, and subdifferentials. We develop these concepts and analyze various properties of convex functions on astral space, including the detailed structure of their minimizers, exact characterizations of continuity, and convergence of descent algorithms.

Stochastic linear optimization never overfits with quadratically-bounded losses on general data

This work shows that a diverse collection of linear optimization methods, when run on general data, fail to overfit, despite lacking any explicit constraints or regularization: with high probability, their trajectories stay near the curve of optimal constrained solutions over the population distribution. This analysis is powered by an elementary but flexible proof scheme which can handle many settings, summarized as follows. Firstly, the data can be general: unlike other implicit bias works, it need not satisfy large margin or other structural conditions, and moreover can arrive sequentially IID, sequentially following a Markov chain, as a batch, and lastly it can have heavy tails. Secondly, while the main analysis is for mirror descent, rates are also provided for the Temporal-Difference fixed-point method from reinforcement learning; all prior high probability analyses in these settings required bounded iterates, bounded updates, bounded noise, or some equivalent. Thirdly, the losses are general, and for instance the logistic and squared losses can be handled simultaneously, unlike other implicit bias works. In all of these settings, not only is low population error guaranteed with high probability, but moreover low sample complexity is guaranteed so long as there exists any low-complexity near-optimal solution, even if the global problem structure and in particular global optima have high complexity.