Stochastic linear optimization never overfits with quadratically-bounded losses on general data
Paper and Code
Feb 14, 2022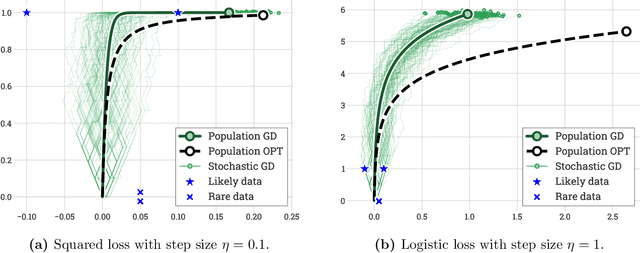
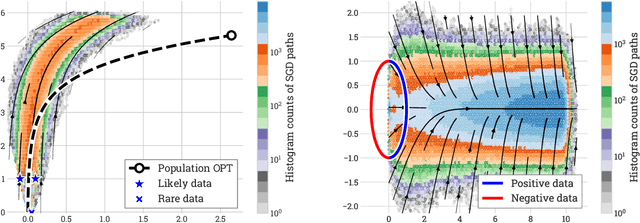
This work shows that a diverse collection of linear optimization methods, when run on general data, fail to overfit, despite lacking any explicit constraints or regularization: with high probability, their trajectories stay near the curve of optimal constrained solutions over the population distribution. This analysis is powered by an elementary but flexible proof scheme which can handle many settings, summarized as follows. Firstly, the data can be general: unlike other implicit bias works, it need not satisfy large margin or other structural conditions, and moreover can arrive sequentially IID, sequentially following a Markov chain, as a batch, and lastly it can have heavy tails. Secondly, while the main analysis is for mirror descent, rates are also provided for the Temporal-Difference fixed-point method from reinforcement learning; all prior high probability analyses in these settings required bounded iterates, bounded updates, bounded noise, or some equivalent. Thirdly, the losses are general, and for instance the logistic and squared losses can be handled simultaneously, unlike other implicit bias works. In all of these settings, not only is low population error guaranteed with high probability, but moreover low sample complexity is guaranteed so long as there exists any low-complexity near-optimal solution, even if the global problem structure and in particular global optima have high complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge