SureMap: Simultaneous Mean Estimation for Single-Task and Multi-Task Disaggregated Evaluation

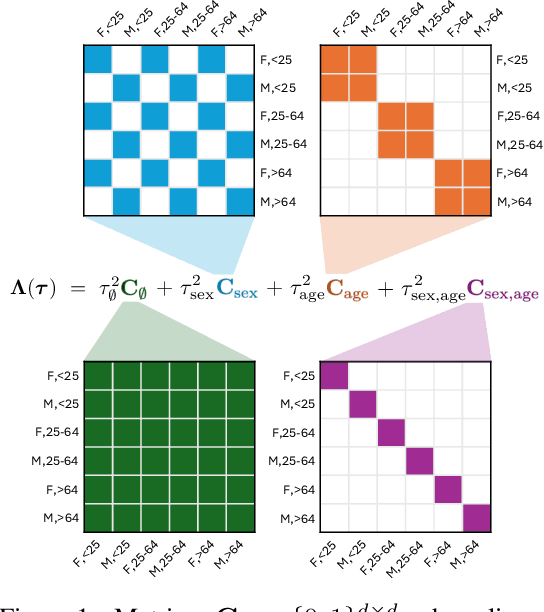
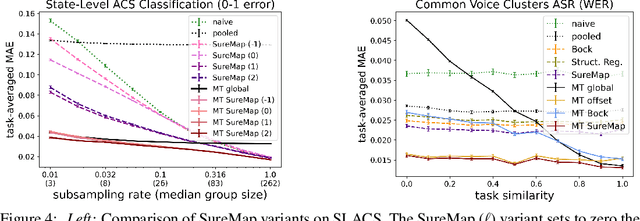
Disaggregated evaluation -- estimation of performance of a machine learning model on different subpopulations -- is a core task when assessing performance and group-fairness of AI systems. A key challenge is that evaluation data is scarce, and subpopulations arising from intersections of attributes (e.g., race, sex, age) are often tiny. Today, it is common for multiple clients to procure the same AI model from a model developer, and the task of disaggregated evaluation is faced by each customer individually. This gives rise to what we call the multi-task disaggregated evaluation problem, wherein multiple clients seek to conduct a disaggregated evaluation of a given model in their own data setting (task). In this work we develop a disaggregated evaluation method called SureMap that has high estimation accuracy for both multi-task and single-task disaggregated evaluations of blackbox models. SureMap's efficiency gains come from (1) transforming the problem into structured simultaneous Gaussian mean estimation and (2) incorporating external data, e.g., from the AI system creator or from their other clients. Our method combines maximum a posteriori (MAP) estimation using a well-chosen prior together with cross-validation-free tuning via Stein's unbiased risk estimate (SURE). We evaluate SureMap on disaggregated evaluation tasks in multiple domains, observing significant accuracy improvements over several strong competitors.

Fairlearn: Assessing and Improving Fairness of AI Systems

Fairlearn is an open source project to help practitioners assess and improve fairness of artificial intelligence (AI) systems. The associated Python library, also named fairlearn, supports evaluation of a model's output across affected populations and includes several algorithms for mitigating fairness issues. Grounded in the understanding that fairness is a sociotechnical challenge, the project integrates learning resources that aid practitioners in considering a system's broader societal context.

Convex Analysis at Infinity: An Introduction to Astral Space

Not all convex functions on $\mathbb{R}^n$ have finite minimizers; some can only be minimized by a sequence as it heads to infinity. In this work, we aim to develop a theory for understanding such minimizers at infinity. We study astral space, a compact extension of $\mathbb{R}^n$ to which such points at infinity have been added. Astral space is constructed to be as small as possible while still ensuring that all linear functions can be continuously extended to the new space. Although astral space includes all of $\mathbb{R}^n$, it is not a vector space, nor even a metric space. However, it is sufficiently well-structured to allow useful and meaningful extensions of concepts of convexity, conjugacy, and subdifferentials. We develop these concepts and analyze various properties of convex functions on astral space, including the detailed structure of their minimizers, exact characterizations of continuity, and convergence of descent algorithms.

Bayesian decision-making under misspecified priors with applications to meta-learning

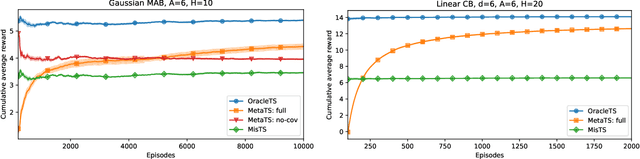
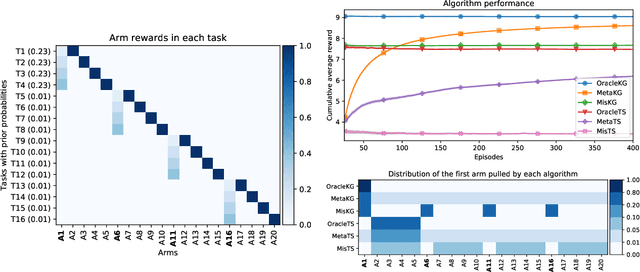
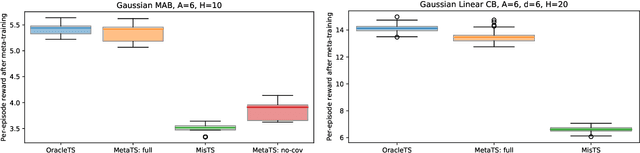
Thompson sampling and other Bayesian sequential decision-making algorithms are among the most popular approaches to tackle explore/exploit trade-offs in (contextual) bandits. The choice of prior in these algorithms offers flexibility to encode domain knowledge but can also lead to poor performance when misspecified. In this paper, we demonstrate that performance degrades gracefully with misspecification. We prove that the expected reward accrued by Thompson sampling (TS) with a misspecified prior differs by at most $\tilde{\mathcal{O}}(H^2 \epsilon)$ from TS with a well specified prior, where $\epsilon$ is the total-variation distance between priors and $H$ is the learning horizon. Our bound does not require the prior to have any parametric form. For priors with bounded support, our bound is independent of the cardinality or structure of the action space, and we show that it is tight up to universal constants in the worst case. Building on our sensitivity analysis, we establish generic PAC guarantees for algorithms in the recently studied Bayesian meta-learning setting and derive corollaries for various families of priors. Our results generalize along two axes: (1) they apply to a broader family of Bayesian decision-making algorithms, including a Monte-Carlo implementation of the knowledge gradient algorithm (KG), and (2) they apply to Bayesian POMDPs, the most general Bayesian decision-making setting, encompassing contextual bandits as a special case. Through numerical simulations, we illustrate how prior misspecification and the deployment of one-step look-ahead (as in KG) can impact the convergence of meta-learning in multi-armed and contextual bandits with structured and correlated priors.

Gradient descent follows the regularization path for general losses

Recent work across many machine learning disciplines has highlighted that standard descent methods, even without explicit regularization, do not merely minimize the training error, but also exhibit an implicit bias. This bias is typically towards a certain regularized solution, and relies upon the details of the learning process, for instance the use of the cross-entropy loss. In this work, we show that for empirical risk minimization over linear predictors with arbitrary convex, strictly decreasing losses, if the risk does not attain its infimum, then the gradient-descent path and the algorithm-independent regularization path converge to the same direction (whenever either converges to a direction). Using this result, we provide a justification for the widely-used exponentially-tailed losses (such as the exponential loss or the logistic loss): while this convergence to a direction for exponentially-tailed losses is necessarily to the maximum-margin direction, other losses such as polynomially-tailed losses may induce convergence to a direction with a poor margin.

Doubly robust off-policy evaluation with shrinkage

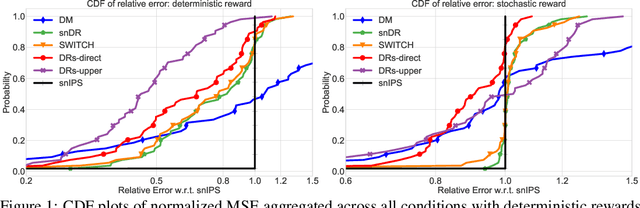
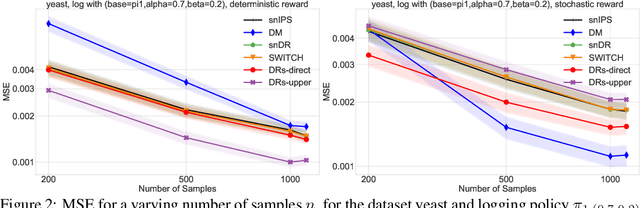
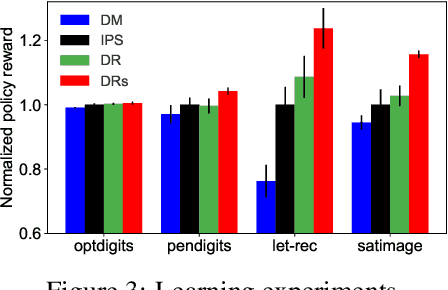
We design a new family of estimators for off-policy evaluation in contextual bandits. Our estimators are based on the asymptotically optimal approach of doubly robust estimation, but they shrink importance weights to obtain a better bias-variance tradeoff in finite samples. Our approach adapts importance weights to the quality of a reward predictor, interpolating between doubly robust estimation and direct modeling. When the reward predictor is poor, we recover previously studied weight clipping, but when the reward predictor is good, we obtain a new form of shrinkage. To navigate between these regimes and tune the shrinkage coefficient, we design a model selection procedure, which we prove is never worse than the doubly robust estimator. Extensive experiments on bandit benchmark problems show that our estimators are highly adaptive and typically outperform state-of-the-art methods.

Fair Regression: Quantitative Definitions and Reduction-based Algorithms

In this paper, we study the prediction of a real-valued target, such as a risk score or recidivism rate, while guaranteeing a quantitative notion of fairness with respect to a protected attribute such as gender or race. We call this class of problems \emph{fair regression}. We propose general schemes for fair regression under two notions of fairness: (1) statistical parity, which asks that the prediction be statistically independent of the protected attribute, and (2) bounded group loss, which asks that the prediction error restricted to any protected group remain below some pre-determined level. While we only study these two notions of fairness, our schemes are applicable to arbitrary Lipschitz-continuous losses, and so they encompass least-squares regression, logistic regression, quantile regression, and many other tasks. Our schemes only require access to standard risk minimization algorithms (such as standard classification or least-squares regression) while providing theoretical guarantees on the optimality and fairness of the obtained solutions. In addition to analyzing theoretical properties of our schemes, we empirically demonstrate their ability to uncover fairness--accuracy frontiers on several standard datasets.

Provably efficient RL with Rich Observations via Latent State Decoding

We study the exploration problem in episodic MDPs with rich observations generated from a small number of latent states. Under certain identifiability assumptions, we demonstrate how to estimate a mapping from the observations to latent states inductively through a sequence of regression and clustering steps---where previously decoded latent states provide labels for later regression problems---and use it to construct good exploration policies. We provide finite-sample guarantees on the quality of the learned state decoding function and exploration policies, and complement our theory with an empirical evaluation on a class of hard exploration problems. Our method exponentially improves over $Q$-learning with na\"ive exploration, even when $Q$-learning has cheating access to latent states.

A Reductions Approach to Fair Classification

We present a systematic approach for achieving fairness in a binary classification setting. While we focus on two well-known quantitative definitions of fairness, our approach encompasses many other previously studied definitions as special cases. The key idea is to reduce fair classification to a sequence of cost-sensitive classification problems, whose solutions yield a randomized classifier with the lowest (empirical) error subject to the desired constraints. We introduce two reductions that work for any representation of the cost-sensitive classifier and compare favorably to prior baselines on a variety of data sets, while overcoming several of their disadvantages.

Hierarchical Imitation and Reinforcement Learning

We study how to effectively leverage expert feedback to learn sequential decision-making policies. We focus on problems with sparse rewards and long time horizons, which typically pose significant challenges in reinforcement learning. We propose an algorithmic framework, called hierarchical guidance, that leverages the hierarchical structure of the underlying problem to integrate different modes of expert interaction. Our framework can incorporate different combinations of imitation learning (IL) and reinforcement learning (RL) at different levels, leading to dramatic reductions in both expert effort and cost of exploration. Using long-horizon benchmarks, including Montezuma's Revenge, we demonstrate that our approach can learn significantly faster than hierarchical RL, and be significantly more label-efficient than standard IL. We also theoretically analyze labeling cost for certain instantiations of our framework.