Contextual Dynamic Pricing with Heterogeneous Buyers

We initiate the study of contextual dynamic pricing with a heterogeneous population of buyers, where a seller repeatedly posts prices (over $T$ rounds) that depend on the observable $d$-dimensional context and receives binary purchase feedback. Unlike prior work assuming homogeneous buyer types, in our setting the buyer's valuation type is drawn from an unknown distribution with finite support size $K_{\star}$. We develop a contextual pricing algorithm based on optimistic posterior sampling with regret $\widetilde{O}(K_{\star}\sqrt{dT})$, which we prove to be tight in $d$ and $T$ up to logarithmic terms. Finally, we refine our analysis for the non-contextual pricing case, proposing a variance-aware zooming algorithm that achieves the optimal dependence on $K_{\star}$.

Scheduling with Uncertain Holding Costs and its Application to Content Moderation

In content moderation for social media platforms, the cost of delaying the review of a content is proportional to its view trajectory, which fluctuates and is apriori unknown. Motivated by such uncertain holding costs, we consider a queueing model where job states evolve based on a Markov chain with state-dependent instantaneous holding costs. We demonstrate that in the presence of such uncertain holding costs, the two canonical algorithmic principles, instantaneous-cost ($c\mu$-rule) and expected-remaining-cost ($c\mu/\theta$-rule), are suboptimal. By viewing each job as a Markovian ski-rental problem, we develop a new index-based algorithm, Opportunity-adjusted Remaining Cost (OaRC), that adjusts to the opportunity of serving jobs in the future when uncertainty partly resolves. We show that the regret of OaRC scales as $\tilde{O}(L^{1.5}\sqrt{N})$, where $L$ is the maximum length of a job's holding cost trajectory and $N$ is the system size. This regret bound shows that OaRC achieves asymptotic optimality when the system size $N$ scales to infinity. Moreover, its regret is independent of the state-space size, which is a desirable property when job states contain contextual information. We corroborate our results with an extensive simulation study based on two holding cost patterns (online ads and user-generated content) that arise in content moderation for social media platforms. Our simulations based on synthetic and real datasets demonstrate that OaRC consistently outperforms existing practice, which is based on the two canonical algorithmic principles.

Learning to Defer in Content Moderation: The Human-AI Interplay

Successful content moderation in online platforms relies on a human-AI collaboration approach. A typical heuristic estimates the expected harmfulness of a post and uses fixed thresholds to decide whether to remove it and whether to send it for human review. This disregards the prediction uncertainty, the time-varying element of human review capacity and post arrivals, and the selective sampling in the dataset (humans only review posts filtered by the admission algorithm). In this paper, we introduce a model to capture the human-AI interplay in content moderation. The algorithm observes contextual information for incoming posts, makes classification and admission decisions, and schedules posts for human review. Only admitted posts receive human reviews on their harmfulness. These reviews help educate the machine-learning algorithms but are delayed due to congestion in the human review system. The classical learning-theoretic way to capture this human-AI interplay is via the framework of learning to defer, where the algorithm has the option to defer a classification task to humans for a fixed cost and immediately receive feedback. Our model contributes to this literature by introducing congestion in the human review system. Moreover, unlike work on online learning with delayed feedback where the delay in the feedback is exogenous to the algorithm's decisions, the delay in our model is endogenous to both the admission and the scheduling decisions. We propose a near-optimal learning algorithm that carefully balances the classification loss from a selectively sampled dataset, the idiosyncratic loss of non-reviewed posts, and the delay loss of having congestion in the human review system. To the best of our knowledge, this is the first result for online learning in contextual queueing systems and hence our analytical framework may be of independent interest.

Quantifying the Cost of Learning in Queueing Systems

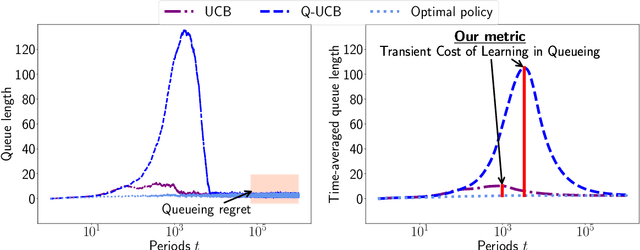
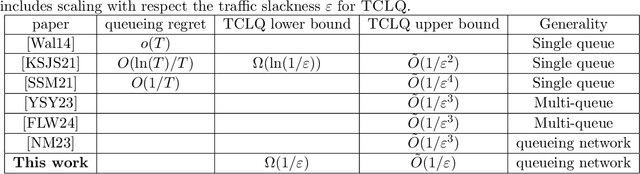
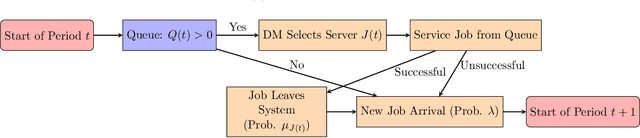
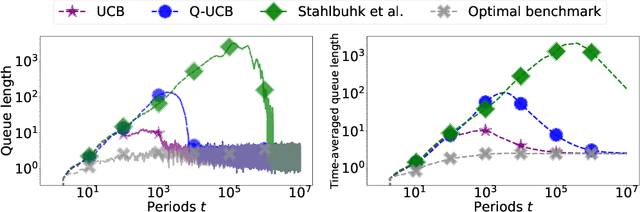
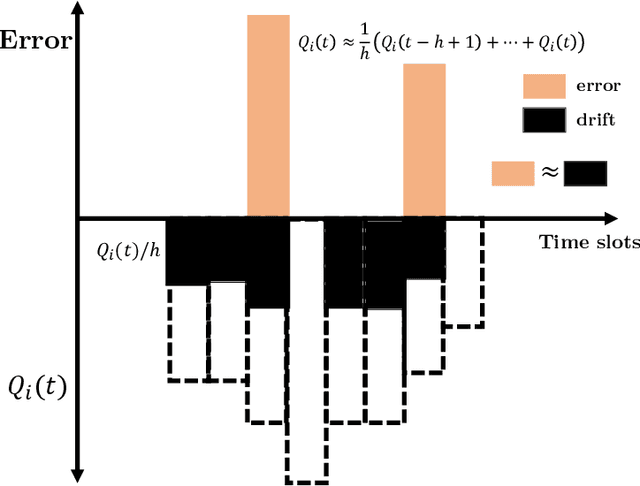
Queueing systems are widely applicable stochastic models with use cases in communication networks, healthcare, service systems, etc. Although their optimal control has been extensively studied, most existing approaches assume perfect knowledge of system parameters. Of course, this assumption rarely holds in practice where there is parameter uncertainty, thus motivating a recent line of work on bandit learning for queueing systems. This nascent stream of research focuses on the asymptotic performance of the proposed algorithms. In this paper, we argue that an asymptotic metric, which focuses on late-stage performance, is insufficient to capture the intrinsic statistical complexity of learning in queueing systems which typically occurs in the early stage. Instead, we propose the Cost of Learning in Queueing (CLQ), a new metric that quantifies the maximum increase in time-averaged queue length caused by parameter uncertainty. We characterize the CLQ of a single-queue multi-server system, and then extend these results to multi-queue multi-server systems and networks of queues. In establishing our results, we propose a unified analysis framework for CLQ that bridges Lyapunov and bandit analysis, which could be of independent interest.

Learning in Stackelberg Games with Non-myopic Agents

We study Stackelberg games where a principal repeatedly interacts with a long-lived, non-myopic agent, without knowing the agent's payoff function. Although learning in Stackelberg games is well-understood when the agent is myopic, non-myopic agents pose additional complications. In particular, non-myopic agents may strategically select actions that are inferior in the present to mislead the principal's learning algorithm and obtain better outcomes in the future. We provide a general framework that reduces learning in presence of non-myopic agents to robust bandit optimization in the presence of myopic agents. Through the design and analysis of minimally reactive bandit algorithms, our reduction trades off the statistical efficiency of the principal's learning algorithm against its effectiveness in inducing near-best-responses. We apply this framework to Stackelberg security games (SSGs), pricing with unknown demand curve, strategic classification, and general finite Stackelberg games. In each setting, we characterize the type and impact of misspecifications present in near-best-responses and develop a learning algorithm robust to such misspecifications. Along the way, we improve the query complexity of learning in SSGs with $n$ targets from the state-of-the-art $O(n^3)$ to a near-optimal $\widetilde{O}(n)$ by uncovering a fundamental structural property of such games. This result is of independent interest beyond learning with non-myopic agents.

Efficient decentralized multi-agent learning in asymmetric queuing systems

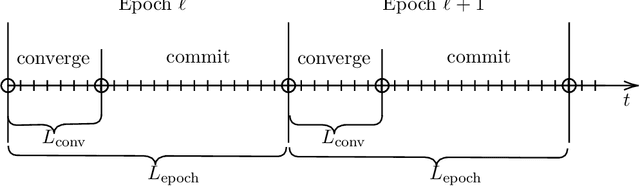
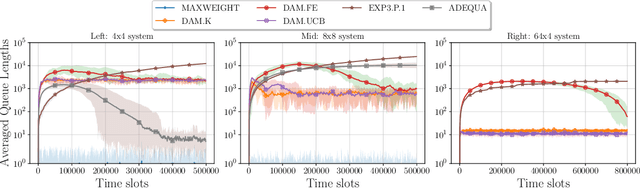
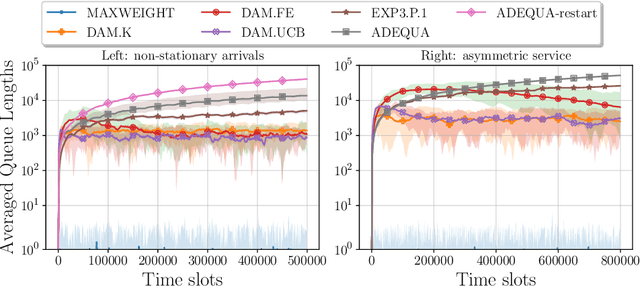
We study decentralized multi-agent learning in bipartite queuing systems, a standard model for service systems. In particular, $N$ agents request service from $K$ servers in a fully decentralized way, i.e, by running the same algorithm without communication. Previous decentralized algorithms are restricted to symmetric systems, have performance that is degrading exponentially in the number of servers, require communication through shared randomness and unique agent identities, and are computationally demanding. In contrast, we provide a simple learning algorithm that, when run decentrally by each agent, leads the queuing system to have efficient performance in general asymmetric bipartite queuing systems while also having additional robustness properties. Along the way, we provide the first UCB-based algorithm for the centralized case of the problem, which resolves an open question by Krishnasamy et al. (2016,2021).

Bayesian decision-making under misspecified priors with applications to meta-learning

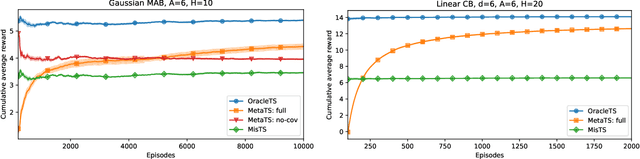
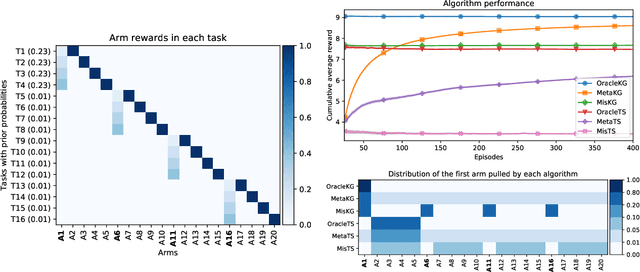
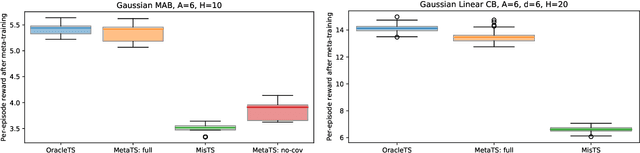
Thompson sampling and other Bayesian sequential decision-making algorithms are among the most popular approaches to tackle explore/exploit trade-offs in (contextual) bandits. The choice of prior in these algorithms offers flexibility to encode domain knowledge but can also lead to poor performance when misspecified. In this paper, we demonstrate that performance degrades gracefully with misspecification. We prove that the expected reward accrued by Thompson sampling (TS) with a misspecified prior differs by at most $\tilde{\mathcal{O}}(H^2 \epsilon)$ from TS with a well specified prior, where $\epsilon$ is the total-variation distance between priors and $H$ is the learning horizon. Our bound does not require the prior to have any parametric form. For priors with bounded support, our bound is independent of the cardinality or structure of the action space, and we show that it is tight up to universal constants in the worst case. Building on our sensitivity analysis, we establish generic PAC guarantees for algorithms in the recently studied Bayesian meta-learning setting and derive corollaries for various families of priors. Our results generalize along two axes: (1) they apply to a broader family of Bayesian decision-making algorithms, including a Monte-Carlo implementation of the knowledge gradient algorithm (KG), and (2) they apply to Bayesian POMDPs, the most general Bayesian decision-making setting, encompassing contextual bandits as a special case. Through numerical simulations, we illustrate how prior misspecification and the deployment of one-step look-ahead (as in KG) can impact the convergence of meta-learning in multi-armed and contextual bandits with structured and correlated priors.

Constrained episodic reinforcement learning in concave-convex and knapsack settings

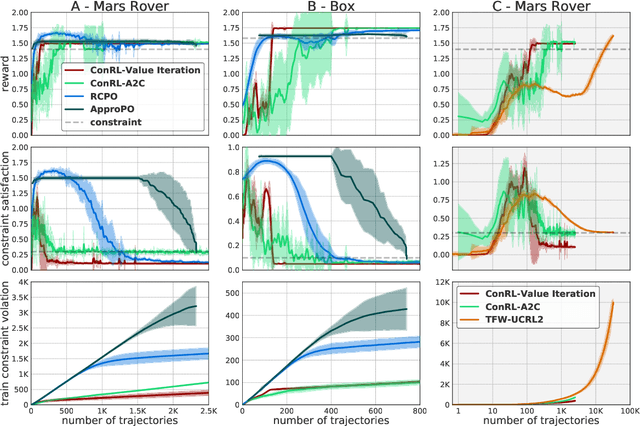
We propose an algorithm for tabular episodic reinforcement learning with constraints. We provide a modular analysis with strong theoretical guarantees for settings with concave rewards and convex constraints, and for settings with hard constraints (knapsacks). Most of the previous work in constrained reinforcement learning is limited to linear constraints, and the remaining work focuses on either the feasibility question or settings with a single episode. Our experiments demonstrate that the proposed algorithm significantly outperforms these approaches in existing constrained episodic environments.

Bandits with adversarial scaling

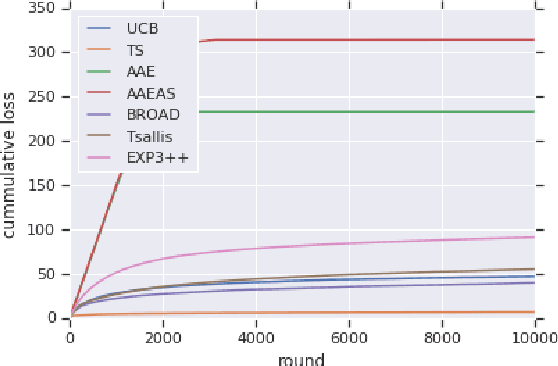
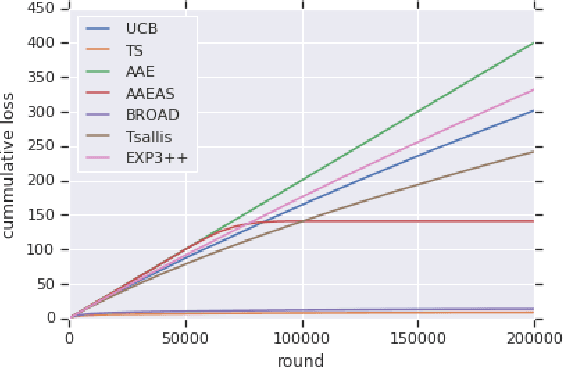
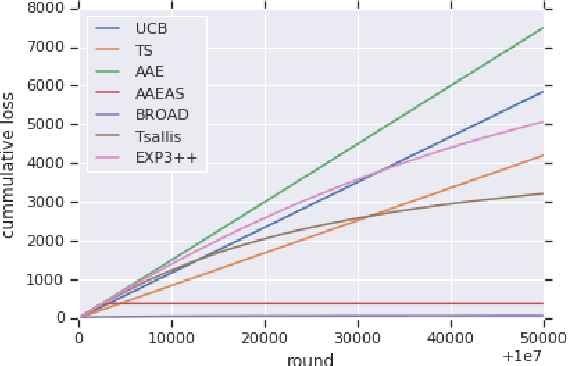
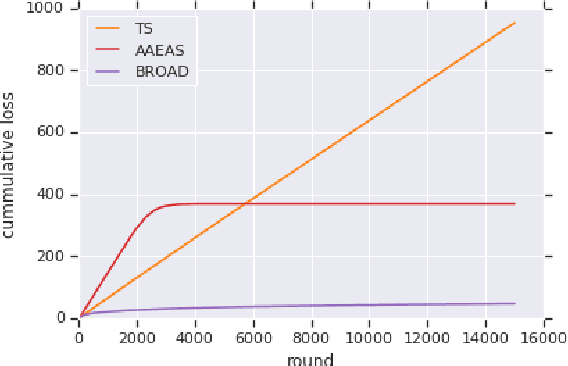
We study "adversarial scaling", a multi-armed bandit model where rewards have a stochastic and an adversarial component. Our model captures display advertising where the "click-through-rate" can be decomposed to a (fixed across time) arm-quality component and a non-stochastic user-relevance component (fixed across arms). Despite the relative stochasticity of our model, we demonstrate two settings where most bandit algorithms suffer. On the positive side, we show that two algorithms, one from the action elimination and one from the mirror descent family are adaptive enough to be robust to adversarial scaling. Our results shed light on the robustness of adaptive parameter selection in stochastic bandits, which may be of independent interest.

Corrupted Multidimensional Binary Search: Learning in the Presence of Irrational Agents

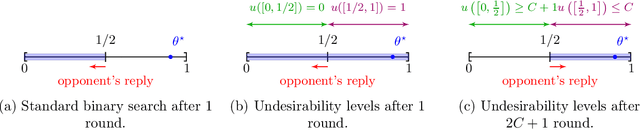
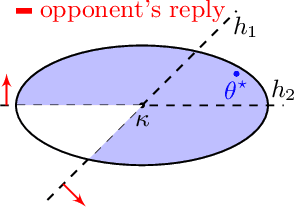
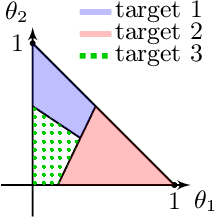
Standard game-theoretic formulations for settings like contextual pricing and security games assume that agents act in accordance with a specific behavioral model. In practice however, some agents may not prescribe to the dominant behavioral model or may act in ways that are arbitrarily inconsistent. Existing algorithms heavily depend on the model being (approximately) accurate for all agents and have poor performance in the presence of even a few such arbitrarily irrational agents. How do we design learning algorithms that are robust to the presence of arbitrarily irrational agents? We address this question for a number of canonical game-theoretic applications by designing a robust algorithm for the fundamental problem of multidimensional binary search. The performance of our algorithm degrades gracefully with the number of corrupted rounds, which correspond to irrational agents and need not be known in advance. As binary search is the key primitive in algorithms for contextual pricing, Stackelberg Security Games, and other game-theoretic applications, we immediately obtain robust algorithms for these settings. Our techniques draw inspiration from learning theory, game theory, high-dimensional geometry, and convex analysis, and may be of independent algorithmic interest.