Incentivizing Desirable Effort Profiles in Strategic Classification: The Role of Causality and Uncertainty

We study strategic classification in binary decision-making settings where agents can modify their features in order to improve their classification outcomes. Importantly, our work considers the causal structure across different features, acknowledging that effort in a given feature may affect other features. The main goal of our work is to understand \emph{when and how much agent effort is invested towards desirable features}, and how this is influenced by the deployed classifier, the causal structure of the agent's features, their ability to modify them, and the information available to the agent about the classifier and the feature causal graph. In the complete information case, when agents know the classifier and the causal structure of the problem, we derive conditions ensuring that rational agents focus on features favored by the principal. We show that designing classifiers to induce desirable behavior is generally non-convex, though tractable in special cases. We also extend our analysis to settings where agents have incomplete information about the classifier or the causal graph. While optimal effort selection is again a non-convex problem under general uncertainty, we highlight special cases of partial uncertainty where this selection problem becomes tractable. Our results indicate that uncertainty drives agents to favor features with higher expected importance and lower variance, potentially misaligning with principal preferences. Finally, numerical experiments based on a cardiovascular disease risk study illustrate how to incentivize desirable modifications under uncertainty.

Online Scheduling for LLM Inference with KV Cache Constraints

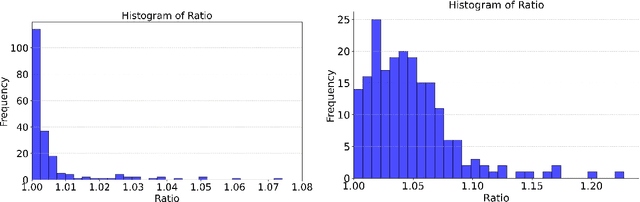
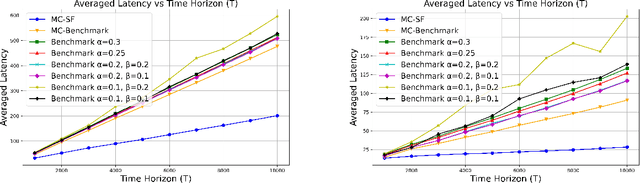
Large Language Model (LLM) inference, where a trained model generates text one word at a time in response to user prompts, is a computationally intensive process requiring efficient scheduling to optimize latency and resource utilization. A key challenge in LLM inference is the management of the Key-Value (KV) cache, which reduces redundant computations but introduces memory constraints. In this work, we model LLM inference with KV cache constraints theoretically and propose novel batching and scheduling algorithms that minimize inference latency while effectively managing the KV cache's memory. We analyze both semi-online and fully online scheduling models, and our results are threefold. First, we provide a polynomial-time algorithm that achieves exact optimality in terms of average latency in the semi-online prompt arrival model. Second, in the fully online case with a stochastic prompt arrival, we introduce an efficient online scheduling algorithm with constant regret. Third, we prove that no algorithm (deterministic or randomized) can achieve a constant competitive ratio in fully online adversarial settings. Our empirical evaluations on a public LLM inference dataset, using the Llama-70B model on A100 GPUs, show that our approach significantly outperforms benchmark algorithms used currently in practice, achieving lower latency while reducing energy consumption. Overall, our results offer a path toward more sustainable and cost-effective LLM deployment.

Is Knowledge Power? On the (Im)possibility of Learning from Strategic Interaction

When learning in strategic environments, a key question is whether agents can overcome uncertainty about their preferences to achieve outcomes they could have achieved absent any uncertainty. Can they do this solely through interactions with each other? We focus this question on the ability of agents to attain the value of their Stackelberg optimal strategy and study the impact of information asymmetry. We study repeated interactions in fully strategic environments where players' actions are decided based on learning algorithms that take into account their observed histories and knowledge of the game. We study the pure Nash equilibria (PNE) of a meta-game where players choose these algorithms as their actions. We demonstrate that if one player has perfect knowledge about the game, then any initial informational gap persists. That is, while there is always a PNE in which the informed agent achieves her Stackelberg value, there is a game where no PNE of the meta-game allows the partially informed player to achieve her Stackelberg value. On the other hand, if both players start with some uncertainty about the game, the quality of information alone does not determine which agent can achieve her Stackelberg value. In this case, the concept of information asymmetry becomes nuanced and depends on the game's structure. Overall, our findings suggest that repeated strategic interactions alone cannot facilitate learning effectively enough to earn an uninformed player her Stackelberg value.

Can Probabilistic Feedback Drive User Impacts in Online Platforms?

A common explanation for negative user impacts of content recommender systems is misalignment between the platform's objective and user welfare. In this work, we show that misalignment in the platform's objective is not the only potential cause of unintended impacts on users: even when the platform's objective is fully aligned with user welfare, the platform's learning algorithm can induce negative downstream impacts on users. The source of these user impacts is that different pieces of content may generate observable user reactions (feedback information) at different rates; these feedback rates may correlate with content properties, such as controversiality or demographic similarity of the creator, that affect the user experience. Since differences in feedback rates can impact how often the learning algorithm engages with different content, the learning algorithm may inadvertently promote content with certain such properties. Using the multi-armed bandit framework with probabilistic feedback, we examine the relationship between feedback rates and a learning algorithm's engagement with individual arms for different no-regret algorithms. We prove that no-regret algorithms can exhibit a wide range of dependencies: if the feedback rate of an arm increases, some no-regret algorithms engage with the arm more, some no-regret algorithms engage with the arm less, and other no-regret algorithms engage with the arm approximately the same number of times. From a platform design perspective, our results highlight the importance of looking beyond regret when measuring an algorithm's performance, and assessing the nature of a learning algorithm's engagement with different types of content as well as their resulting downstream impacts.

Bandits with Deterministically Evolving States

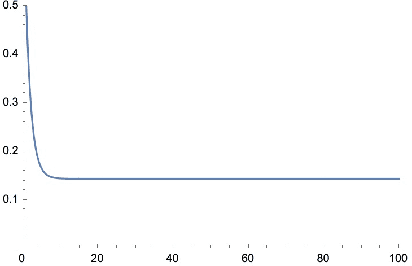
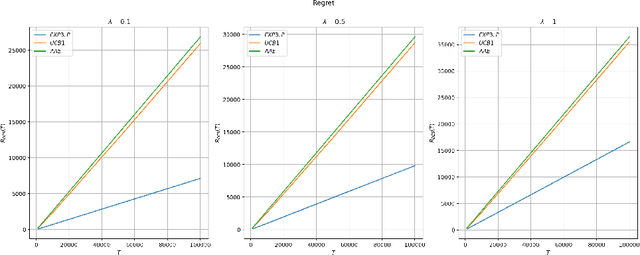
We propose a model for learning with bandit feedback while accounting for deterministically evolving and unobservable states that we call Bandits with Deterministically Evolving States. The workhorse applications of our model are learning for recommendation systems and learning for online ads. In both cases, the reward that the algorithm obtains at each round is a function of the short-term reward of the action chosen and how ``healthy'' the system is (i.e., as measured by its state). For example, in recommendation systems, the reward that the platform obtains from a user's engagement with a particular type of content depends not only on the inherent features of the specific content, but also on how the user's preferences have evolved as a result of interacting with other types of content on the platform. Our general model accounts for the different rate $\lambda \in [0,1]$ at which the state evolves (e.g., how fast a user's preferences shift as a result of previous content consumption) and encompasses standard multi-armed bandits as a special case. The goal of the algorithm is to minimize a notion of regret against the best-fixed sequence of arms pulled. We analyze online learning algorithms for any possible parametrization of the evolution rate $\lambda$. Specifically, the regret rates obtained are: for $\lambda \in [0, 1/T^2]$: $\widetilde O(\sqrt{KT})$; for $\lambda = T^{-a/b}$ with $b < a < 2b$: $\widetilde O (T^{b/a})$; for $\lambda \in (1/T, 1 - 1/\sqrt{T}): \widetilde O (K^{1/3}T^{2/3})$; and for $\lambda \in [1 - 1/\sqrt{T}, 1]: \widetilde O (K\sqrt{T})$.

Strategic Apple Tasting

Algorithmic decision-making in high-stakes domains often involves assigning decisions to agents with incentives to strategically modify their input to the algorithm. In addition to dealing with incentives, in many domains of interest (e.g. lending and hiring) the decision-maker only observes feedback regarding their policy for rounds in which they assign a positive decision to the agent; this type of feedback is often referred to as apple tasting (or one-sided) feedback. We formalize this setting as an online learning problem with apple-tasting feedback where a principal makes decisions about a sequence of $T$ agents, each of which is represented by a context that may be strategically modified. Our goal is to achieve sublinear strategic regret, which compares the performance of the principal to that of the best fixed policy in hindsight, if the agents were truthful when revealing their contexts. Our main result is a learning algorithm which incurs $\tilde{\mathcal{O}}(\sqrt{T})$ strategic regret when the sequence of agents is chosen stochastically. We also give an algorithm capable of handling adversarially-chosen agents, albeit at the cost of $\tilde{\mathcal{O}}(T^{(d+1)/(d+2)})$ strategic regret (where $d$ is the dimension of the context). Our algorithms can be easily adapted to the setting where the principal receives bandit feedback -- this setting generalizes both the linear contextual bandit problem (by considering agents with incentives) and the strategic classification problem (by allowing for partial feedback).

Calibrated Stackelberg Games: Learning Optimal Commitments Against Calibrated Agents

In this paper, we introduce a generalization of the standard Stackelberg Games (SGs) framework: Calibrated Stackelberg Games (CSGs). In CSGs, a principal repeatedly interacts with an agent who (contrary to standard SGs) does not have direct access to the principal's action but instead best-responds to calibrated forecasts about it. CSG is a powerful modeling tool that goes beyond assuming that agents use ad hoc and highly specified algorithms for interacting in strategic settings and thus more robustly addresses real-life applications that SGs were originally intended to capture. Along with CSGs, we also introduce a stronger notion of calibration, termed adaptive calibration, that provides fine-grained any-time calibration guarantees against adversarial sequences. We give a general approach for obtaining adaptive calibration algorithms and specialize them for finite CSGs. In our main technical result, we show that in CSGs, the principal can achieve utility that converges to the optimum Stackelberg value of the game both in finite and continuous settings, and that no higher utility is achievable. Two prominent and immediate applications of our results are the settings of learning in Stackelberg Security Games and strategic classification, both against calibrated agents.

Recommending to Strategic Users

Recommendation systems are pervasive in the digital economy. An important assumption in many deployed systems is that user consumption reflects user preferences in a static sense: users consume the content they like with no other considerations in mind. However, as we document in a large-scale online survey, users do choose content strategically to influence the types of content they get recommended in the future. We model this user behavior as a two-stage noisy signalling game between the recommendation system and users: the recommendation system initially commits to a recommendation policy, presents content to the users during a cold start phase which the users choose to strategically consume in order to affect the types of content they will be recommended in a recommendation phase. We show that in equilibrium, users engage in behaviors that accentuate their differences to users of different preference profiles. In addition, (statistical) minorities out of fear of losing their minority content exposition may not consume content that is liked by mainstream users. We next propose three interventions that may improve recommendation quality (both on average and for minorities) when taking into account strategic consumption: (1) Adopting a recommendation system policy that uses preferences from a prior, (2) Communicating to users that universally liked ("mainstream") content will not be used as basis of recommendation, and (3) Serving content that is personalized-enough yet expected to be liked in the beginning. Finally, we describe a methodology to inform applied theory modeling with survey results.

Strategyproof Decision-Making in Panel Data Settings and Beyond

We propose a framework for decision-making in the presence of strategic agents with panel data, a standard setting in econometrics and statistics where one gets noisy, repeated measurements of multiple units. We consider a setup where there is a pre-intervention period, when the principal observes the outcomes of each unit, after which the principal uses these observations to assign treatment to each unit. Our model can be thought of as a generalization of the synthetic controls and synthetic interventions frameworks, where units (or agents) may strategically manipulate pre-intervention outcomes to receive a more desirable intervention. We identify necessary and sufficient conditions under which a strategyproof mechanism that assigns interventions in the post-intervention period exists. Under a latent factor model assumption, we show that whenever a strategyproof mechanism exists, there is one with a simple closed form. In the setting where there is a single treatment and control (i.e., no other interventions), we establish that there is always a strategyproof mechanism, and provide an algorithm for learning such a mechanism. For the setting of multiple interventions, we provide an algorithm for learning a strategyproof mechanism, if there exists a sufficiently large gap in rewards between the different interventions. Along the way, we prove impossibility results for multi-class strategic classification, which may be of independent interest.

Corruption-Robust Contextual Search through Density Updates

We study the problem of contextual search in the adversarial noise model. Let $d$ be the dimension of the problem, $T$ be the time horizon and $C$ be the total amount of noise in the system. For the $\eps$-ball loss, we give a tight regret bound of $O(C + d \log(1/\eps))$ improving over the $O(d^3 \log(1/\eps)) \log^2(T) + C \log(T) \log(1/\eps))$ bound of Krishnamurthy et al (STOC21). For the symmetric loss, we give an efficient algorithm with regret $O(C+d \log T)$. Our techniques are a significant departure from prior approaches. Specifically, we keep track of density functions over the candidate vectors instead of a knowledge set consisting of the candidate vectors consistent with the feedback obtained.