Incentivizing Desirable Effort Profiles in Strategic Classification: The Role of Causality and Uncertainty

We study strategic classification in binary decision-making settings where agents can modify their features in order to improve their classification outcomes. Importantly, our work considers the causal structure across different features, acknowledging that effort in a given feature may affect other features. The main goal of our work is to understand \emph{when and how much agent effort is invested towards desirable features}, and how this is influenced by the deployed classifier, the causal structure of the agent's features, their ability to modify them, and the information available to the agent about the classifier and the feature causal graph. In the complete information case, when agents know the classifier and the causal structure of the problem, we derive conditions ensuring that rational agents focus on features favored by the principal. We show that designing classifiers to induce desirable behavior is generally non-convex, though tractable in special cases. We also extend our analysis to settings where agents have incomplete information about the classifier or the causal graph. While optimal effort selection is again a non-convex problem under general uncertainty, we highlight special cases of partial uncertainty where this selection problem becomes tractable. Our results indicate that uncertainty drives agents to favor features with higher expected importance and lower variance, potentially misaligning with principal preferences. Finally, numerical experiments based on a cardiovascular disease risk study illustrate how to incentivize desirable modifications under uncertainty.

Differentially Private Data Release on Graphs: Inefficiencies and Unfairness

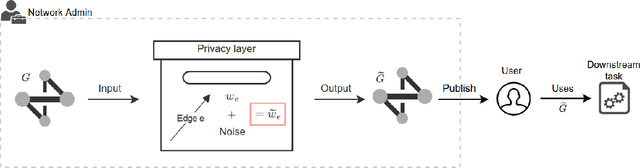
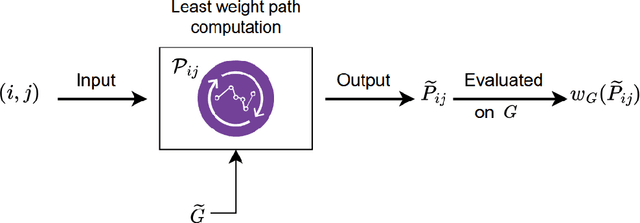
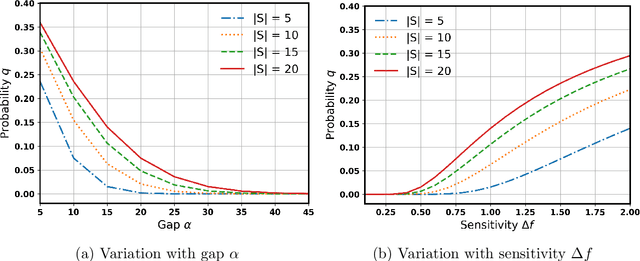
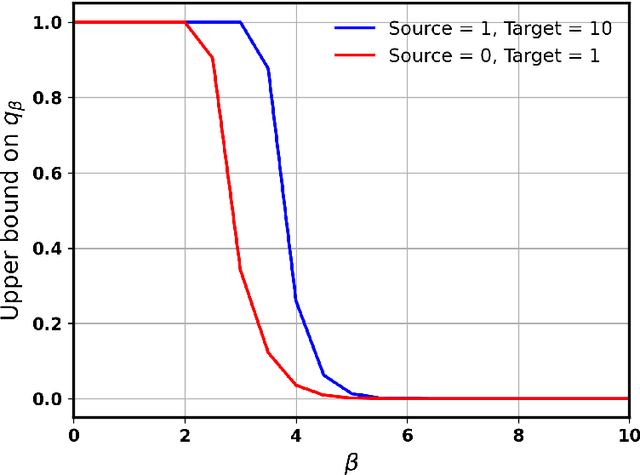
Networks are crucial components of many sectors, including telecommunications, healthcare, finance, energy, and transportation.The information carried in such networks often contains sensitive user data, like location data for commuters and packet data for online users. Therefore, when considering data release for networks, one must ensure that data release mechanisms do not leak information about individuals, quantified in a precise mathematical sense. Differential Privacy (DP) is the widely accepted, formal, state-of-the-art technique, which has found use in a variety of real-life settings including the 2020 U.S. Census, Apple users' device data, or Google's location data. Yet, the use of DP comes with new challenges, as the noise added for privacy introduces inaccuracies or biases and further, DP techniques can also distribute these biases disproportionately across different populations, inducing fairness issues. The goal of this paper is to characterize the impact of DP on bias and unfairness in the context of releasing information about networks, taking a departure from previous work which has studied these effects in the context of private population counts release (such as in the U.S. Census). To this end, we consider a network release problem where the network structure is known to all, but the weights on edges must be released privately. We consider the impact of this private release on a simple downstream decision-making task run by a third-party, which is to find the shortest path between any two pairs of nodes and recommend the best route to users. This setting is of highly practical relevance, mirroring scenarios in transportation networks, where preserving privacy while providing accurate routing information is crucial. Our work provides theoretical foundations and empirical evidence into the bias and unfairness arising due to privacy in these networked decision problems.