KL-regularization Itself is Differentially Private in Bandits and RLHF

Differential Privacy (DP) provides a rigorous framework for privacy, ensuring the outputs of data-driven algorithms remain statistically indistinguishable across datasets that differ in a single entry. While guaranteeing DP generally requires explicitly injecting noise either to the algorithm itself or to its outputs, the intrinsic randomness of existing algorithms presents an opportunity to achieve DP ``for free''. In this work, we explore the role of regularization in achieving DP across three different decision-making problems: multi-armed bandits, linear contextual bandits, and reinforcement learning from human feedback (RLHF), in offline data settings. We show that adding KL-regularization to the learning objective (a common approach in optimization algorithms) makes the action sampled from the resulting stochastic policy itself differentially private. This offers a new route to privacy guarantees without additional noise injection, while also preserving the inherent advantage of regularization in enhancing performance.

Optimal Allocation of Privacy Budget on Hierarchical Data Release

Releasing useful information from datasets with hierarchical structures while preserving individual privacy presents a significant challenge. Standard privacy-preserving mechanisms, and in particular Differential Privacy, often require careful allocation of a finite privacy budget across different levels and components of the hierarchy. Sub-optimal allocation can lead to either excessive noise, rendering the data useless, or to insufficient protections for sensitive information. This paper addresses the critical problem of optimal privacy budget allocation for hierarchical data release. It formulates this challenge as a constrained optimization problem, aiming to maximize data utility subject to a total privacy budget while considering the inherent trade-offs between data granularity and privacy loss. The proposed approach is supported by theoretical analysis and validated through comprehensive experiments on real hierarchical datasets. These experiments demonstrate that optimal privacy budget allocation significantly enhances the utility of the released data and improves the performance of downstream tasks.

Multi-Agent Performative Prediction Beyond the Insensitivity Assumption: A Case Study for Mortgage Competition

Performative prediction models account for feedback loops in decision-making processes where predictions influence future data distributions. While existing work largely assumes insensitivity of data distributions to small strategy changes, this assumption usually fails in real-world competitive (i.e. multi-agent) settings. For example, in Bertrand-type competitions, a small reduction in one firm's price can lead that firm to capture the entire demand, while all others sharply lose all of their customers. We study a representative setting of multi-agent performative prediction in which insensitivity assumptions do not hold, and investigate the convergence of natural dynamics. To do so, we focus on a specific game that we call the ''Bank Game'', where two lenders compete over interest rates and credit score thresholds. Consumers act similarly as to in a Bertrand Competition, with each consumer selecting the firm with the lowest interest rate that they are eligible for based on the firms' credit thresholds. Our analysis characterizes the equilibria of this game and demonstrates that when both firms use a common and natural no-regret learning dynamic -- exponential weights -- with proper initialization, the dynamics always converge to stable outcomes despite the general-sum structure. Notably, our setting admits multiple stable equilibria, with convergence dependent on initial conditions. We also provide theoretical convergence results in the stochastic case when the utility matrix is not fully known, but each learner can observe sufficiently many samples of consumers at each time step to estimate it, showing robustness to slight mis-specifications. Finally, we provide experimental results that validate our theoretical findings.

Incentivizing Desirable Effort Profiles in Strategic Classification: The Role of Causality and Uncertainty

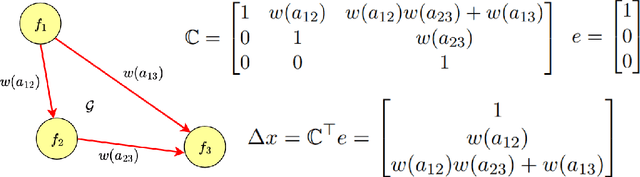
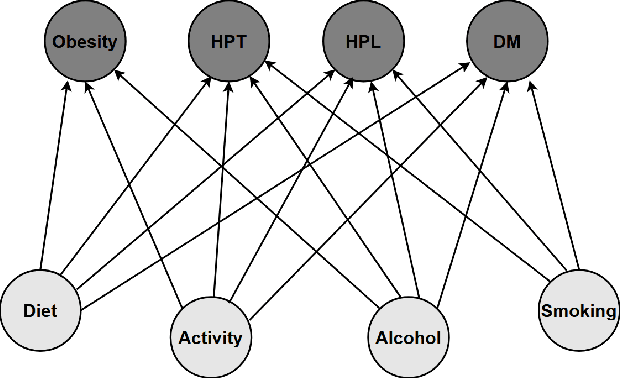
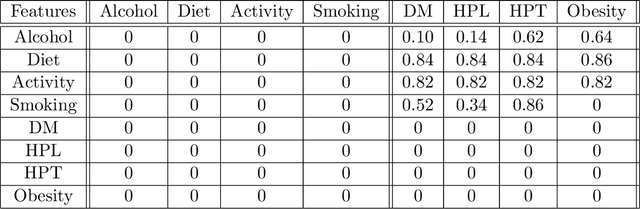
We study strategic classification in binary decision-making settings where agents can modify their features in order to improve their classification outcomes. Importantly, our work considers the causal structure across different features, acknowledging that effort in a given feature may affect other features. The main goal of our work is to understand \emph{when and how much agent effort is invested towards desirable features}, and how this is influenced by the deployed classifier, the causal structure of the agent's features, their ability to modify them, and the information available to the agent about the classifier and the feature causal graph. In the complete information case, when agents know the classifier and the causal structure of the problem, we derive conditions ensuring that rational agents focus on features favored by the principal. We show that designing classifiers to induce desirable behavior is generally non-convex, though tractable in special cases. We also extend our analysis to settings where agents have incomplete information about the classifier or the causal graph. While optimal effort selection is again a non-convex problem under general uncertainty, we highlight special cases of partial uncertainty where this selection problem becomes tractable. Our results indicate that uncertainty drives agents to favor features with higher expected importance and lower variance, potentially misaligning with principal preferences. Finally, numerical experiments based on a cardiovascular disease risk study illustrate how to incentivize desirable modifications under uncertainty.

Differential Privacy Overview and Fundamental Techniques

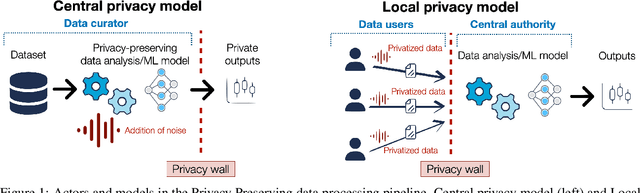
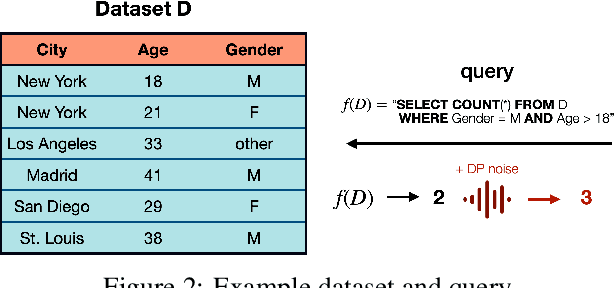
This chapter is meant to be part of the book "Differential Privacy in Artificial Intelligence: From Theory to Practice" and provides an introduction to Differential Privacy. It starts by illustrating various attempts to protect data privacy, emphasizing where and why they failed, and providing the key desiderata of a robust privacy definition. It then defines the key actors, tasks, and scopes that make up the domain of privacy-preserving data analysis. Following that, it formalizes the definition of Differential Privacy and its inherent properties, including composition, post-processing immunity, and group privacy. The chapter also reviews the basic techniques and mechanisms commonly used to implement Differential Privacy in its pure and approximate forms.

Algorithmic Collusion Without Threats

There has been substantial recent concern that pricing algorithms might learn to ``collude.'' Supra-competitive prices can emerge as a Nash equilibrium of repeated pricing games, in which sellers play strategies which threaten to punish their competitors who refuse to support high prices, and these strategies can be automatically learned. In fact, a standard economic intuition is that supra-competitive prices emerge from either the use of threats, or a failure of one party to optimize their payoff. Is this intuition correct? Would preventing threats in algorithmic decision-making prevent supra-competitive prices when sellers are optimizing for their own revenue? No. We show that supra-competitive prices can emerge even when both players are using algorithms which do not encode threats, and which optimize for their own revenue. We study sequential pricing games in which a first mover deploys an algorithm and then a second mover optimizes within the resulting environment. We show that if the first mover deploys any algorithm with a no-regret guarantee, and then the second mover even approximately optimizes within this now static environment, monopoly-like prices arise. The result holds for any no-regret learning algorithm deployed by the first mover and for any pricing policy of the second mover that obtains them profit at least as high as a random pricing would -- and hence the result applies even when the second mover is optimizing only within a space of non-responsive pricing distributions which are incapable of encoding threats. In fact, there exists a set of strategies, neither of which explicitly encode threats that form a Nash equilibrium of the simultaneous pricing game in algorithm space, and lead to near monopoly prices. This suggests that the definition of ``algorithmic collusion'' may need to be expanded, to include strategies without explicitly encoded threats.

Fairness Issues and Mitigations in (Differentially Private) Socio-demographic Data Processes

Statistical agencies rely on sampling techniques to collect socio-demographic data crucial for policy-making and resource allocation. This paper shows that surveys of important societal relevance introduce sampling errors that unevenly impact group-level estimates, thereby compromising fairness in downstream decisions. To address these issues, this paper introduces an optimization approach modeled on real-world survey design processes, ensuring sampling costs are optimized while maintaining error margins within prescribed tolerances. Additionally, privacy-preserving methods used to determine sampling rates can further impact these fairness issues. The paper explores the impact of differential privacy on the statistics informing the sampling process, revealing a surprising effect: not only the expected negative effect from the addition of noise for differential privacy is negligible, but also this privacy noise can in fact reduce unfairness as it positively biases smaller counts. These findings are validated over an extensive analysis using datasets commonly applied in census statistics.

Differentially Private Data Release on Graphs: Inefficiencies and Unfairness

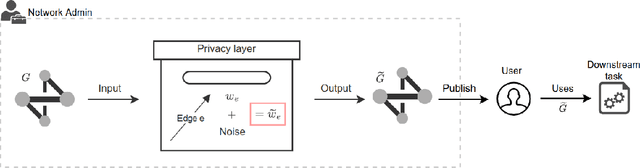
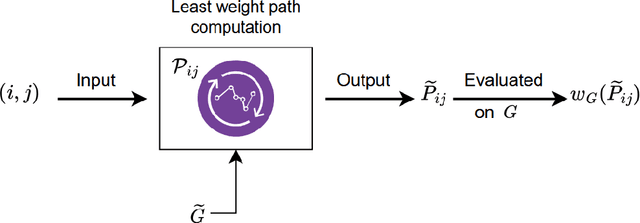
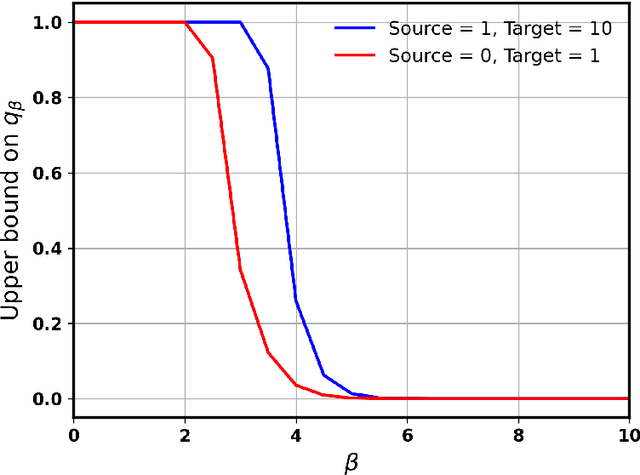
Networks are crucial components of many sectors, including telecommunications, healthcare, finance, energy, and transportation.The information carried in such networks often contains sensitive user data, like location data for commuters and packet data for online users. Therefore, when considering data release for networks, one must ensure that data release mechanisms do not leak information about individuals, quantified in a precise mathematical sense. Differential Privacy (DP) is the widely accepted, formal, state-of-the-art technique, which has found use in a variety of real-life settings including the 2020 U.S. Census, Apple users' device data, or Google's location data. Yet, the use of DP comes with new challenges, as the noise added for privacy introduces inaccuracies or biases and further, DP techniques can also distribute these biases disproportionately across different populations, inducing fairness issues. The goal of this paper is to characterize the impact of DP on bias and unfairness in the context of releasing information about networks, taking a departure from previous work which has studied these effects in the context of private population counts release (such as in the U.S. Census). To this end, we consider a network release problem where the network structure is known to all, but the weights on edges must be released privately. We consider the impact of this private release on a simple downstream decision-making task run by a third-party, which is to find the shortest path between any two pairs of nodes and recommend the best route to users. This setting is of highly practical relevance, mirroring scenarios in transportation networks, where preserving privacy while providing accurate routing information is crucial. Our work provides theoretical foundations and empirical evidence into the bias and unfairness arising due to privacy in these networked decision problems.

Bayesian Strategic Classification

In strategic classification, agents modify their features, at a cost, to ideally obtain a positive classification from the learner's classifier. The typical response of the learner is to carefully modify their classifier to be robust to such strategic behavior. When reasoning about agent manipulations, most papers that study strategic classification rely on the following strong assumption: agents fully know the exact parameters of the deployed classifier by the learner. This often is an unrealistic assumption when using complex or proprietary machine learning techniques in real-world prediction tasks. We initiate the study of partial information release by the learner in strategic classification. We move away from the traditional assumption that agents have full knowledge of the classifier. Instead, we consider agents that have a common distributional prior on which classifier the learner is using. The learner in our model can reveal truthful, yet not necessarily complete, information about the deployed classifier to the agents. The learner's goal is to release just enough information about the classifier to maximize accuracy. We show how such partial information release can, counter-intuitively, benefit the learner's accuracy, despite increasing agents' abilities to manipulate. We show that while it is intractable to compute the best response of an agent in the general case, there exist oracle-efficient algorithms that can solve the best response of the agents when the learner's hypothesis class is the class of linear classifiers, or when the agents' cost function satisfies a natural notion of submodularity as we define. We then turn our attention to the learner's optimization problem and provide both positive and negative results on the algorithmic problem of how much information the learner should release about the classifier to maximize their expected accuracy.

Personalized Differential Privacy for Ridge Regression

The increased application of machine learning (ML) in sensitive domains requires protecting the training data through privacy frameworks, such as differential privacy (DP). DP requires to specify a uniform privacy level $\varepsilon$ that expresses the maximum privacy loss that each data point in the entire dataset is willing to tolerate. Yet, in practice, different data points often have different privacy requirements. Having to set one uniform privacy level is usually too restrictive, often forcing a learner to guarantee the stringent privacy requirement, at a large cost to accuracy. To overcome this limitation, we introduce our novel Personalized-DP Output Perturbation method (PDP-OP) that enables to train Ridge regression models with individual per data point privacy levels. We provide rigorous privacy proofs for our PDP-OP as well as accuracy guarantees for the resulting model. This work is the first to provide such theoretical accuracy guarantees when it comes to personalized DP in machine learning, whereas previous work only provided empirical evaluations. We empirically evaluate PDP-OP on synthetic and real datasets and with diverse privacy distributions. We show that by enabling each data point to specify their own privacy requirement, we can significantly improve the privacy-accuracy trade-offs in DP. We also show that PDP-OP outperforms the personalized privacy techniques of Jorgensen et al. (2015).