SCaLE: Switching Cost aware Learning and Exploration

This work addresses the fundamental problem of unbounded metric movement costs in bandit online convex optimization, by considering high-dimensional dynamic quadratic hitting costs and $\ell_2$-norm switching costs in a noisy bandit feedback model. For a general class of stochastic environments, we provide the first algorithm SCaLE that provably achieves a distribution-agnostic sub-linear dynamic regret, without the knowledge of hitting cost structure. En-route, we present a novel spectral regret analysis that separately quantifies eigenvalue-error driven regret and eigenbasis-perturbation driven regret. Extensive numerical experiments, against online-learning baselines, corroborate our claims, and highlight statistical consistency of our algorithm.

Fairness-Regularized Online Optimization with Switching Costs

Fairness and action smoothness are two crucial considerations in many online optimization problems, but they have yet to be addressed simultaneously. In this paper, we study a new and challenging setting of fairness-regularized smoothed online convex optimization with switching costs. First, to highlight the fundamental challenges introduced by the long-term fairness regularizer evaluated based on the entire sequence of actions, we prove that even without switching costs, no online algorithms can possibly achieve a sublinear regret or finite competitive ratio compared to the offline optimal algorithm as the problem episode length $T$ increases. Then, we propose FairOBD (Fairness-regularized Online Balanced Descent), which reconciles the tension between minimizing the hitting cost, switching cost, and fairness cost. Concretely, FairOBD decomposes the long-term fairness cost into a sequence of online costs by introducing an auxiliary variable and then leverages the auxiliary variable to regularize the online actions for fair outcomes. Based on a new approach to account for switching costs, we prove that FairOBD offers a worst-case asymptotic competitive ratio against a novel benchmark -- the optimal offline algorithm with parameterized constraints -- by considering $T\to\infty$. Finally, we run trace-driven experiments of dynamic computing resource provisioning for socially responsible AI inference to empirically evaluate FairOBD, showing that FairOBD can effectively reduce the total fairness-regularized cost and better promote fair outcomes compared to existing baseline solutions.

Efficient Policy Optimization in Robust Constrained MDPs with Iteration Complexity Guarantees

Constrained decision-making is essential for designing safe policies in real-world control systems, yet simulated environments often fail to capture real-world adversities. We consider the problem of learning a policy that will maximize the cumulative reward while satisfying a constraint, even when there is a mismatch between the real model and an accessible simulator/nominal model. In particular, we consider the robust constrained Markov decision problem (RCMDP) where an agent needs to maximize the reward and satisfy the constraint against the worst possible stochastic model under the uncertainty set centered around an unknown nominal model. Primal-dual methods, effective for standard constrained MDP (CMDP), are not applicable here because of the lack of the strong duality property. Further, one cannot apply the standard robust value-iteration based approach on the composite value function either as the worst case models may be different for the reward value function and the constraint value function. We propose a novel technique that effectively minimizes the constraint value function--to satisfy the constraints; on the other hand, when all the constraints are satisfied, it can simply maximize the robust reward value function. We prove that such an algorithm finds a policy with at most $\epsilon$ sub-optimality and feasible policy after $O(\epsilon^{-2})$ iterations. In contrast to the state-of-the-art method, we do not need to employ a binary search, thus, we reduce the computation time by at least 4x for smaller value of discount factor ($\gamma$) and by at least 6x for larger value of $\gamma$.

KL-regularization Itself is Differentially Private in Bandits and RLHF

Differential Privacy (DP) provides a rigorous framework for privacy, ensuring the outputs of data-driven algorithms remain statistically indistinguishable across datasets that differ in a single entry. While guaranteeing DP generally requires explicitly injecting noise either to the algorithm itself or to its outputs, the intrinsic randomness of existing algorithms presents an opportunity to achieve DP ``for free''. In this work, we explore the role of regularization in achieving DP across three different decision-making problems: multi-armed bandits, linear contextual bandits, and reinforcement learning from human feedback (RLHF), in offline data settings. We show that adding KL-regularization to the learning objective (a common approach in optimization algorithms) makes the action sampled from the resulting stochastic policy itself differentially private. This offers a new route to privacy guarantees without additional noise injection, while also preserving the inherent advantage of regularization in enhancing performance.

Fusing Reward and Dueling Feedback in Stochastic Bandits

This paper investigates the fusion of absolute (reward) and relative (dueling) feedback in stochastic bandits, where both feedback types are gathered in each decision round. We derive a regret lower bound, demonstrating that an efficient algorithm may incur only the smaller among the reward and dueling-based regret for each individual arm. We propose two fusion approaches: (1) a simple elimination fusion algorithm that leverages both feedback types to explore all arms and unifies collected information by sharing a common candidate arm set, and (2) a decomposition fusion algorithm that selects the more effective feedback to explore the corresponding arms and randomly assigns one feedback type for exploration and the other for exploitation in each round. The elimination fusion experiences a suboptimal multiplicative term of the number of arms in regret due to the intrinsic suboptimality of dueling elimination. In contrast, the decomposition fusion achieves regret matching the lower bound up to a constant under a common assumption. Extensive experiments confirm the efficacy of our algorithms and theoretical results.

Robust Gymnasium: A Unified Modular Benchmark for Robust Reinforcement Learning

Driven by inherent uncertainty and the sim-to-real gap, robust reinforcement learning (RL) seeks to improve resilience against the complexity and variability in agent-environment sequential interactions. Despite the existence of a large number of RL benchmarks, there is a lack of standardized benchmarks for robust RL. Current robust RL policies often focus on a specific type of uncertainty and are evaluated in distinct, one-off environments. In this work, we introduce Robust-Gymnasium, a unified modular benchmark designed for robust RL that supports a wide variety of disruptions across all key RL components-agents' observed state and reward, agents' actions, and the environment. Offering over sixty diverse task environments spanning control and robotics, safe RL, and multi-agent RL, it provides an open-source and user-friendly tool for the community to assess current methods and foster the development of robust RL algorithms. In addition, we benchmark existing standard and robust RL algorithms within this framework, uncovering significant deficiencies in each and offering new insights.

Towards Environmentally Equitable AI

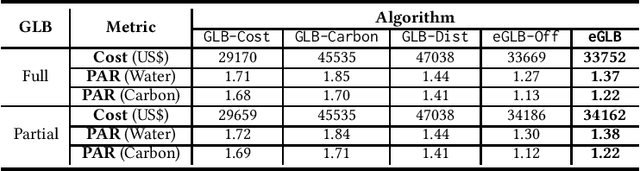
The skyrocketing demand for artificial intelligence (AI) has created an enormous appetite for globally deployed power-hungry servers. As a result, the environmental footprint of AI systems has come under increasing scrutiny. More crucially, the current way that we exploit AI workloads' flexibility and manage AI systems can lead to wildly different environmental impacts across locations, increasingly raising environmental inequity concerns and creating unintended sociotechnical consequences. In this paper, we advocate environmental equity as a priority for the management of future AI systems, advancing the boundaries of existing resource management for sustainable AI and also adding a unique dimension to AI fairness. Concretely, we uncover the potential of equity-aware geographical load balancing to fairly re-distribute the environmental cost across different regions, followed by algorithmic challenges. We conclude by discussing a few future directions to exploit the full potential of system management approaches to mitigate AI's environmental inequity.

Communication Efficient Decentralization for Smoothed Online Convex Optimization

We study the multi-agent Smoothed Online Convex Optimization (SOCO) problem, where $N$ agents interact through a communication graph. In each round, each agent $i$ receives a strongly convex hitting cost function $f^i_t$ in an online fashion and selects an action $x^i_t \in \mathbb{R}^d$. The objective is to minimize the global cumulative cost, which includes the sum of individual hitting costs $f^i_t(x^i_t)$, a temporal "switching cost" for changing decisions, and a spatial "dissimilarity cost" that penalizes deviations in decisions among neighboring agents. We propose the first decentralized algorithm for multi-agent SOCO and prove its asymptotic optimality. Our approach allows each agent to operate using only local information from its immediate neighbors in the graph. For finite-time performance, we establish that the optimality gap in competitive ratio decreases with the time horizon $T$ and can be conveniently tuned based on the per-round computation available to each agent. Moreover, our results hold even when the communication graph changes arbitrarily and adaptively over time. Finally, we establish that the computational complexity per round depends only logarithmically on the number of agents and almost linearly on their degree within the graph, ensuring scalability for large-system implementations.

Safe Exploitative Play with Untrusted Type Beliefs

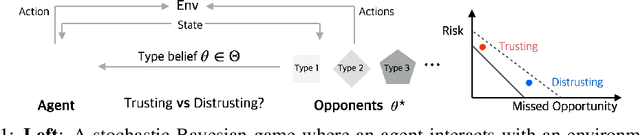
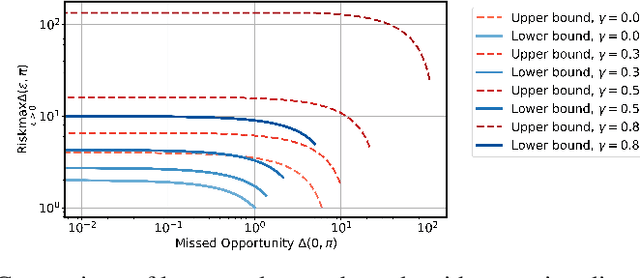
The combination of the Bayesian game and learning has a rich history, with the idea of controlling a single agent in a system composed of multiple agents with unknown behaviors given a set of types, each specifying a possible behavior for the other agents. The idea is to plan an agent's own actions with respect to those types which it believes are most likely to maximize the payoff. However, the type beliefs are often learned from past actions and likely to be incorrect. With this perspective in mind, we consider an agent in a game with type predictions of other components, and investigate the impact of incorrect beliefs to the agent's payoff. In particular, we formally define a tradeoff between risk and opportunity by comparing the payoff obtained against the optimal payoff, which is represented by a gap caused by trusting or distrusting the learned beliefs. Our main results characterize the tradeoff by establishing upper and lower bounds on the Pareto front for both normal-form and stochastic Bayesian games, with numerical results provided.

Hybrid Transfer Reinforcement Learning: Provable Sample Efficiency from Shifted-Dynamics Data

Online Reinforcement learning (RL) typically requires high-stakes online interaction data to learn a policy for a target task. This prompts interest in leveraging historical data to improve sample efficiency. The historical data may come from outdated or related source environments with different dynamics. It remains unclear how to effectively use such data in the target task to provably enhance learning and sample efficiency. To address this, we propose a hybrid transfer RL (HTRL) setting, where an agent learns in a target environment while accessing offline data from a source environment with shifted dynamics. We show that -- without information on the dynamics shift -- general shifted-dynamics data, even with subtle shifts, does not reduce sample complexity in the target environment. However, with prior information on the degree of the dynamics shift, we design HySRL, a transfer algorithm that achieves problem-dependent sample complexity and outperforms pure online RL. Finally, our experimental results demonstrate that HySRL surpasses state-of-the-art online RL baseline.