Evolving Language Models without Labels: Majority Drives Selection, Novelty Promotes Variation

Large language models (LLMs) are increasingly trained with reinforcement learning from verifiable rewards (RLVR), yet real-world deployment demands models that can self-improve without labels or external judges. Existing label-free methods, confidence minimization, self-consistency, or majority-vote objectives, stabilize learning but steadily shrink exploration, causing an entropy collapse: generations become shorter, less diverse, and brittle. Unlike prior approaches such as Test-Time Reinforcement Learning (TTRL), which primarily adapt models to the immediate unlabeled dataset at hand, our goal is broader: to enable general improvements without sacrificing the model's inherent exploration capacity and generalization ability, i.e., evolving. We formalize this issue and propose EVolution-Oriented and Label-free Reinforcement Learning (EVOL-RL), a simple rule that couples stability with variation under a label-free setting. EVOL-RL keeps the majority-voted answer as a stable anchor (selection) while adding a novelty-aware reward that favors responses whose reasoning differs from what has already been produced (variation), measured in semantic space. Implemented with GRPO, EVOL-RL also uses asymmetric clipping to preserve strong signals and an entropy regularizer to sustain search. This majority-for-selection + novelty-for-variation design prevents collapse, maintains longer and more informative chains of thought, and improves both pass@1 and pass@n. EVOL-RL consistently outperforms the majority-only TTRL baseline; e.g., training on label-free AIME24 lifts Qwen3-4B-Base AIME25 pass@1 from TTRL's 4.6% to 16.4%, and pass@16 from 18.5% to 37.9%. EVOL-RL not only prevents diversity collapse but also unlocks stronger generalization across domains (e.g., GPQA). Furthermore, we demonstrate that EVOL-RL also boosts performance in the RLVR setting, highlighting its broad applicability.

TARDIS STRIDE: A Spatio-Temporal Road Image Dataset for Exploration and Autonomy

World models aim to simulate environments and enable effective agent behavior. However, modeling real-world environments presents unique challenges as they dynamically change across both space and, crucially, time. To capture these composed dynamics, we introduce a Spatio-Temporal Road Image Dataset for Exploration (STRIDE) permuting 360-degree panoramic imagery into rich interconnected observation, state and action nodes. Leveraging this structure, we can simultaneously model the relationship between egocentric views, positional coordinates, and movement commands across both space and time. We benchmark this dataset via TARDIS, a transformer-based generative world model that integrates spatial and temporal dynamics through a unified autoregressive framework trained on STRIDE. We demonstrate robust performance across a range of agentic tasks such as controllable photorealistic image synthesis, instruction following, autonomous self-control, and state-of-the-art georeferencing. These results suggest a promising direction towards sophisticated generalist agents--capable of understanding and manipulating the spatial and temporal aspects of their material environments--with enhanced embodied reasoning capabilities. Training code, datasets, and model checkpoints are made available at https://huggingface.co/datasets/Tera-AI/STRIDE.

Efficient Policy Optimization in Robust Constrained MDPs with Iteration Complexity Guarantees

Constrained decision-making is essential for designing safe policies in real-world control systems, yet simulated environments often fail to capture real-world adversities. We consider the problem of learning a policy that will maximize the cumulative reward while satisfying a constraint, even when there is a mismatch between the real model and an accessible simulator/nominal model. In particular, we consider the robust constrained Markov decision problem (RCMDP) where an agent needs to maximize the reward and satisfy the constraint against the worst possible stochastic model under the uncertainty set centered around an unknown nominal model. Primal-dual methods, effective for standard constrained MDP (CMDP), are not applicable here because of the lack of the strong duality property. Further, one cannot apply the standard robust value-iteration based approach on the composite value function either as the worst case models may be different for the reward value function and the constraint value function. We propose a novel technique that effectively minimizes the constraint value function--to satisfy the constraints; on the other hand, when all the constraints are satisfied, it can simply maximize the robust reward value function. We prove that such an algorithm finds a policy with at most $\epsilon$ sub-optimality and feasible policy after $O(\epsilon^{-2})$ iterations. In contrast to the state-of-the-art method, we do not need to employ a binary search, thus, we reduce the computation time by at least 4x for smaller value of discount factor ($\gamma$) and by at least 6x for larger value of $\gamma$.

KL-regularization Itself is Differentially Private in Bandits and RLHF

Differential Privacy (DP) provides a rigorous framework for privacy, ensuring the outputs of data-driven algorithms remain statistically indistinguishable across datasets that differ in a single entry. While guaranteeing DP generally requires explicitly injecting noise either to the algorithm itself or to its outputs, the intrinsic randomness of existing algorithms presents an opportunity to achieve DP ``for free''. In this work, we explore the role of regularization in achieving DP across three different decision-making problems: multi-armed bandits, linear contextual bandits, and reinforcement learning from human feedback (RLHF), in offline data settings. We show that adding KL-regularization to the learning objective (a common approach in optimization algorithms) makes the action sampled from the resulting stochastic policy itself differentially private. This offers a new route to privacy guarantees without additional noise injection, while also preserving the inherent advantage of regularization in enhancing performance.

Distributionally Robust Direct Preference Optimization

A major challenge in aligning large language models (LLMs) with human preferences is the issue of distribution shift. LLM alignment algorithms rely on static preference datasets, assuming that they accurately represent real-world user preferences. However, user preferences vary significantly across geographical regions, demographics, linguistic patterns, and evolving cultural trends. This preference distribution shift leads to catastrophic alignment failures in many real-world applications. We address this problem using the principled framework of distributionally robust optimization, and develop two novel distributionally robust direct preference optimization (DPO) algorithms, namely, Wasserstein DPO (WDPO) and Kullback-Leibler DPO (KLDPO). We characterize the sample complexity of learning the optimal policy parameters for WDPO and KLDPO. Moreover, we propose scalable gradient descent-style learning algorithms by developing suitable approximations for the challenging minimax loss functions of WDPO and KLDPO. Our empirical experiments demonstrate the superior performance of WDPO and KLDPO in substantially improving the alignment when there is a preference distribution shift.

Hybrid Transfer Reinforcement Learning: Provable Sample Efficiency from Shifted-Dynamics Data

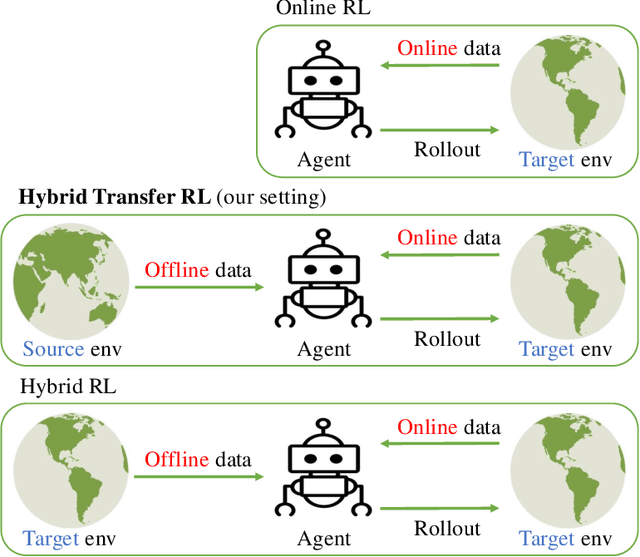
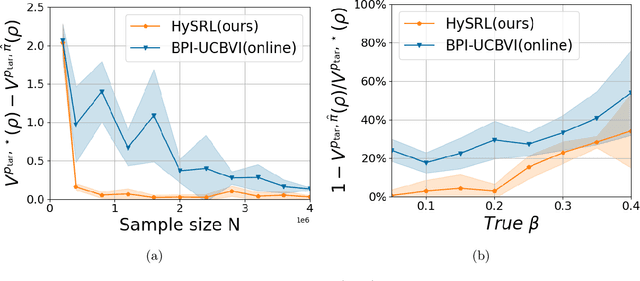
Online Reinforcement learning (RL) typically requires high-stakes online interaction data to learn a policy for a target task. This prompts interest in leveraging historical data to improve sample efficiency. The historical data may come from outdated or related source environments with different dynamics. It remains unclear how to effectively use such data in the target task to provably enhance learning and sample efficiency. To address this, we propose a hybrid transfer RL (HTRL) setting, where an agent learns in a target environment while accessing offline data from a source environment with shifted dynamics. We show that -- without information on the dynamics shift -- general shifted-dynamics data, even with subtle shifts, does not reduce sample complexity in the target environment. However, with prior information on the degree of the dynamics shift, we design HySRL, a transfer algorithm that achieves problem-dependent sample complexity and outperforms pure online RL. Finally, our experimental results demonstrate that HySRL surpasses state-of-the-art online RL baseline.

Distributionally Robust Constrained Reinforcement Learning under Strong Duality

We study the problem of Distributionally Robust Constrained RL (DRC-RL), where the goal is to maximize the expected reward subject to environmental distribution shifts and constraints. This setting captures situations where training and testing environments differ, and policies must satisfy constraints motivated by safety or limited budgets. Despite significant progress toward algorithm design for the separate problems of distributionally robust RL and constrained RL, there do not yet exist algorithms with end-to-end convergence guarantees for DRC-RL. We develop an algorithmic framework based on strong duality that enables the first efficient and provable solution in a class of environmental uncertainties. Further, our framework exposes an inherent structure of DRC-RL that arises from the combination of distributional robustness and constraints, which prevents a popular class of iterative methods from tractably solving DRC-RL, despite such frameworks being applicable for each of distributionally robust RL and constrained RL individually. Finally, we conduct experiments on a car racing benchmark to evaluate the effectiveness of the proposed algorithm.

Tractable Equilibrium Computation in Markov Games through Risk Aversion

A significant roadblock to the development of principled multi-agent reinforcement learning is the fact that desired solution concepts like Nash equilibria may be intractable to compute. To overcome this obstacle, we take inspiration from behavioral economics and show that -- by imbuing agents with important features of human decision-making like risk aversion and bounded rationality -- a class of risk-averse quantal response equilibria (RQE) become tractable to compute in all $n$-player matrix and finite-horizon Markov games. In particular, we show that they emerge as the endpoint of no-regret learning in suitably adjusted versions of the games. Crucially, the class of computationally tractable RQE is independent of the underlying game structure and only depends on agents' degree of risk-aversion and bounded rationality. To validate the richness of this class of solution concepts we show that it captures peoples' patterns of play in a number of 2-player matrix games previously studied in experimental economics. Furthermore, we give a first analysis of the sample complexity of computing these equilibria in finite-horizon Markov games when one has access to a generative model and validate our findings on a simple multi-agent reinforcement learning benchmark.

Model-Free Robust $φ$-Divergence Reinforcement Learning Using Both Offline and Online Data

The robust $\phi$-regularized Markov Decision Process (RRMDP) framework focuses on designing control policies that are robust against parameter uncertainties due to mismatches between the simulator (nominal) model and real-world settings. This work makes two important contributions. First, we propose a model-free algorithm called Robust $\phi$-regularized fitted Q-iteration (RPQ) for learning an $\epsilon$-optimal robust policy that uses only the historical data collected by rolling out a behavior policy (with robust exploratory requirement) on the nominal model. To the best of our knowledge, we provide the first unified analysis for a class of $\phi$-divergences achieving robust optimal policies in high-dimensional systems with general function approximation. Second, we introduce the hybrid robust $\phi$-regularized reinforcement learning framework to learn an optimal robust policy using both historical data and online sampling. Towards this framework, we propose a model-free algorithm called Hybrid robust Total-variation-regularized Q-iteration (HyTQ: pronounced height-Q). To the best of our knowledge, we provide the first improved out-of-data-distribution assumption in large-scale problems with general function approximation under the hybrid robust $\phi$-regularized reinforcement learning framework. Finally, we provide theoretical guarantees on the performance of the learned policies of our algorithms on systems with arbitrary large state space.

Bridging Distributionally Robust Learning and Offline RL: An Approach to Mitigate Distribution Shift and Partial Data Coverage

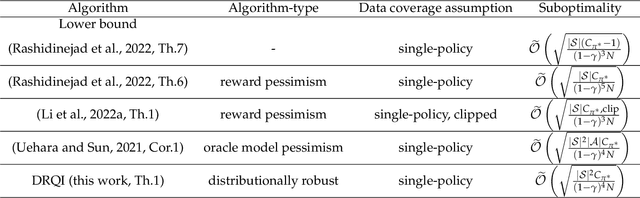
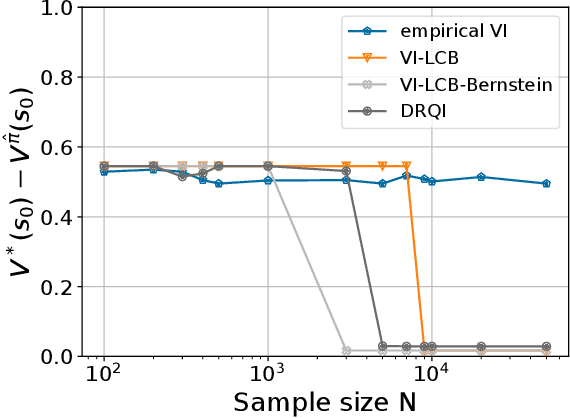
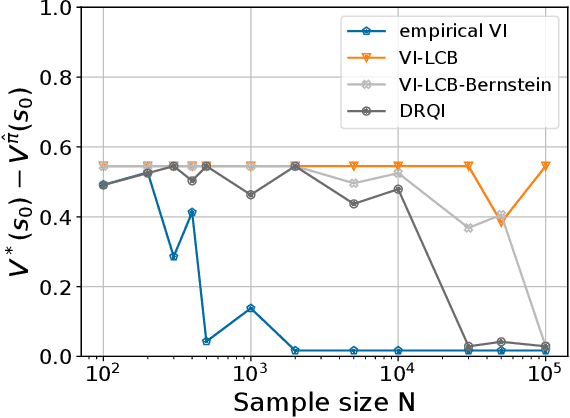
The goal of an offline reinforcement learning (RL) algorithm is to learn optimal polices using historical (offline) data, without access to the environment for online exploration. One of the main challenges in offline RL is the distribution shift which refers to the difference between the state-action visitation distribution of the data generating policy and the learning policy. Many recent works have used the idea of pessimism for developing offline RL algorithms and characterizing their sample complexity under a relatively weak assumption of single policy concentrability. Different from the offline RL literature, the area of distributionally robust learning (DRL) offers a principled framework that uses a minimax formulation to tackle model mismatch between training and testing environments. In this work, we aim to bridge these two areas by showing that the DRL approach can be used to tackle the distributional shift problem in offline RL. In particular, we propose two offline RL algorithms using the DRL framework, for the tabular and linear function approximation settings, and characterize their sample complexity under the single policy concentrability assumption. We also demonstrate the superior performance our proposed algorithm through simulation experiments.