Bridging Distributionally Robust Learning and Offline RL: An Approach to Mitigate Distribution Shift and Partial Data Coverage
Paper and Code
Oct 27, 2023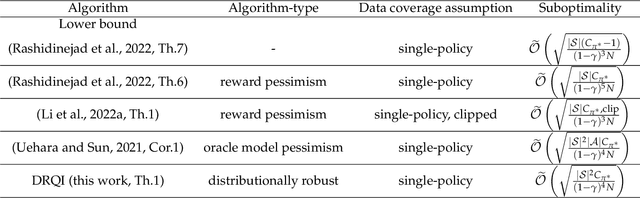
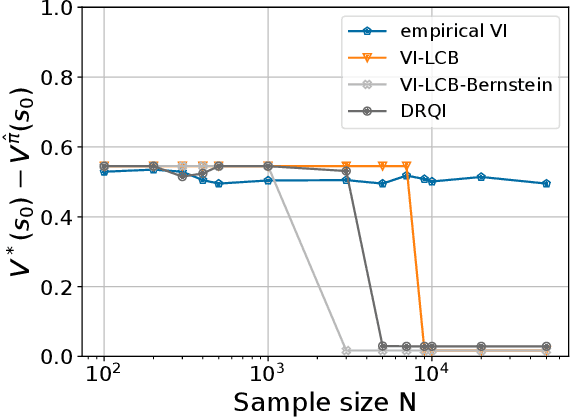

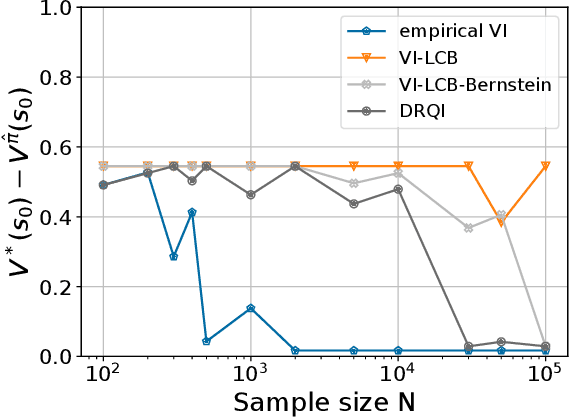
The goal of an offline reinforcement learning (RL) algorithm is to learn optimal polices using historical (offline) data, without access to the environment for online exploration. One of the main challenges in offline RL is the distribution shift which refers to the difference between the state-action visitation distribution of the data generating policy and the learning policy. Many recent works have used the idea of pessimism for developing offline RL algorithms and characterizing their sample complexity under a relatively weak assumption of single policy concentrability. Different from the offline RL literature, the area of distributionally robust learning (DRL) offers a principled framework that uses a minimax formulation to tackle model mismatch between training and testing environments. In this work, we aim to bridge these two areas by showing that the DRL approach can be used to tackle the distributional shift problem in offline RL. In particular, we propose two offline RL algorithms using the DRL framework, for the tabular and linear function approximation settings, and characterize their sample complexity under the single policy concentrability assumption. We also demonstrate the superior performance our proposed algorithm through simulation experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge