Communication Efficient Decentralization for Smoothed Online Convex Optimization

We study the multi-agent Smoothed Online Convex Optimization (SOCO) problem, where $N$ agents interact through a communication graph. In each round, each agent $i$ receives a strongly convex hitting cost function $f^i_t$ in an online fashion and selects an action $x^i_t \in \mathbb{R}^d$. The objective is to minimize the global cumulative cost, which includes the sum of individual hitting costs $f^i_t(x^i_t)$, a temporal "switching cost" for changing decisions, and a spatial "dissimilarity cost" that penalizes deviations in decisions among neighboring agents. We propose the first decentralized algorithm for multi-agent SOCO and prove its asymptotic optimality. Our approach allows each agent to operate using only local information from its immediate neighbors in the graph. For finite-time performance, we establish that the optimality gap in competitive ratio decreases with the time horizon $T$ and can be conveniently tuned based on the per-round computation available to each agent. Moreover, our results hold even when the communication graph changes arbitrarily and adaptively over time. Finally, we establish that the computational complexity per round depends only logarithmically on the number of agents and almost linearly on their degree within the graph, ensuring scalability for large-system implementations.

Best of Both Worlds: Stochastic and Adversarial Convex Function Chasing

Convex function chasing (CFC) is an online optimization problem in which during each round $t$, a player plays an action $x_t$ in response to a hitting cost $f_t(x_t)$ and an additional cost of $c(x_t,x_{t-1})$ for switching actions. We study the CFC problem in stochastic and adversarial environments, giving algorithms that achieve performance guarantees simultaneously in both settings. Specifically, we consider the squared $\ell_2$-norm switching costs and a broad class of quadratic hitting costs for which the sequence of minimizers either forms a martingale or is chosen adversarially. This is the first work that studies the CFC problem using a stochastic framework. We provide a characterization of the optimal stochastic online algorithm and, drawing a comparison between the stochastic and adversarial scenarios, we demonstrate that the adversarial-optimal algorithm exhibits suboptimal performance in the stochastic context. Motivated by this, we provide a best-of-both-worlds algorithm that obtains robust adversarial performance while simultaneously achieving near-optimal stochastic performance.

Multi-Model Federated Learning with Provable Guarantees

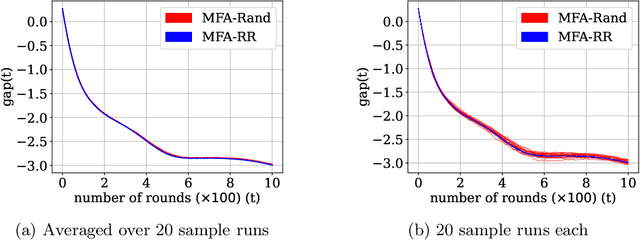
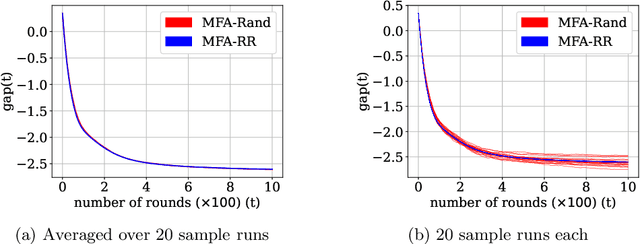
Federated Learning (FL) is a variant of distributed learning where edge devices collaborate to learn a model without sharing their data with the central server or each other. We refer to the process of training multiple independent models simultaneously in a federated setting using a common pool of clients as multi-model FL. In this work, we propose two variants of the popular FedAvg algorithm for multi-model FL, with provable convergence guarantees. We further show that for the same amount of computation, multi-model FL can have better performance than training each model separately. We supplement our theoretical results with experiments in strongly convex, convex, and non-convex settings.

Multi-Model Federated Learning

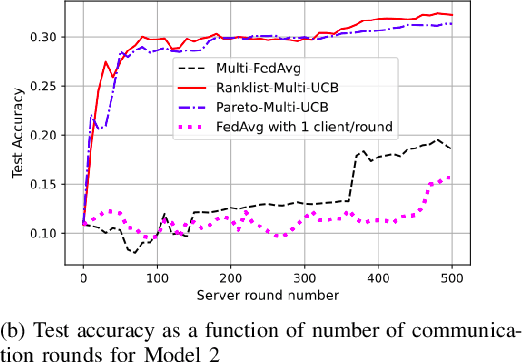
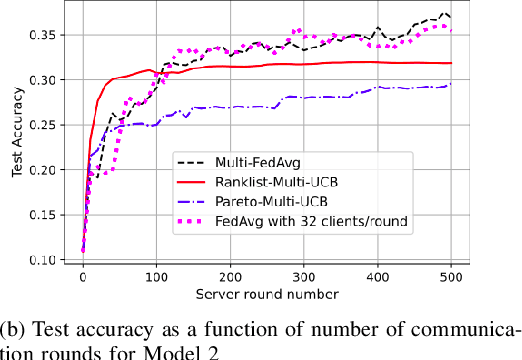
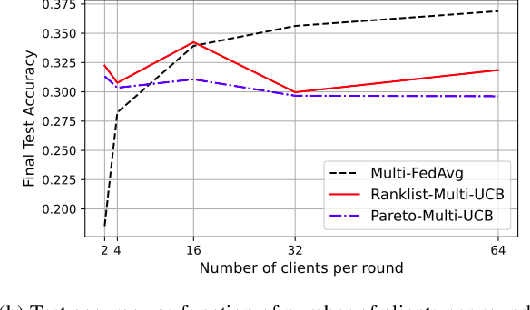
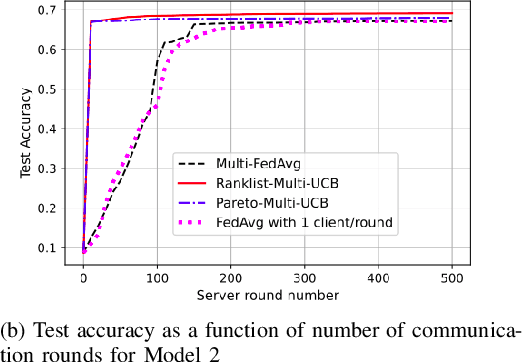
Federated learning is a form of distributed learning with the key challenge being the non-identically distributed nature of the data in the participating clients. In this paper, we extend federated learning to the setting where multiple unrelated models are trained simultaneously. Specifically, every client is able to train any one of M models at a time and the server maintains a model for each of the M models which is typically a suitably averaged version of the model computed by the clients. We propose multiple policies for assigning learning tasks to clients over time. In the first policy, we extend the widely studied FedAvg to multi-model learning by allotting models to clients in an i.i.d. stochastic manner. In addition, we propose two new policies for client selection in a multi-model federated setting which make decisions based on current local losses for each client-model pair. We compare the performance of the policies on tasks involving synthetic and real-world data and characterize the performance of the proposed policies. The key take-away from our work is that the proposed multi-model policies perform better or at least as good as single model training using FedAvg.