Sharayu Moharir
Cascading Bandits With Feedback
Nov 14, 2025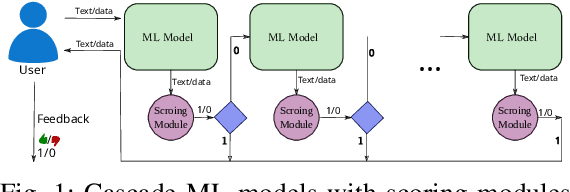
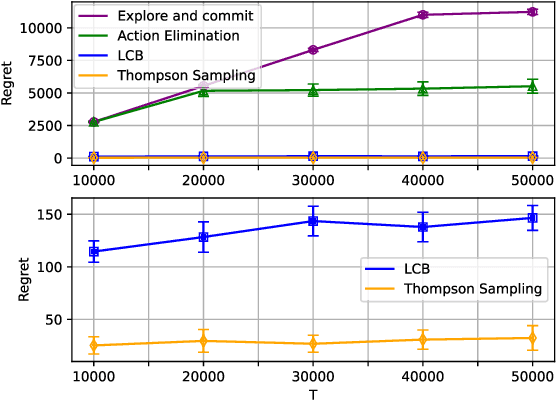
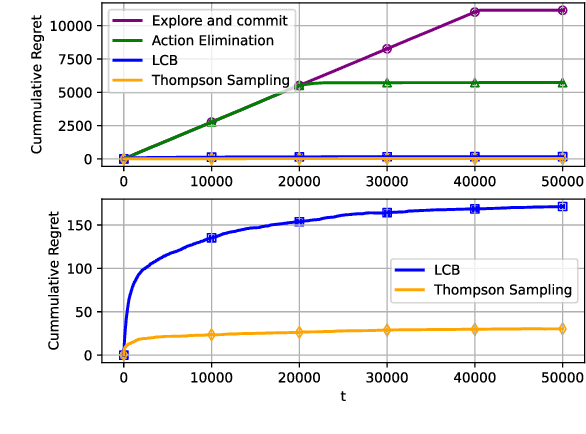
Abstract:Motivated by the challenges of edge inference, we study a variant of the cascade bandit model in which each arm corresponds to an inference model with an associated accuracy and error probability. We analyse four decision-making policies-Explore-then-Commit, Action Elimination, Lower Confidence Bound (LCB), and Thompson Sampling-and provide sharp theoretical regret guarantees for each. Unlike in classical bandit settings, Explore-then-Commit and Action Elimination incur suboptimal regret because they commit to a fixed ordering after the exploration phase, limiting their ability to adapt. In contrast, LCB and Thompson Sampling continuously update their decisions based on observed feedback, achieving constant O(1) regret. Simulations corroborate these theoretical findings, highlighting the crucial role of adaptivity for efficient edge inference under uncertainty.
Inference Offloading for Cost-Sensitive Binary Classification at the Edge
Sep 19, 2025Abstract:We focus on a binary classification problem in an edge intelligence system where false negatives are more costly than false positives. The system has a compact, locally deployed model, which is supplemented by a larger, remote model, which is accessible via the network by incurring an offloading cost. For each sample, our system first uses the locally deployed model for inference. Based on the output of the local model, the sample may be offloaded to the remote model. This work aims to understand the fundamental trade-off between classification accuracy and these offloading costs within such a hierarchical inference (HI) system. To optimize this system, we propose an online learning framework that continuously adapts a pair of thresholds on the local model's confidence scores. These thresholds determine the prediction of the local model and whether a sample is classified locally or offloaded to the remote model. We present a closed-form solution for the setting where the local model is calibrated. For the more general case of uncalibrated models, we introduce H2T2, an online two-threshold hierarchical inference policy, and prove it achieves sublinear regret. H2T2 is model-agnostic, requires no training, and learns in the inference phase using limited feedback. Simulations on real-world datasets show that H2T2 consistently outperforms naive and single-threshold HI policies, sometimes even surpassing offline optima. The policy also demonstrates robustness to distribution shifts and adapts effectively to mismatched classifiers.
Low-Regret and Low-Complexity Learning for Hierarchical Inference
Aug 12, 2025Abstract:This work focuses on Hierarchical Inference (HI) in edge intelligence systems, where a compact Local-ML model on an end-device works in conjunction with a high-accuracy Remote-ML model on an edge-server. HI aims to reduce latency, improve accuracy, and lower bandwidth usage by first using the Local-ML model for inference and offloading to the Remote-ML only when the local inference is likely incorrect. A critical challenge in HI is estimating the likelihood of the local inference being incorrect, especially when data distributions and offloading costs change over time -- a problem we term Hierarchical Inference Learning (HIL). We introduce a novel approach to HIL by modeling the probability of correct inference by the Local-ML as an increasing function of the model's confidence measure, a structure motivated by empirical observations but previously unexploited. We propose two policies, HI-LCB and HI-LCB-lite, based on the Upper Confidence Bound (UCB) framework. We demonstrate that both policies achieve order-optimal regret of $O(\log T)$, a significant improvement over existing HIL policies with $O(T^{2/3})$ regret guarantees. Notably, HI-LCB-lite has an $O(1)$ per-sample computational complexity, making it well-suited for deployment on devices with severe resource limitations. Simulations using real-world datasets confirm that our policies outperform existing state-of-the-art HIL methods.
Fixed-Confidence Best Arm Identification with Decreasing Variance
Feb 11, 2025Abstract:We focus on the problem of best-arm identification in a stochastic multi-arm bandit with temporally decreasing variances for the arms' rewards. We model arm rewards as Gaussian random variables with fixed means and variances that decrease with time. The cost incurred by the learner is modeled as a weighted sum of the time needed by the learner to identify the best arm, and the number of samples of arms collected by the learner before termination. Under this cost function, there is an incentive for the learner to not sample arms in all rounds, especially in the initial rounds. On the other hand, not sampling increases the termination time of the learner, which also increases cost. This trade-off necessitates new sampling strategies. We propose two policies. The first policy has an initial wait period with no sampling followed by continuous sampling. The second policy samples periodically and uses a weighted average of the rewards observed to identify the best arm. We provide analytical guarantees on the performance of both policies and supplement our theoretical results with simulations which show that our polices outperform the state-of-the-art policies for the classical best arm identification problem.
Constrained Best Arm Identification in Grouped Bandits
Dec 11, 2024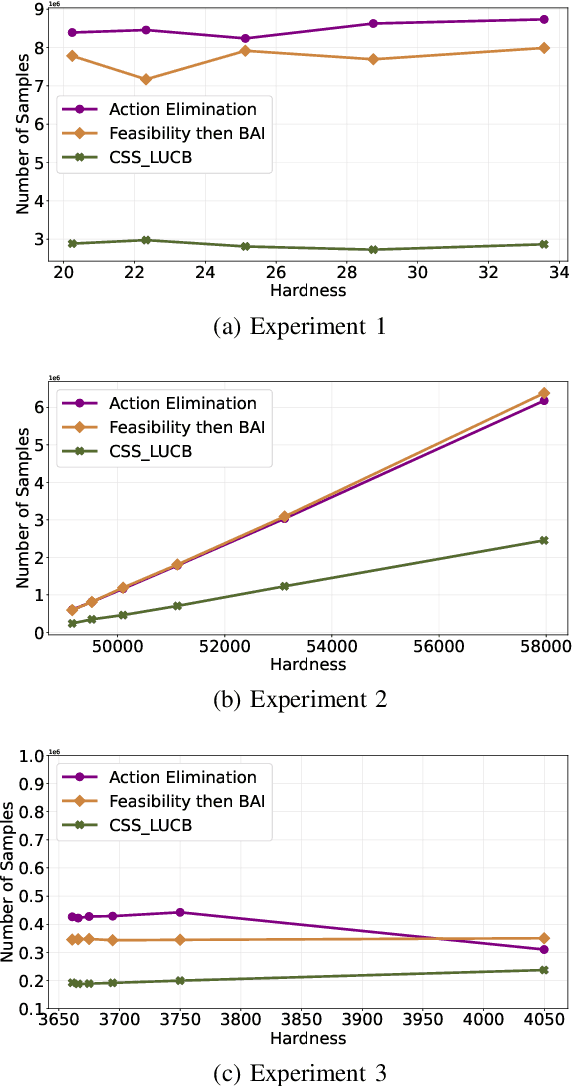
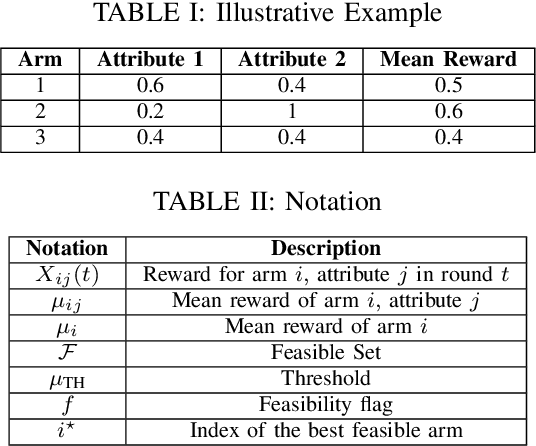
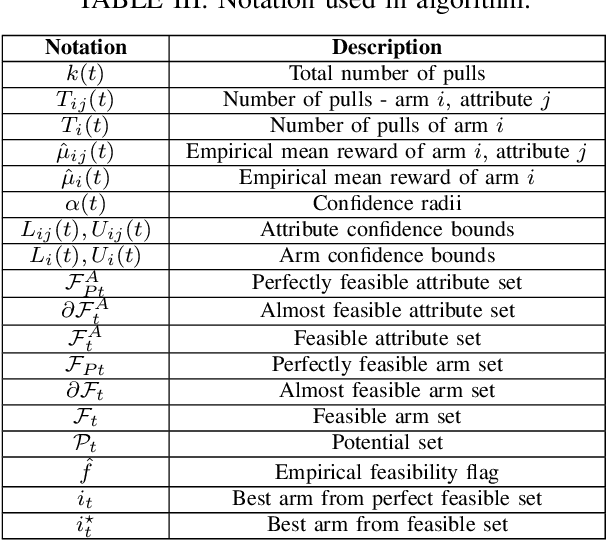
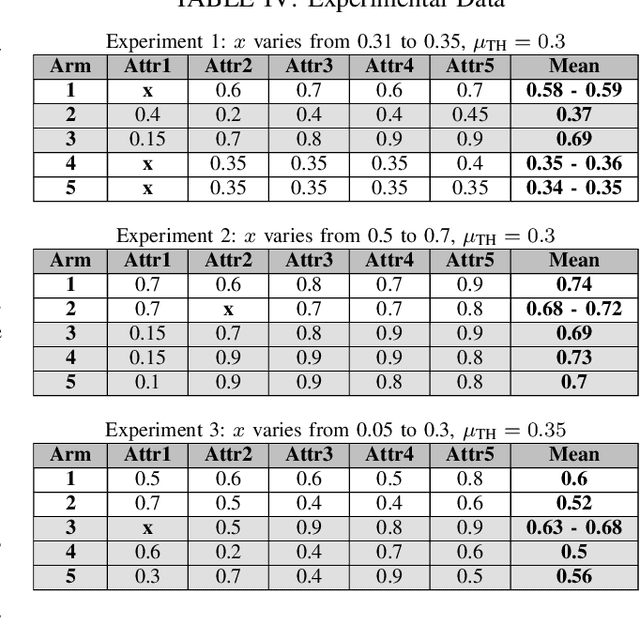
Abstract:We study a grouped bandit setting where each arm comprises multiple independent sub-arms referred to as attributes. Each attribute of each arm has an independent stochastic reward. We impose the constraint that for an arm to be deemed feasible, the mean reward of all its attributes should exceed a specified threshold. The goal is to find the arm with the highest mean reward averaged across attributes among the set of feasible arms in the fixed confidence setting. We first characterize a fundamental limit on the performance of any policy. Following this, we propose a near-optimal confidence interval-based policy to solve this problem and provide analytical guarantees for the policy. We compare the performance of the proposed policy with that of two suitably modified versions of action elimination via simulations.
Influencing Bandits: Arm Selection for Preference Shaping
Feb 29, 2024Abstract:We consider a non stationary multi-armed bandit in which the population preferences are positively and negatively reinforced by the observed rewards. The objective of the algorithm is to shape the population preferences to maximize the fraction of the population favouring a predetermined arm. For the case of binary opinions, two types of opinion dynamics are considered -- decreasing elasticity (modeled as a Polya urn with increasing number of balls) and constant elasticity (using the voter model). For the first case, we describe an Explore-then-commit policy and a Thompson sampling policy and analyse the regret for each of these policies. We then show that these algorithms and their analyses carry over to the constant elasticity case. We also describe a Thompson sampling based algorithm for the case when more than two types of opinions are present. Finally, we discuss the case where presence of multiple recommendation systems gives rise to a trade-off between their popularity and opinion shaping objectives.
On the Regret of Online Edge Service Hosting
Mar 13, 2023



Abstract:We consider the problem of service hosting where a service provider can dynamically rent edge resources via short term contracts to ensure better quality of service to its customers. The service can also be partially hosted at the edge, in which case, customers' requests can be partially served at the edge. The total cost incurred by the system is modeled as a combination of the rent cost, the service cost incurred due to latency in serving customers, and the fetch cost incurred as a result of the bandwidth used to fetch the code/databases of the service from the cloud servers to host the service at the edge. In this paper, we compare multiple hosting policies with regret as a metric, defined as the difference in the cost incurred by the policy and the optimal policy over some time horizon $T$. In particular we consider the Retro Renting (RR) and Follow The Perturbed Leader (FTPL) policies proposed in the literature and provide performance guarantees on the regret of these policies. We show that under i.i.d stochastic arrivals, RR policy has linear regret while FTPL policy has constant regret. Next, we propose a variant of FTPL, namely Wait then FTPL (W-FTPL), which also has constant regret while demonstrating much better dependence on the fetch cost. We also show that under adversarial arrivals, RR policy has linear regret while both FTPL and W-FTPL have regret $\mathrm{O}(\sqrt{T})$ which is order-optimal.
Multi-Model Federated Learning with Provable Guarantees
Jul 17, 2022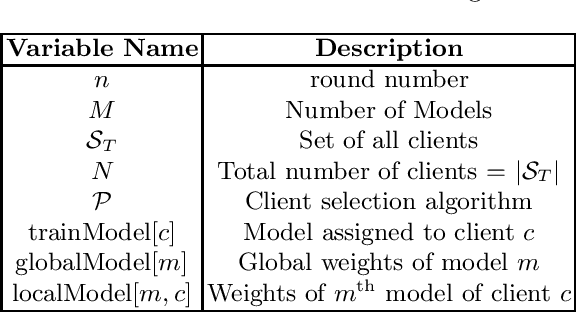
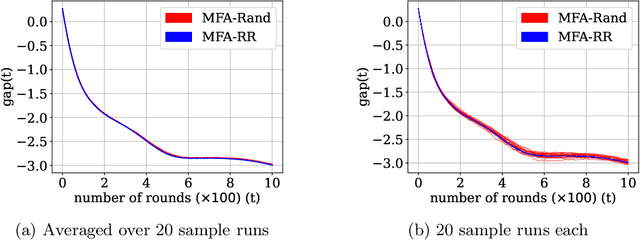

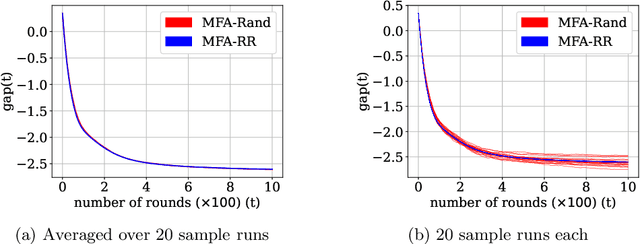
Abstract:Federated Learning (FL) is a variant of distributed learning where edge devices collaborate to learn a model without sharing their data with the central server or each other. We refer to the process of training multiple independent models simultaneously in a federated setting using a common pool of clients as multi-model FL. In this work, we propose two variants of the popular FedAvg algorithm for multi-model FL, with provable convergence guarantees. We further show that for the same amount of computation, multi-model FL can have better performance than training each model separately. We supplement our theoretical results with experiments in strongly convex, convex, and non-convex settings.
Multi-Model Federated Learning
Jan 07, 2022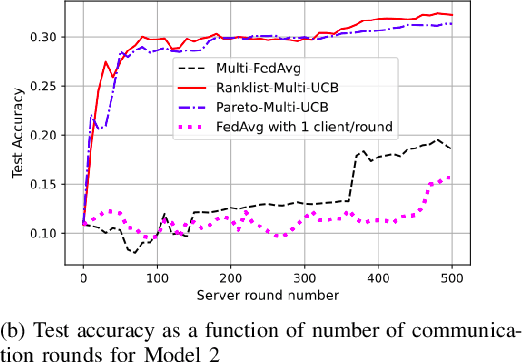
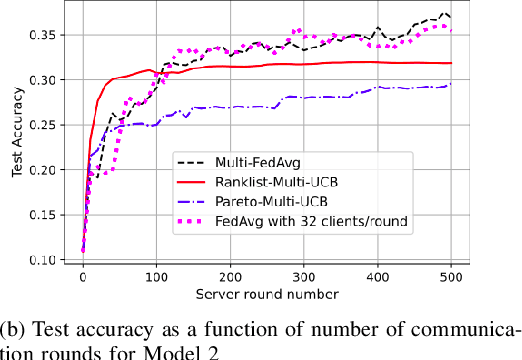
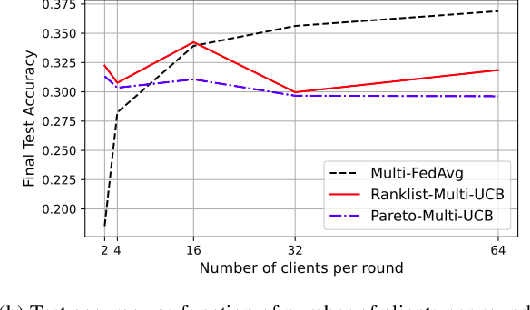
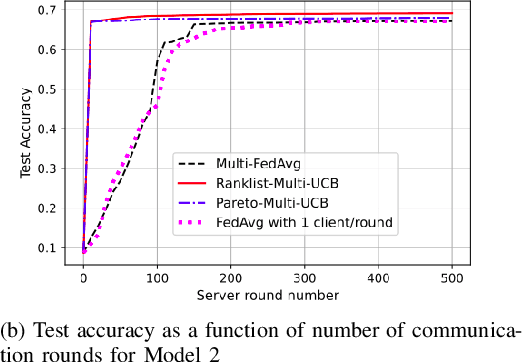
Abstract:Federated learning is a form of distributed learning with the key challenge being the non-identically distributed nature of the data in the participating clients. In this paper, we extend federated learning to the setting where multiple unrelated models are trained simultaneously. Specifically, every client is able to train any one of M models at a time and the server maintains a model for each of the M models which is typically a suitably averaged version of the model computed by the clients. We propose multiple policies for assigning learning tasks to clients over time. In the first policy, we extend the widely studied FedAvg to multi-model learning by allotting models to clients in an i.i.d. stochastic manner. In addition, we propose two new policies for client selection in a multi-model federated setting which make decisions based on current local losses for each client-model pair. We compare the performance of the policies on tasks involving synthetic and real-world data and characterize the performance of the proposed policies. The key take-away from our work is that the proposed multi-model policies perform better or at least as good as single model training using FedAvg.
Greedy $k$-Center from Noisy Distance Samples
Nov 03, 2020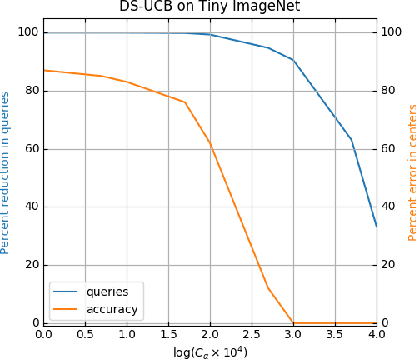
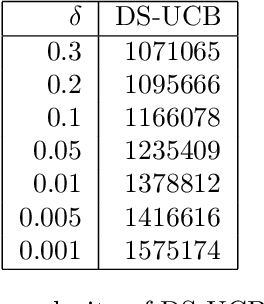
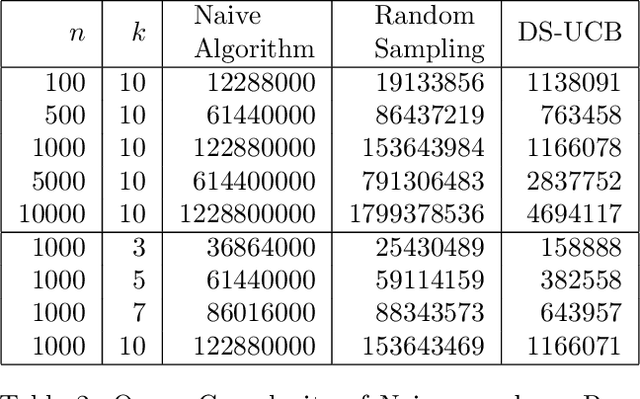

Abstract:We study a variant of the canonical $k$-center problem over a set of vertices in a metric space, where the underlying distances are apriori unknown. Instead, we can query an oracle which provides noisy/incomplete estimates of the distance between any pair of vertices. We consider two oracle models: Dimension Sampling where each query to the oracle returns the distance between a pair of points in one dimension; and Noisy Distance Sampling where the oracle returns the true distance corrupted by noise. We propose active algorithms, based on ideas such as UCB and Thompson sampling developed in the closely related Multi-Armed Bandit problem, which adaptively decide which queries to send to the oracle and are able to solve the $k$-center problem within an approximation ratio of two with high probability. We analytically characterize instance-dependent query complexity of our algorithms and also demonstrate significant improvements over naive implementations via numerical evaluations on two real-world datasets (Tiny ImageNet and UT Zappos50K).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge