Kota Srinivas Reddy
Sequential Spectral Clustering of Data Sequences
Sep 11, 2025Abstract:We study the problem of nonparametric clustering of data sequences, where each data sequence comprises i.i.d. samples generated from an unknown distribution. The true clusters are the clusters obtained using the Spectral clustering algorithm (SPEC) on the pairwise distance between the true distributions corresponding to the data sequences. Since the true distributions are unknown, the objective is to estimate the clusters by observing the minimum number of samples from the data sequences for a given error probability. To solve this problem, we propose the Sequential Spectral clustering algorithm (SEQ-SPEC), and show that it stops in finite time almost surely and is exponentially consistent. We also propose a computationally more efficient algorithm called the Incremental Approximate Sequential Spectral clustering algorithm (IA-SEQ-SPEC). Through simulations, we show that both our proposed algorithms perform better than the fixed sample size SPEC, the Sequential $K$-Medoids clustering algorithm (SEQ-KMED) and the Sequential Single Linkage clustering algorithm (SEQ-SLINK). The IA-SEQ-SPEC, while being computationally efficient, performs close to SEQ-SPEC on both synthetic and real-world datasets. To the best of our knowledge, this is the first work on spectral clustering of data sequences under a sequential framework.
Fixed-Confidence Best Arm Identification with Decreasing Variance
Feb 11, 2025Abstract:We focus on the problem of best-arm identification in a stochastic multi-arm bandit with temporally decreasing variances for the arms' rewards. We model arm rewards as Gaussian random variables with fixed means and variances that decrease with time. The cost incurred by the learner is modeled as a weighted sum of the time needed by the learner to identify the best arm, and the number of samples of arms collected by the learner before termination. Under this cost function, there is an incentive for the learner to not sample arms in all rounds, especially in the initial rounds. On the other hand, not sampling increases the termination time of the learner, which also increases cost. This trade-off necessitates new sampling strategies. We propose two policies. The first policy has an initial wait period with no sampling followed by continuous sampling. The second policy samples periodically and uses a weighted average of the rewards observed to identify the best arm. We provide analytical guarantees on the performance of both policies and supplement our theoretical results with simulations which show that our polices outperform the state-of-the-art policies for the classical best arm identification problem.
Best Arm Identification in Bandits with Limited Precision Sampling
May 10, 2023Abstract:We study best arm identification in a variant of the multi-armed bandit problem where the learner has limited precision in arm selection. The learner can only sample arms via certain exploration bundles, which we refer to as boxes. In particular, at each sampling epoch, the learner selects a box, which in turn causes an arm to get pulled as per a box-specific probability distribution. The pulled arm and its instantaneous reward are revealed to the learner, whose goal is to find the best arm by minimising the expected stopping time, subject to an upper bound on the error probability. We present an asymptotic lower bound on the expected stopping time, which holds as the error probability vanishes. We show that the optimal allocation suggested by the lower bound is, in general, non-unique and therefore challenging to track. We propose a modified tracking-based algorithm to handle non-unique optimal allocations, and demonstrate that it is asymptotically optimal. We also present non-asymptotic lower and upper bounds on the stopping time in the simpler setting when the arms accessible from one box do not overlap with those of others.
Almost Cost-Free Communication in Federated Best Arm Identification
Aug 19, 2022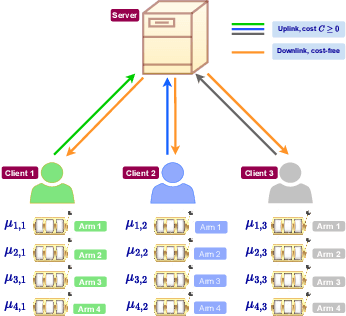

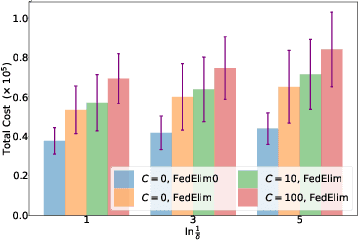
Abstract:We study the problem of best arm identification in a federated learning multi-armed bandit setup with a central server and multiple clients. Each client is associated with a multi-armed bandit in which each arm yields {\em i.i.d.}\ rewards following a Gaussian distribution with an unknown mean and known variance. The set of arms is assumed to be the same at all the clients. We define two notions of best arm -- local and global. The local best arm at a client is the arm with the largest mean among the arms local to the client, whereas the global best arm is the arm with the largest average mean across all the clients. We assume that each client can only observe the rewards from its local arms and thereby estimate its local best arm. The clients communicate with a central server on uplinks that entail a cost of $C\ge0$ units per usage per uplink. The global best arm is estimated at the server. The goal is to identify the local best arms and the global best arm with minimal total cost, defined as the sum of the total number of arm selections at all the clients and the total communication cost, subject to an upper bound on the error probability. We propose a novel algorithm {\sc FedElim} that is based on successive elimination and communicates only in exponential time steps and obtain a high probability instance-dependent upper bound on its total cost. The key takeaway from our paper is that for any $C\geq 0$ and error probabilities sufficiently small, the total number of arm selections (resp.\ the total cost) under {\sc FedElim} is at most~$2$ (resp.~$3$) times the maximum total number of arm selections under its variant that communicates in every time step. Additionally, we show that the latter is optimal in expectation up to a constant factor, thereby demonstrating that communication is almost cost-free in {\sc FedElim}. We numerically validate the efficacy of {\sc FedElim}.
Best Arm Identification in Restless Markov Multi-Armed Bandits
Mar 29, 2022Abstract:We study the problem of identifying the best arm in a multi-armed bandit environment when each arm is a time-homogeneous and ergodic discrete-time Markov process on a common, finite state space. The state evolution on each arm is governed by the arm's transition probability matrix (TPM). A decision entity that knows the set of arm TPMs but not the exact mapping of the TPMs to the arms, wishes to find the index of the best arm as quickly as possible, subject to an upper bound on the error probability. The decision entity selects one arm at a time sequentially, and all the unselected arms continue to undergo state evolution ({\em restless} arms). For this problem, we derive the first-known problem instance-dependent asymptotic lower bound on the growth rate of the expected time required to find the index of the best arm, where the asymptotics is as the error probability vanishes. Further, we propose a sequential policy that, for an input parameter $R$, forcibly selects an arm that has not been selected for $R$ consecutive time instants. We show that this policy achieves an upper bound that depends on $R$ and is monotonically non-increasing as $R\to\infty$. The question of whether, in general, the limiting value of the upper bound as $R\to\infty$ matches with the lower bound, remains open. We identify a special case in which the upper and the lower bounds match. Prior works on best arm identification have dealt with (a) independent and identically distributed observations from the arms, and (b) rested Markov arms, whereas our work deals with the more difficult setting of restless Markov arms.
Query complexity of heavy hitter estimation
May 29, 2020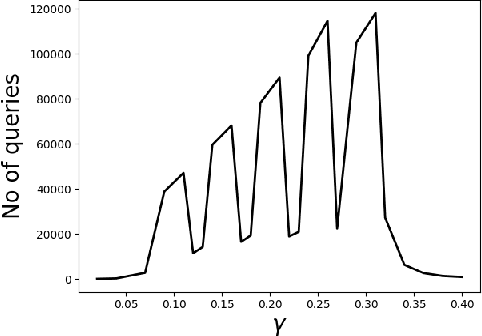

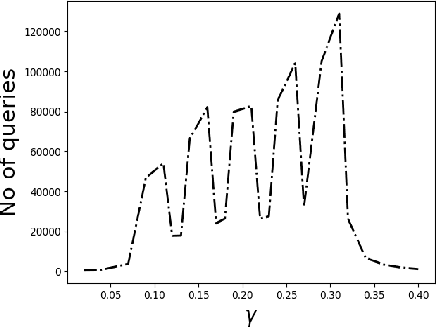
Abstract:We consider the problem of identifying the subset $\mathcal{S}^{\gamma}_{\mathcal{P}}$ of elements in the support of an underlying distribution $\mathcal{P}$ whose probability value is larger than a given threshold $\gamma$, by actively querying an oracle to gain information about a sequence $X_1, X_2, \ldots$ of $i.i.d.$ samples drawn from $\mathcal{P}$. We consider two query models: $(a)$ each query is an index $i$ and the oracle return the value $X_i$ and $(b)$ each query is a pair $(i,j)$ and the oracle gives a binary answer confirming if $X_i = X_j$ or not. For each of these query models, we design sequential estimation algorithms which at each round, either decide what query to send to the oracle depending on the entire history of responses or decide to stop and output an estimate of $\mathcal{S}^{\gamma}_{\mathcal{P}}$, which is required to be correct with some pre-specified large probability. We provide upper bounds on the query complexity of the algorithms for any distribution $\mathcal{P}$ and also derive lower bounds on the optimal query complexity under the two query models. We also consider noisy versions of the two query models and propose robust estimators which can effectively counter the noise in the oracle responses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge