Nikhil Karamchandani
Cascading Bandits With Feedback
Nov 14, 2025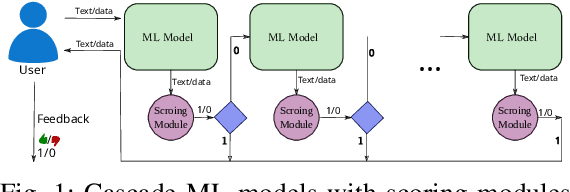
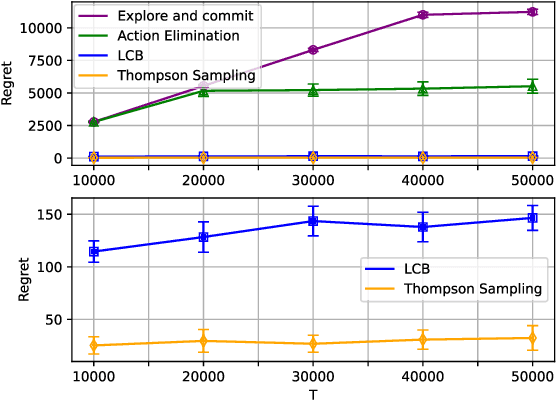
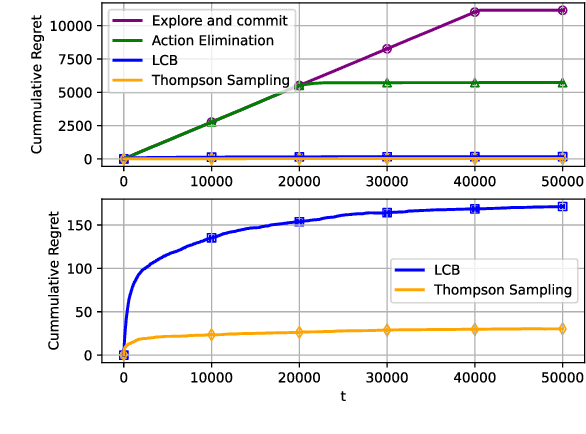
Abstract:Motivated by the challenges of edge inference, we study a variant of the cascade bandit model in which each arm corresponds to an inference model with an associated accuracy and error probability. We analyse four decision-making policies-Explore-then-Commit, Action Elimination, Lower Confidence Bound (LCB), and Thompson Sampling-and provide sharp theoretical regret guarantees for each. Unlike in classical bandit settings, Explore-then-Commit and Action Elimination incur suboptimal regret because they commit to a fixed ordering after the exploration phase, limiting their ability to adapt. In contrast, LCB and Thompson Sampling continuously update their decisions based on observed feedback, achieving constant O(1) regret. Simulations corroborate these theoretical findings, highlighting the crucial role of adaptivity for efficient edge inference under uncertainty.
Near Optimal Best Arm Identification for Clustered Bandits
May 15, 2025Abstract:This work investigates the problem of best arm identification for multi-agent multi-armed bandits. We consider $N$ agents grouped into $M$ clusters, where each cluster solves a stochastic bandit problem. The mapping between agents and bandits is a priori unknown. Each bandit is associated with $K$ arms, and the goal is to identify the best arm for each agent under a $\delta$-probably correct ($\delta$-PC) framework, while minimizing sample complexity and communication overhead. We propose two novel algorithms: Clustering then Best Arm Identification (Cl-BAI) and Best Arm Identification then Clustering (BAI-Cl). Cl-BAI uses a two-phase approach that first clusters agents based on the bandit problems they are learning, followed by identifying the best arm for each cluster. BAI-Cl reverses the sequence by identifying the best arms first and then clustering agents accordingly. Both algorithms leverage the successive elimination framework to ensure computational efficiency and high accuracy. We establish $\delta$-PC guarantees for both methods, derive bounds on their sample complexity, and provide a lower bound for this problem class. Moreover, when $M$ is small (a constant), we show that the sample complexity of a variant of BAI-Cl is minimax optimal in an order-wise sense. Experiments on synthetic and real-world datasets (MovieLens, Yelp) demonstrate the superior performance of the proposed algorithms in terms of sample and communication efficiency, particularly in settings where $M \ll N$.
Representative Arm Identification: A fixed confidence approach to identify cluster representatives
Aug 26, 2024
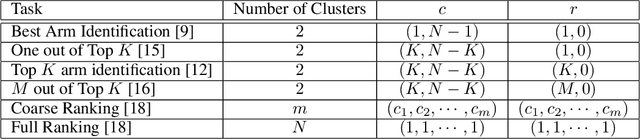
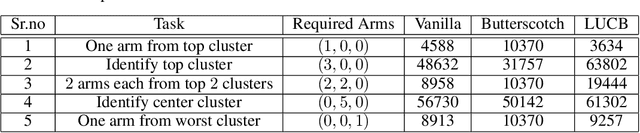
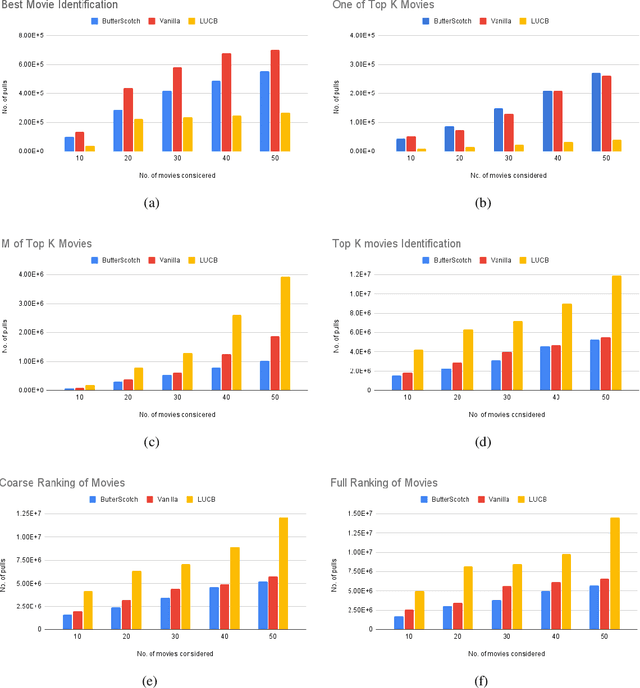
Abstract:We study the representative arm identification (RAI) problem in the multi-armed bandits (MAB) framework, wherein we have a collection of arms, each associated with an unknown reward distribution. An underlying instance is defined by a partitioning of the arms into clusters of predefined sizes, such that for any $j > i$, all arms in cluster $i$ have a larger mean reward than those in cluster $j$. The goal in RAI is to reliably identify a certain prespecified number of arms from each cluster, while using as few arm pulls as possible. The RAI problem covers as special cases several well-studied MAB problems such as identifying the best arm or any $M$ out of the top $K$, as well as both full and coarse ranking. We start by providing an instance-dependent lower bound on the sample complexity of any feasible algorithm for this setting. We then propose two algorithms, based on the idea of confidence intervals, and provide high probability upper bounds on their sample complexity, which orderwise match the lower bound. Finally, we do an empirical comparison of both algorithms along with an LUCB-type alternative on both synthetic and real-world datasets, and demonstrate the superior performance of our proposed schemes in most cases.
Best Arm Identification in Bandits with Limited Precision Sampling
May 10, 2023Abstract:We study best arm identification in a variant of the multi-armed bandit problem where the learner has limited precision in arm selection. The learner can only sample arms via certain exploration bundles, which we refer to as boxes. In particular, at each sampling epoch, the learner selects a box, which in turn causes an arm to get pulled as per a box-specific probability distribution. The pulled arm and its instantaneous reward are revealed to the learner, whose goal is to find the best arm by minimising the expected stopping time, subject to an upper bound on the error probability. We present an asymptotic lower bound on the expected stopping time, which holds as the error probability vanishes. We show that the optimal allocation suggested by the lower bound is, in general, non-unique and therefore challenging to track. We propose a modified tracking-based algorithm to handle non-unique optimal allocations, and demonstrate that it is asymptotically optimal. We also present non-asymptotic lower and upper bounds on the stopping time in the simpler setting when the arms accessible from one box do not overlap with those of others.
ICQ: A Quantization Scheme for Best-Arm Identification Over Bit-Constrained Channels
Apr 30, 2023



Abstract:We study the problem of best-arm identification in a distributed variant of the multi-armed bandit setting, with a central learner and multiple agents. Each agent is associated with an arm of the bandit, generating stochastic rewards following an unknown distribution. Further, each agent can communicate the observed rewards with the learner over a bit-constrained channel. We propose a novel quantization scheme called Inflating Confidence for Quantization (ICQ) that can be applied to existing confidence-bound based learning algorithms such as Successive Elimination. We analyze the performance of ICQ applied to Successive Elimination and show that the overall algorithm, named ICQ-SE, has the order-optimal sample complexity as that of the (unquantized) SE algorithm. Moreover, it requires only an exponentially sparse frequency of communication between the learner and the agents, thus requiring considerably fewer bits than existing quantization schemes to successfully identify the best arm. We validate the performance improvement offered by ICQ with other quantization methods through numerical experiments.
On the Regret of Online Edge Service Hosting
Mar 13, 2023



Abstract:We consider the problem of service hosting where a service provider can dynamically rent edge resources via short term contracts to ensure better quality of service to its customers. The service can also be partially hosted at the edge, in which case, customers' requests can be partially served at the edge. The total cost incurred by the system is modeled as a combination of the rent cost, the service cost incurred due to latency in serving customers, and the fetch cost incurred as a result of the bandwidth used to fetch the code/databases of the service from the cloud servers to host the service at the edge. In this paper, we compare multiple hosting policies with regret as a metric, defined as the difference in the cost incurred by the policy and the optimal policy over some time horizon $T$. In particular we consider the Retro Renting (RR) and Follow The Perturbed Leader (FTPL) policies proposed in the literature and provide performance guarantees on the regret of these policies. We show that under i.i.d stochastic arrivals, RR policy has linear regret while FTPL policy has constant regret. Next, we propose a variant of FTPL, namely Wait then FTPL (W-FTPL), which also has constant regret while demonstrating much better dependence on the fetch cost. We also show that under adversarial arrivals, RR policy has linear regret while both FTPL and W-FTPL have regret $\mathrm{O}(\sqrt{T})$ which is order-optimal.
Sequential Community Mode Estimation
Nov 16, 2021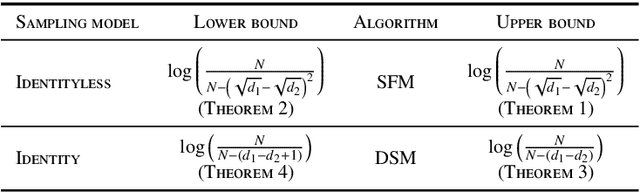
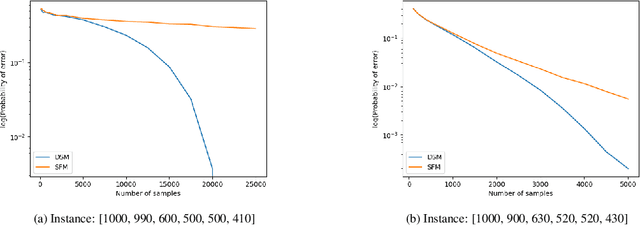

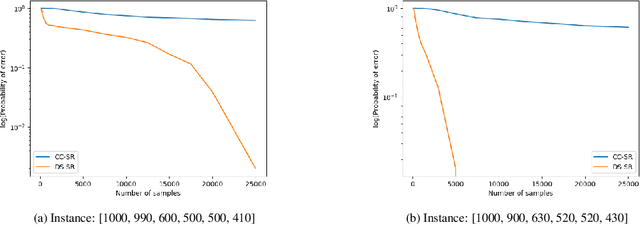
Abstract:We consider a population, partitioned into a set of communities, and study the problem of identifying the largest community within the population via sequential, random sampling of individuals. There are multiple sampling domains, referred to as \emph{boxes}, which also partition the population. Each box may consist of individuals of different communities, and each community may in turn be spread across multiple boxes. The learning agent can, at any time, sample (with replacement) a random individual from any chosen box; when this is done, the agent learns the community the sampled individual belongs to, and also whether or not this individual has been sampled before. The goal of the agent is to minimize the probability of mis-identifying the largest community in a \emph{fixed budget} setting, by optimizing both the sampling strategy as well as the decision rule. We propose and analyse novel algorithms for this problem, and also establish information theoretic lower bounds on the probability of error under any algorithm. In several cases of interest, the exponential decay rates of the probability of error under our algorithms are shown to be optimal up to constant factors. The proposed algorithms are further validated via simulations on real-world datasets.
Greedy $k$-Center from Noisy Distance Samples
Nov 03, 2020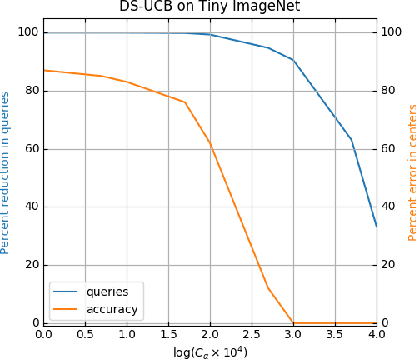
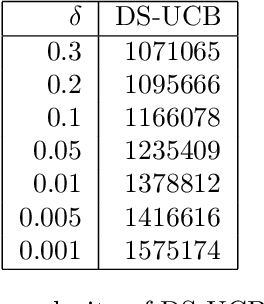
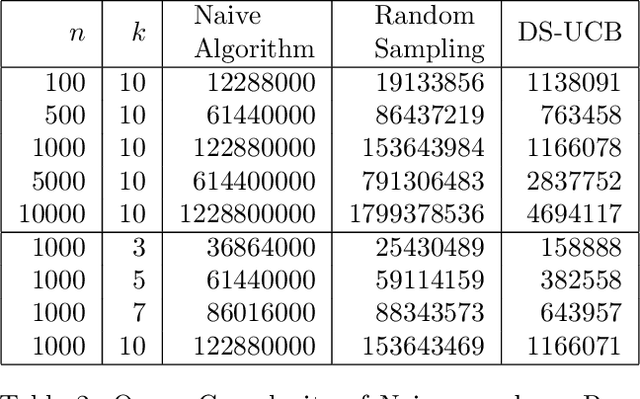

Abstract:We study a variant of the canonical $k$-center problem over a set of vertices in a metric space, where the underlying distances are apriori unknown. Instead, we can query an oracle which provides noisy/incomplete estimates of the distance between any pair of vertices. We consider two oracle models: Dimension Sampling where each query to the oracle returns the distance between a pair of points in one dimension; and Noisy Distance Sampling where the oracle returns the true distance corrupted by noise. We propose active algorithms, based on ideas such as UCB and Thompson sampling developed in the closely related Multi-Armed Bandit problem, which adaptively decide which queries to send to the oracle and are able to solve the $k$-center problem within an approximation ratio of two with high probability. We analytically characterize instance-dependent query complexity of our algorithms and also demonstrate significant improvements over naive implementations via numerical evaluations on two real-world datasets (Tiny ImageNet and UT Zappos50K).
Query Complexity of k-NN based Mode Estimation
Oct 26, 2020



Abstract:Motivated by the mode estimation problem of an unknown multivariate probability density function, we study the problem of identifying the point with the minimum k-th nearest neighbor distance for a given dataset of n points. We study the case where the pairwise distances are apriori unknown, but we have access to an oracle which we can query to get noisy information about the distance between any pair of points. For two natural oracle models, we design a sequential learning algorithm, based on the idea of confidence intervals, which adaptively decides which queries to send to the oracle and is able to correctly solve the problem with high probability. We derive instance-dependent upper bounds on the query complexity of our proposed scheme and also demonstrate significant improvement over the performance of other baselines via extensive numerical evaluations.
Query complexity of heavy hitter estimation
May 29, 2020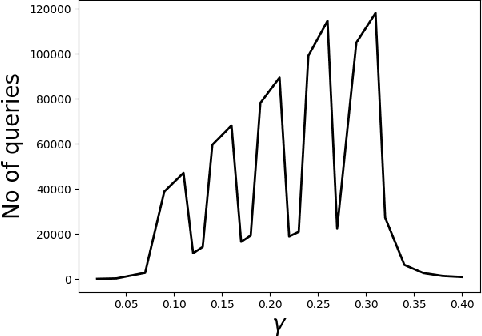
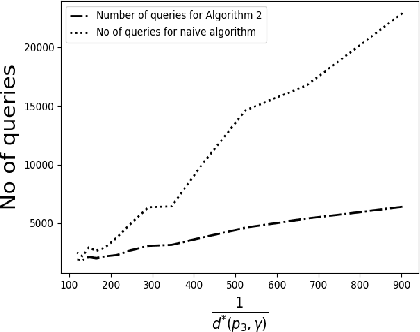
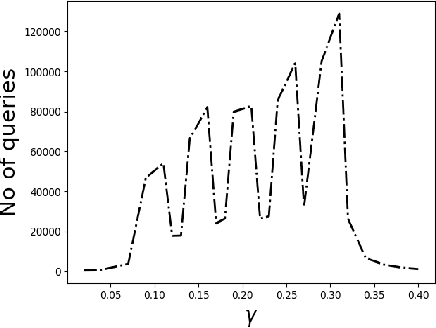
Abstract:We consider the problem of identifying the subset $\mathcal{S}^{\gamma}_{\mathcal{P}}$ of elements in the support of an underlying distribution $\mathcal{P}$ whose probability value is larger than a given threshold $\gamma$, by actively querying an oracle to gain information about a sequence $X_1, X_2, \ldots$ of $i.i.d.$ samples drawn from $\mathcal{P}$. We consider two query models: $(a)$ each query is an index $i$ and the oracle return the value $X_i$ and $(b)$ each query is a pair $(i,j)$ and the oracle gives a binary answer confirming if $X_i = X_j$ or not. For each of these query models, we design sequential estimation algorithms which at each round, either decide what query to send to the oracle depending on the entire history of responses or decide to stop and output an estimate of $\mathcal{S}^{\gamma}_{\mathcal{P}}$, which is required to be correct with some pre-specified large probability. We provide upper bounds on the query complexity of the algorithms for any distribution $\mathcal{P}$ and also derive lower bounds on the optimal query complexity under the two query models. We also consider noisy versions of the two query models and propose robust estimators which can effectively counter the noise in the oracle responses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge