Sequential Community Mode Estimation

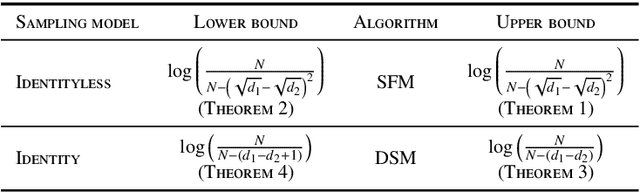
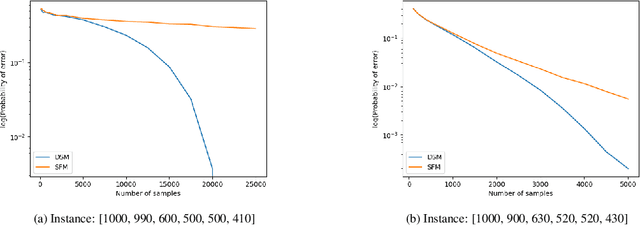
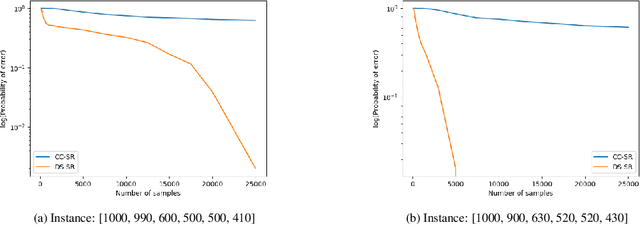
We consider a population, partitioned into a set of communities, and study the problem of identifying the largest community within the population via sequential, random sampling of individuals. There are multiple sampling domains, referred to as \emph{boxes}, which also partition the population. Each box may consist of individuals of different communities, and each community may in turn be spread across multiple boxes. The learning agent can, at any time, sample (with replacement) a random individual from any chosen box; when this is done, the agent learns the community the sampled individual belongs to, and also whether or not this individual has been sampled before. The goal of the agent is to minimize the probability of mis-identifying the largest community in a \emph{fixed budget} setting, by optimizing both the sampling strategy as well as the decision rule. We propose and analyse novel algorithms for this problem, and also establish information theoretic lower bounds on the probability of error under any algorithm. In several cases of interest, the exponential decay rates of the probability of error under our algorithms are shown to be optimal up to constant factors. The proposed algorithms are further validated via simulations on real-world datasets.

PAC Mode Estimation using PPR Martingale Confidence Sequences

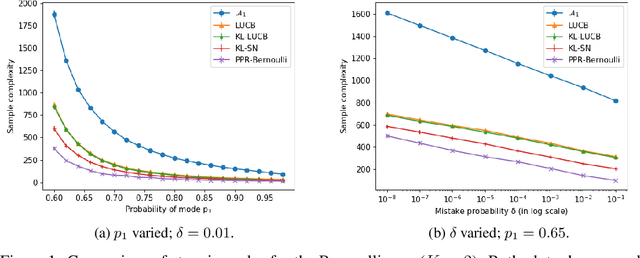
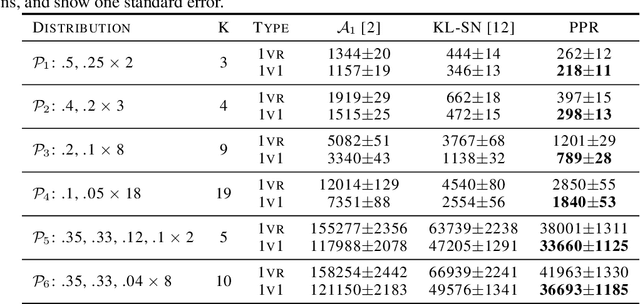
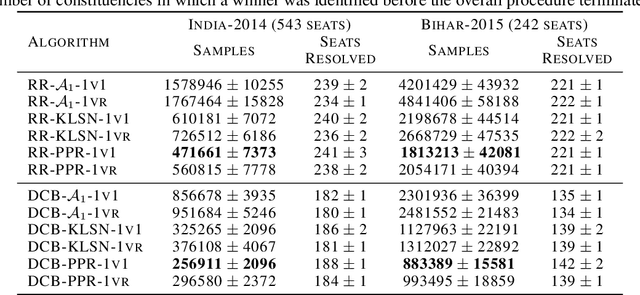
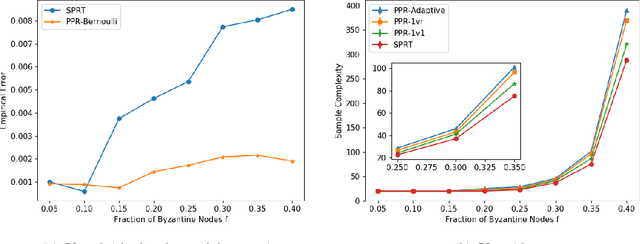
We consider the problem of correctly identifying the mode of a discrete distribution $\mathcal{P}$ with sufficiently high probability by observing a sequence of i.i.d. samples drawn according to $\mathcal{P}$. This problem reduces to the estimation of a single parameter when $\mathcal{P}$ has a support set of size $K = 2$. Noting the efficiency of prior-posterior-ratio (PPR) martingale confidence sequences for handling this special case, we propose a generalisation to mode estimation, in which $\mathcal{P}$ may take $K \geq 2$ values. We observe that the "one-versus-one" principle yields a more efficient generalisation than the "one-versus-rest" alternative. Our resulting stopping rule, denoted PPR-ME, is optimal in its sample complexity up to a logarithmic factor. Moreover, PPR-ME empirically outperforms several other competing approaches for mode estimation. We demonstrate the gains offered by PPR-ME in two practical applications: (1) sample-based forecasting of the winner in indirect election systems, and (2) efficient verification of smart contracts in permissionless blockchains.