PAC Mode Estimation using PPR Martingale Confidence Sequences
Paper and Code
Sep 10, 2021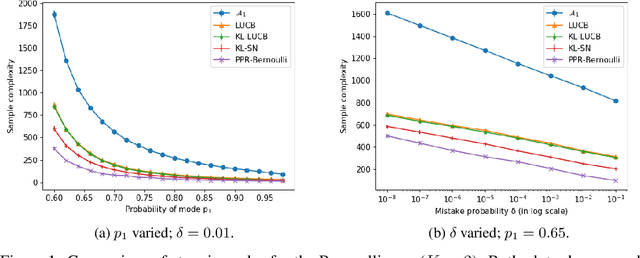
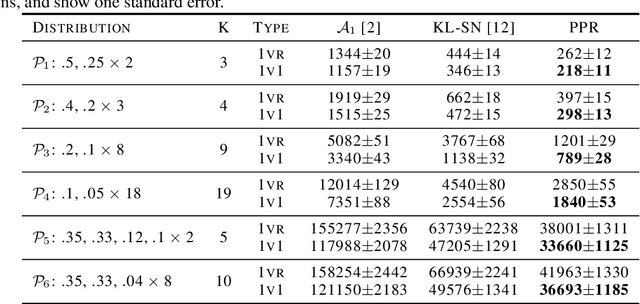
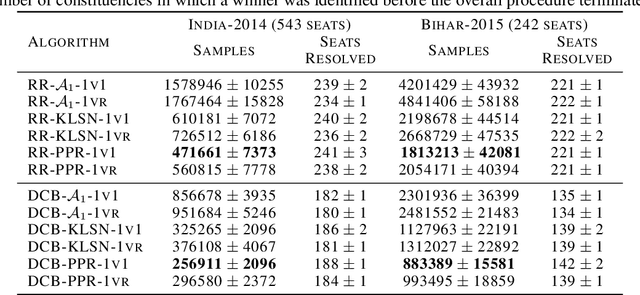
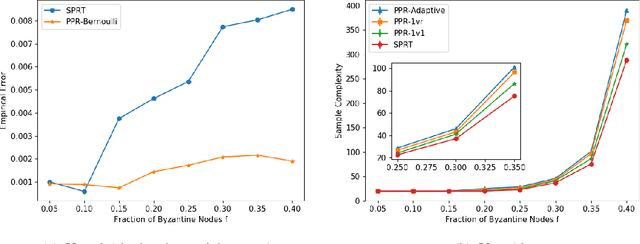
We consider the problem of correctly identifying the mode of a discrete distribution $\mathcal{P}$ with sufficiently high probability by observing a sequence of i.i.d. samples drawn according to $\mathcal{P}$. This problem reduces to the estimation of a single parameter when $\mathcal{P}$ has a support set of size $K = 2$. Noting the efficiency of prior-posterior-ratio (PPR) martingale confidence sequences for handling this special case, we propose a generalisation to mode estimation, in which $\mathcal{P}$ may take $K \geq 2$ values. We observe that the "one-versus-one" principle yields a more efficient generalisation than the "one-versus-rest" alternative. Our resulting stopping rule, denoted PPR-ME, is optimal in its sample complexity up to a logarithmic factor. Moreover, PPR-ME empirically outperforms several other competing approaches for mode estimation. We demonstrate the gains offered by PPR-ME in two practical applications: (1) sample-based forecasting of the winner in indirect election systems, and (2) efficient verification of smart contracts in permissionless blockchains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge