Efficient Computation of Blackwell Optimal Policies using Rational Functions

Markov Decision Problems (MDPs) provide a foundational framework for modelling sequential decision-making across diverse domains, guided by optimality criteria such as discounted and average rewards. However, these criteria have inherent limitations: discounted optimality may overly prioritise short-term rewards, while average optimality relies on strong structural assumptions. Blackwell optimality addresses these challenges, offering a robust and comprehensive criterion that ensures optimality under both discounted and average reward frameworks. Despite its theoretical appeal, existing algorithms for computing Blackwell Optimal (BO) policies are computationally expensive or hard to implement. In this paper we describe procedures for computing BO policies using an ordering of rational functions in the vicinity of $1$. We adapt state-of-the-art algorithms for deterministic and general MDPs, replacing numerical evaluations with symbolic operations on rational functions to derive bounds independent of bit complexity. For deterministic MDPs, we give the first strongly polynomial-time algorithms for computing BO policies, and for general MDPs we obtain the first subexponential-time algorithm. We further generalise several policy iteration algorithms, extending the best known upper bounds from the discounted to the Blackwell criterion.

Howard's Policy Iteration is Subexponential for Deterministic Markov Decision Problems with Rewards of Fixed Bit-size and Arbitrary Discount Factor

Howard's Policy Iteration (HPI) is a classic algorithm for solving Markov Decision Problems (MDPs). HPI uses a "greedy" switching rule to update from any non-optimal policy to a dominating one, iterating until an optimal policy is found. Despite its introduction over 60 years ago, the best-known upper bounds on HPI's running time remain exponential in the number of states -- indeed even on the restricted class of MDPs with only deterministic transitions (DMDPs). Meanwhile, the tightest lower bound for HPI for MDPs with a constant number of actions per state is only linear. In this paper, we report a significant improvement: a subexponential upper bound for HPI on DMDPs, which is parameterised by the bit-size of the rewards, while independent of the discount factor. The same upper bound also applies to DMDPs with only two possible rewards (which may be of arbitrary size).

A New Interpretation of the Certainty-Equivalence Approach for PAC Reinforcement Learning with a Generative Model

Reinforcement learning (RL) enables an agent interacting with an unknown MDP $M$ to optimise its behaviour by observing transitions sampled from $M$. A natural entity that emerges in the agent's reasoning is $\widehat{M}$, the maximum likelihood estimate of $M$ based on the observed transitions. The well-known \textit{certainty-equivalence} method (CEM) dictates that the agent update its behaviour to $\widehat{\pi}$, which is an optimal policy for $\widehat{M}$. Not only is CEM intuitive, it has been shown to enjoy minimax-optimal sample complexity in some regions of the parameter space for PAC RL with a generative model~\citep{Agarwal2020GenModel}. A seemingly unrelated algorithm is the ``trajectory tree method'' (TTM)~\citep{Kearns+MN:1999}, originally developed for efficient decision-time planning in large POMDPs. This paper presents a theoretical investigation that stems from the surprising finding that CEM may indeed be viewed as an application of TTM. The qualitative benefits of this view are (1) new and simple proofs of sample complexity upper bounds for CEM, in fact under a (2) weaker assumption on the rewards than is prevalent in the current literature. Our analysis applies to both non-stationary and stationary MDPs. Quantitatively, we obtain (3) improvements in the sample-complexity upper bounds for CEM both for non-stationary and stationary MDPs, in the regime that the ``mistake probability'' $\delta$ is small. Additionally, we show (4) a lower bound on the sample complexity for finite-horizon MDPs, which establishes the minimax-optimality of our upper bound for non-stationary MDPs in the small-$\delta$ regime.

Artificial Intelligence and Life in 2030: The One Hundred Year Study on Artificial Intelligence

In September 2016, Stanford's "One Hundred Year Study on Artificial Intelligence" project (AI100) issued the first report of its planned long-term periodic assessment of artificial intelligence (AI) and its impact on society. It was written by a panel of 17 study authors, each of whom is deeply rooted in AI research, chaired by Peter Stone of the University of Texas at Austin. The report, entitled "Artificial Intelligence and Life in 2030," examines eight domains of typical urban settings on which AI is likely to have impact over the coming years: transportation, home and service robots, healthcare, education, public safety and security, low-resource communities, employment and workplace, and entertainment. It aims to provide the general public with a scientifically and technologically accurate portrayal of the current state of AI and its potential and to help guide decisions in industry and governments, as well as to inform research and development in the field. The charge for this report was given to the panel by the AI100 Standing Committee, chaired by Barbara Grosz of Harvard University.

PAC Mode Estimation using PPR Martingale Confidence Sequences

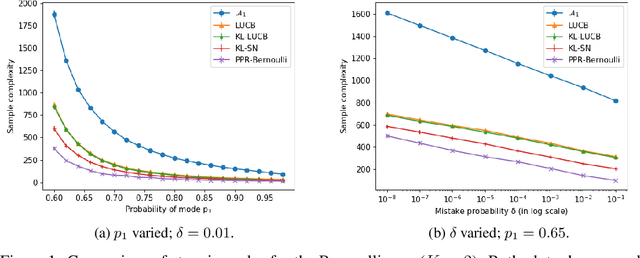
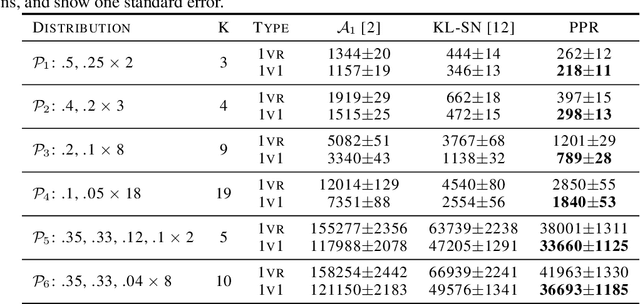
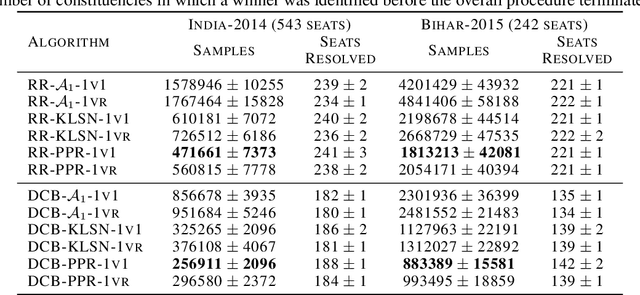
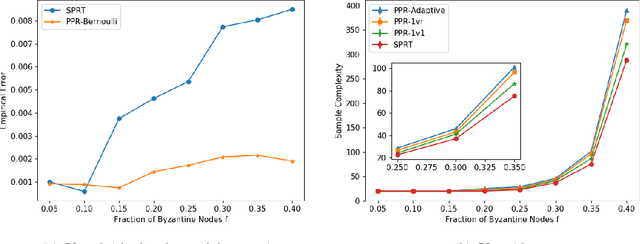
We consider the problem of correctly identifying the mode of a discrete distribution $\mathcal{P}$ with sufficiently high probability by observing a sequence of i.i.d. samples drawn according to $\mathcal{P}$. This problem reduces to the estimation of a single parameter when $\mathcal{P}$ has a support set of size $K = 2$. Noting the efficiency of prior-posterior-ratio (PPR) martingale confidence sequences for handling this special case, we propose a generalisation to mode estimation, in which $\mathcal{P}$ may take $K \geq 2$ values. We observe that the "one-versus-one" principle yields a more efficient generalisation than the "one-versus-rest" alternative. Our resulting stopping rule, denoted PPR-ME, is optimal in its sample complexity up to a logarithmic factor. Moreover, PPR-ME empirically outperforms several other competing approaches for mode estimation. We demonstrate the gains offered by PPR-ME in two practical applications: (1) sample-based forecasting of the winner in indirect election systems, and (2) efficient verification of smart contracts in permissionless blockchains.

An Analysis of Frame-skipping in Reinforcement Learning

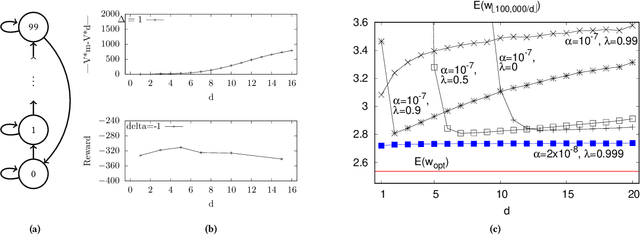
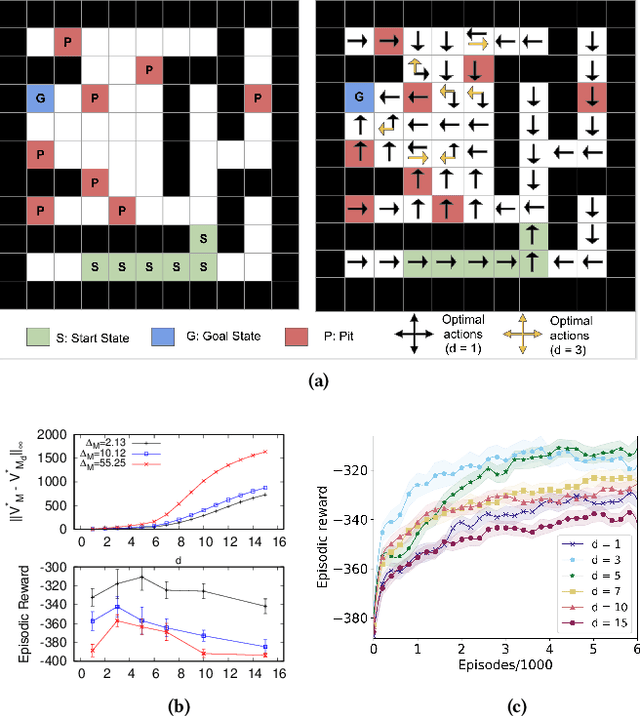
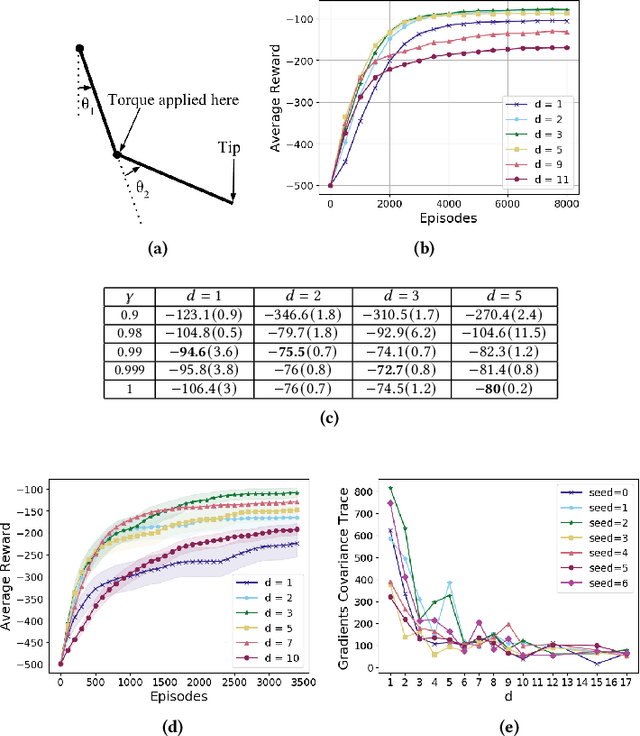
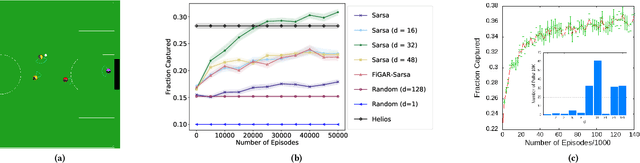
In the practice of sequential decision making, agents are often designed to sense state at regular intervals of $d$ time steps, $d > 1$, ignoring state information in between sensing steps. While it is clear that this practice can reduce sensing and compute costs, recent results indicate a further benefit. On many Atari console games, reinforcement learning (RL) algorithms deliver substantially better policies when run with $d > 1$ -- in fact with $d$ even as high as $180$. In this paper, we investigate the role of the parameter $d$ in RL; $d$ is called the "frame-skip" parameter, since states in the Atari domain are images. For evaluating a fixed policy, we observe that under standard conditions, frame-skipping does not affect asymptotic consistency. Depending on other parameters, it can possibly even benefit learning. To use $d > 1$ in the control setting, one must first specify which $d$-step open-loop action sequences can be executed in between sensing steps. We focus on "action-repetition", the common restriction of this choice to $d$-length sequences of the same action. We define a task-dependent quantity called the "price of inertia", in terms of which we upper-bound the loss incurred by action-repetition. We show that this loss may be offset by the gain brought to learning by a smaller task horizon. Our analysis is supported by experiments on different tasks and learning algorithms.

Lower Bounds for Policy Iteration on Multi-action MDPs

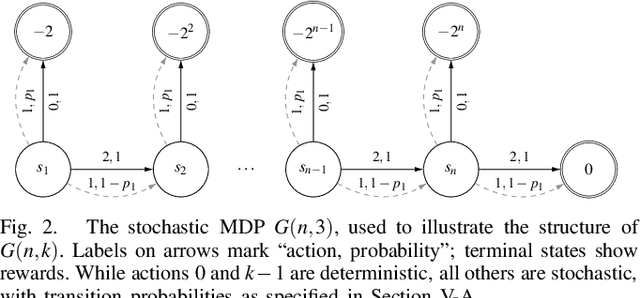
Policy Iteration (PI) is a classical family of algorithms to compute an optimal policy for any given Markov Decision Problem (MDP). The basic idea in PI is to begin with some initial policy and to repeatedly update the policy to one from an improving set, until an optimal policy is reached. Different variants of PI result from the (switching) rule used for improvement. An important theoretical question is how many iterations a specified PI variant will take to terminate as a function of the number of states $n$ and the number of actions $k$ in the input MDP. While there has been considerable progress towards upper-bounding this number, there are fewer results on lower bounds. In particular, existing lower bounds primarily focus on the special case of $k = 2$ actions. We devise lower bounds for $k \geq 3$. Our main result is that a particular variant of PI can take $\Omega(k^{n/2})$ iterations to terminate. We also generalise existing constructions on $2$-action MDPs to scale lower bounds by a factor of $k$ for some common deterministic variants of PI, and by $\log(k)$ for corresponding randomised variants.

Regret Minimisation in Multi-Armed Bandits Using Bounded Arm Memory

In this paper, we propose a constant word (RAM model) algorithm for regret minimisation for both finite and infinite Stochastic Multi-Armed Bandit (MAB) instances. Most of the existing regret minimisation algorithms need to remember the statistics of all the arms they encounter. This may become a problem for the cases where the number of available words of memory is limited. Designing an efficient regret minimisation algorithm that uses a constant number of words has long been interesting to the community. Some early attempts consider the number of arms to be infinite, and require the reward distribution of the arms to belong to some particular family. Recently, for finitely many-armed bandits an explore-then-commit based algorithm~\citep{Liau+PSY:2018} seems to escape such assumption. However, due to the underlying PAC-based elimination their method incurs a high regret. We present a conceptually simple, and efficient algorithm that needs to remember statistics of at most $M$ arms, and for any $K$-armed finite bandit instance it enjoys a $O(KM +K^{1.5}\sqrt{T\log (T/MK)}/M)$ upper-bound on regret. We extend it to achieve sub-linear \textit{quantile-regret}~\citep{RoyChaudhuri+K:2018} and empirically verify the efficiency of our algorithm via experiments.

PAC Identification of Many Good Arms in Stochastic Multi-Armed Bandits

We consider the problem of identifying any $k$ out of the best $m$ arms in an $n$-armed stochastic multi-armed bandit. Framed in the PAC setting, this particular problem generalises both the problem of `best subset selection' and that of selecting `one out of the best m' arms [arcsk 2017]. In applications such as crowd-sourcing and drug-designing, identifying a single good solution is often not sufficient. Moreover, finding the best subset might be hard due to the presence of many indistinguishably close solutions. Our generalisation of identifying exactly $k$ arms out of the best $m$, where $1 \leq k \leq m$, serves as a more effective alternative. We present a lower bound on the worst-case sample complexity for general $k$, and a fully sequential PAC algorithm, \GLUCB, which is more sample-efficient on easy instances. Also, extending our analysis to infinite-armed bandits, we present a PAC algorithm that is independent of $n$, which identifies an arm from the best $\rho$ fraction of arms using at most an additive poly-log number of samples than compared to the lower bound, thereby improving over [arcsk 2017] and [Aziz+AKA:2018]. The problem of identifying $k > 1$ distinct arms from the best $\rho$ fraction is not always well-defined; for a special class of this problem, we present lower and upper bounds. Finally, through a reduction, we establish a relation between upper bounds for the `one out of the best $\rho$' problem for infinite instances and the `one out of the best $m$' problem for finite instances. We conjecture that it is more efficient to solve `small' finite instances using the latter formulation, rather than going through the former.