New Insights into Channel vs Subspace Codes for Large-Scale Beamspace MIMO Channel Sensing

This paper provides novel insights into channel and subspace codes in nonadaptive channel sensing with a single RF chain. Observing that this problem naturally maps to a noncoherent decoding problem, we show that the sensing performance of the maximum likelihood (ML) angle estimator, which does not require knowledge of the typically unknown channel coefficient, is governed by two key terms: the minimum subspace distance and beam gain of the used beamformers. We derive an exact expression for the subspace distance of binary linear channel codes mapped to BPSK, which illuminates the relationship between subspace and Hamming distance, used to design subspace and channel codes, respectively. Our result also reveals why good Hamming distance alone is insufficient for sensing, and shows that well-known families of channel codes such as Reed-Muller codes, yield zero subspace distance and thereby poor sensing performance when used naively without proper codebook pruning. Finally, we introduce so-called beamspace subspace codes based on sparse antenna selection patterns (Golomb rulers), which we show provide near-optimal subspace distance. We demonstrate that this property of judiciously designed sparse arrays can be leveraged together with beamforming gain via convolutional beamspaces, enabling hardware- and sample-efficient channel sensing with theoretical guarantees in large-scale multiantenna communications.

Lower Bounds for Policy Iteration on Multi-action MDPs

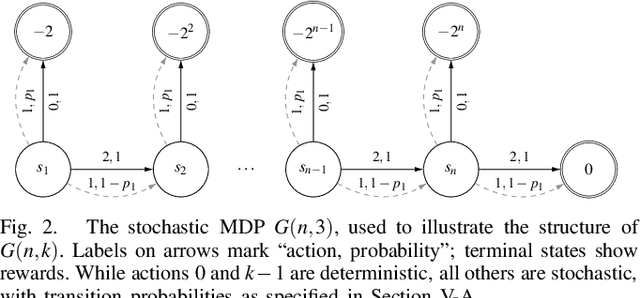
Policy Iteration (PI) is a classical family of algorithms to compute an optimal policy for any given Markov Decision Problem (MDP). The basic idea in PI is to begin with some initial policy and to repeatedly update the policy to one from an improving set, until an optimal policy is reached. Different variants of PI result from the (switching) rule used for improvement. An important theoretical question is how many iterations a specified PI variant will take to terminate as a function of the number of states $n$ and the number of actions $k$ in the input MDP. While there has been considerable progress towards upper-bounding this number, there are fewer results on lower bounds. In particular, existing lower bounds primarily focus on the special case of $k = 2$ actions. We devise lower bounds for $k \geq 3$. Our main result is that a particular variant of PI can take $\Omega(k^{n/2})$ iterations to terminate. We also generalise existing constructions on $2$-action MDPs to scale lower bounds by a factor of $k$ for some common deterministic variants of PI, and by $\log(k)$ for corresponding randomised variants.

Analysis of Lower Bounds for Simple Policy Iteration

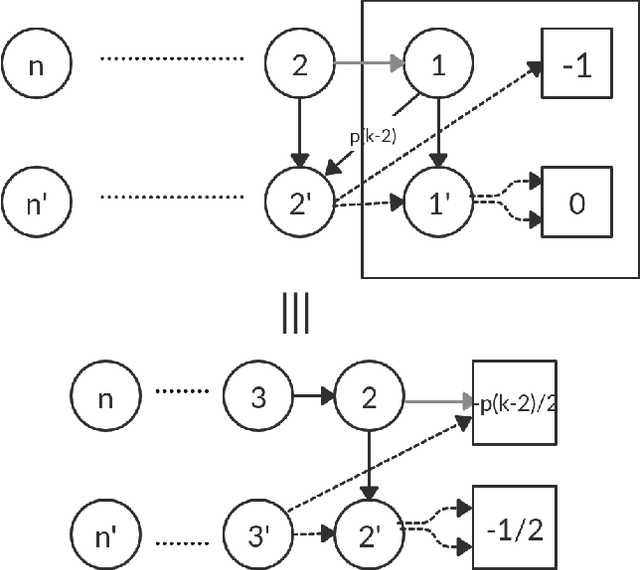
Policy iteration is a family of algorithms that are used to find an optimal policy for a given Markov Decision Problem (MDP). Simple Policy iteration (SPI) is a type of policy iteration where the strategy is to change the policy at exactly one improvable state at every step. Melekopoglou and Condon [1990] showed an exponential lower bound on the number of iterations taken by SPI for a 2 action MDP. The results have not been generalized to $k-$action MDP since. In this paper, we revisit the algorithm and the analysis done by Melekopoglou and Condon. We generalize the previous result and prove a novel exponential lower bound on the number of iterations taken by policy iteration for $N-$state, $k-$action MDPs. We construct a family of MDPs and give an index-based switching rule that yields a strong lower bound of $\mathcal{O}\big((3+k)2^{N/2-3}\big)$.