Invalid Logic, Equivalent Gains: The Bizarreness of Reasoning in Language Model Prompting

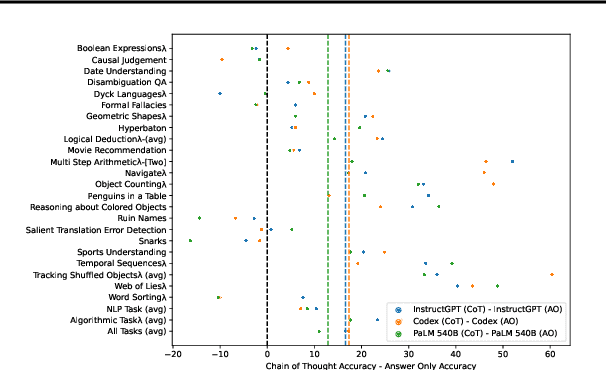
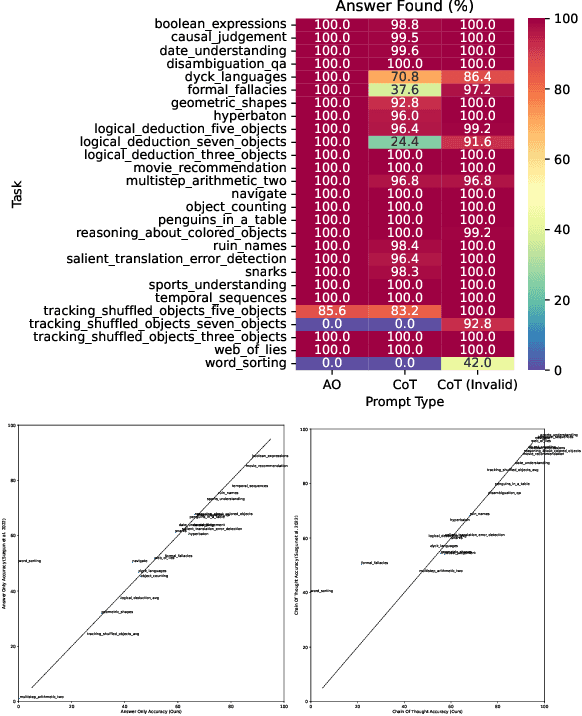
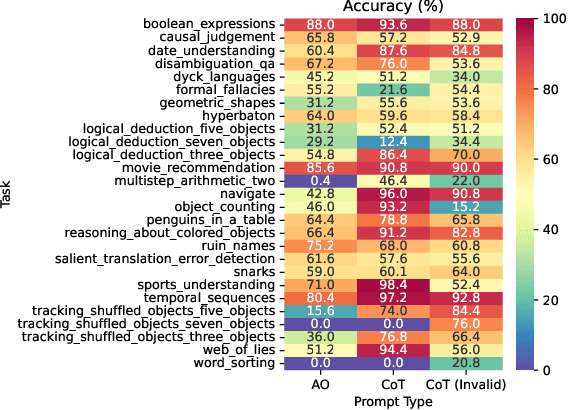
Language models can be prompted to reason through problems in a manner that significantly improves performance. However, \textit{why} such prompting improves performance is unclear. Recent work showed that using logically \textit{invalid} Chain-of-Thought (CoT) prompting improves performance almost as much as logically \textit{valid} CoT prompting, and that editing CoT prompts to replace problem-specific information with abstract information or out-of-distribution information typically doesn't harm performance. Critics have responded that these findings are based on too few and too easily solved tasks to draw meaningful conclusions. To resolve this dispute, we test whether logically invalid CoT prompts offer the same level of performance gains as logically valid prompts on the hardest tasks in the BIG-Bench benchmark, termed BIG-Bench Hard (BBH). We find that the logically \textit{invalid} reasoning prompts do indeed achieve similar performance gains on BBH tasks as logically valid reasoning prompts. We also discover that some CoT prompts used by previous works contain logical errors. This suggests that covariates beyond logically valid reasoning are responsible for performance improvements.

Lower Bounds for Policy Iteration on Multi-action MDPs

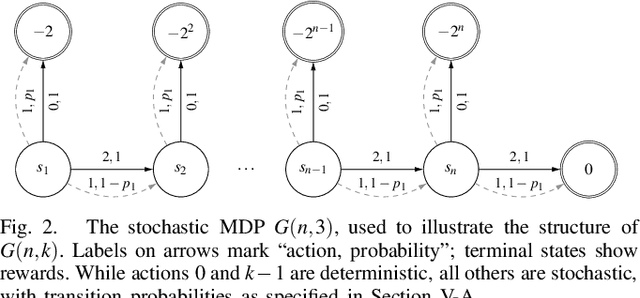
Policy Iteration (PI) is a classical family of algorithms to compute an optimal policy for any given Markov Decision Problem (MDP). The basic idea in PI is to begin with some initial policy and to repeatedly update the policy to one from an improving set, until an optimal policy is reached. Different variants of PI result from the (switching) rule used for improvement. An important theoretical question is how many iterations a specified PI variant will take to terminate as a function of the number of states $n$ and the number of actions $k$ in the input MDP. While there has been considerable progress towards upper-bounding this number, there are fewer results on lower bounds. In particular, existing lower bounds primarily focus on the special case of $k = 2$ actions. We devise lower bounds for $k \geq 3$. Our main result is that a particular variant of PI can take $\Omega(k^{n/2})$ iterations to terminate. We also generalise existing constructions on $2$-action MDPs to scale lower bounds by a factor of $k$ for some common deterministic variants of PI, and by $\log(k)$ for corresponding randomised variants.

Analysis of Lower Bounds for Simple Policy Iteration

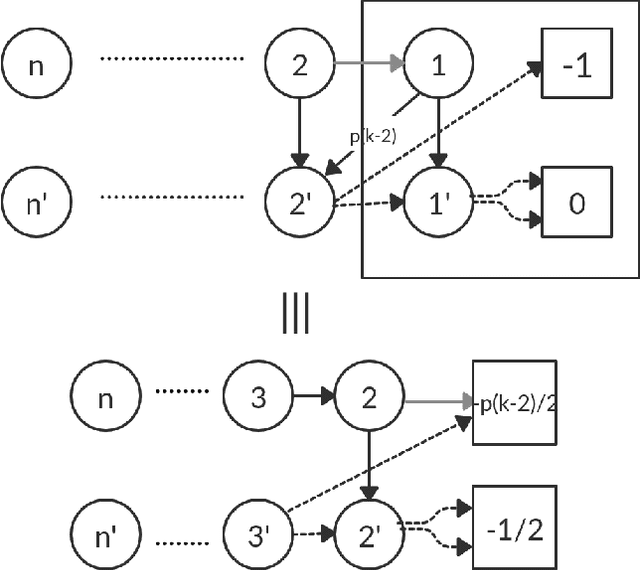
Policy iteration is a family of algorithms that are used to find an optimal policy for a given Markov Decision Problem (MDP). Simple Policy iteration (SPI) is a type of policy iteration where the strategy is to change the policy at exactly one improvable state at every step. Melekopoglou and Condon [1990] showed an exponential lower bound on the number of iterations taken by SPI for a 2 action MDP. The results have not been generalized to $k-$action MDP since. In this paper, we revisit the algorithm and the analysis done by Melekopoglou and Condon. We generalize the previous result and prove a novel exponential lower bound on the number of iterations taken by policy iteration for $N-$state, $k-$action MDPs. We construct a family of MDPs and give an index-based switching rule that yields a strong lower bound of $\mathcal{O}\big((3+k)2^{N/2-3}\big)$.