BioDiscoveryAgent: An AI Agent for Designing Genetic Perturbation Experiments

Agents based on large language models have shown great potential in accelerating scientific discovery by leveraging their rich background knowledge and reasoning capabilities. Here, we develop BioDiscoveryAgent, an agent that designs new experiments, reasons about their outcomes, and efficiently navigates the hypothesis space to reach desired solutions. We demonstrate our agent on the problem of designing genetic perturbation experiments, where the aim is to find a small subset out of many possible genes that, when perturbed, result in a specific phenotype (e.g., cell growth). Utilizing its biological knowledge, BioDiscoveryAgent can uniquely design new experiments without the need to train a machine learning model or explicitly design an acquisition function. Moreover, BioDiscoveryAgent achieves an average of 18% improvement in detecting desired phenotypes across five datasets, compared to existing Bayesian optimization baselines specifically trained for this task. Our evaluation includes one dataset that is unpublished, ensuring it is not part of the language model's training data. Additionally, BioDiscoveryAgent predicts gene combinations to perturb twice as accurately as a random baseline, a task so far not explored in the context of closed-loop experiment design. The agent also has access to tools for searching the biomedical literature, executing code to analyze biological datasets, and prompting another agent to critically evaluate its predictions. Overall, BioDiscoveryAgent is interpretable at every stage, representing an accessible new paradigm in the computational design of biological experiments with the potential to augment scientists' capabilities.

Benchmarking Large Language Models As AI Research Agents

Scientific experimentation involves an iterative process of creating hypotheses, designing experiments, running experiments, and analyzing the results. Can we build AI research agents to perform these long-horizon tasks? To take a step towards building and evaluating research agents on such open-ended decision-making tasks, we focus on the problem of machine learning engineering: given a task description and a dataset, build a high-performing model. In this paper, we propose MLAgentBench, a suite of ML tasks for benchmarking AI research agents. Agents can perform actions like reading/writing files, executing code, and inspecting outputs. With these actions, agents could run experiments, analyze the results, and modify the code of entire machine learning pipelines, such as data processing, architecture, training processes, etc. The benchmark then automatically evaluates the agent's performance objectively over various metrics related to performance and efficiency. We also design an LLM-based research agent to automatically perform experimentation loops in such an environment. Empirically, we find that a GPT-4-based research agent can feasibly build compelling ML models over many tasks in MLAgentBench, displaying highly interpretable plans and actions. However, the success rates vary considerably; they span from almost 90\% on well-established older datasets to as low as 10\% on recent Kaggle Challenges -- unavailable during the LLM model's pretraining -- and even 0\% on newer research challenges like BabyLM. Finally, we identify several key challenges for LLM-based research agents such as long-term planning and hallucination. Our code is released at https://github.com/snap-stanford/MLAgentBench.

Scoring Black-Box Models for Adversarial Robustness

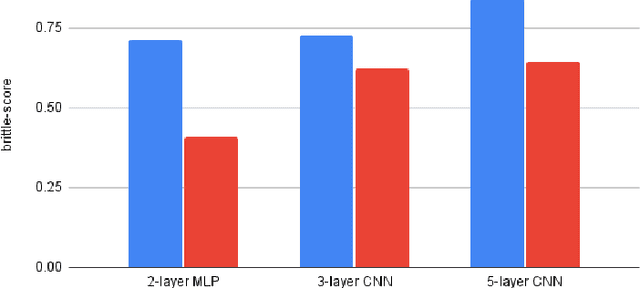
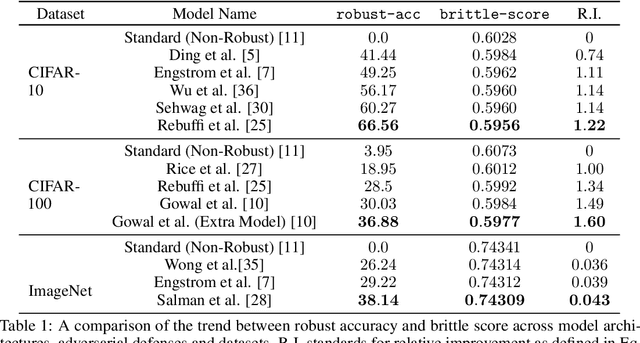
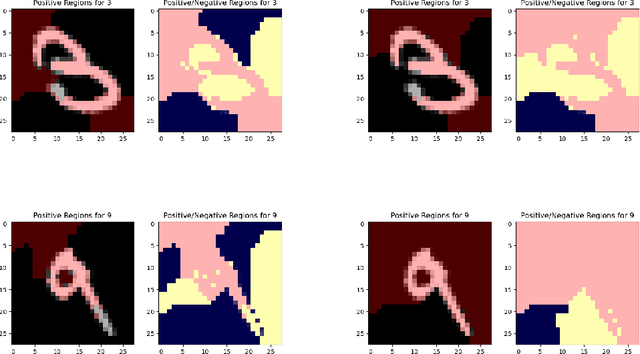
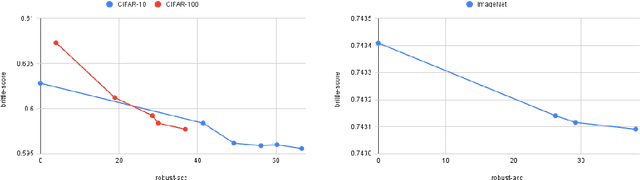
Deep neural networks are susceptible to adversarial inputs and various methods have been proposed to defend these models against adversarial attacks under different perturbation models. The robustness of models to adversarial attacks has been analyzed by first constructing adversarial inputs for the model, and then testing the model performance on the constructed adversarial inputs. Most of these attacks require the model to be white-box, need access to data labels, and finding adversarial inputs can be computationally expensive. We propose a simple scoring method for black-box models which indicates their robustness to adversarial input. We show that adversarially more robust models have a smaller $l_1$-norm of LIME weights and sharper explanations.

PAC Mode Estimation using PPR Martingale Confidence Sequences

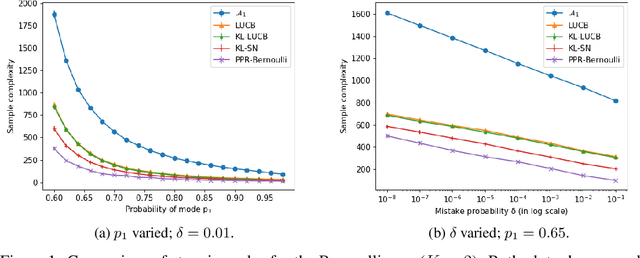
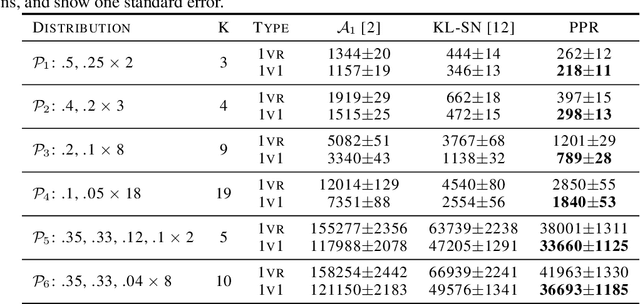
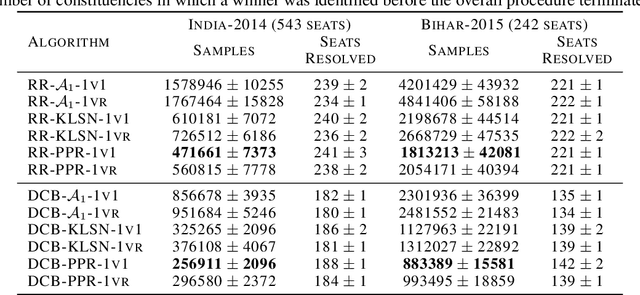
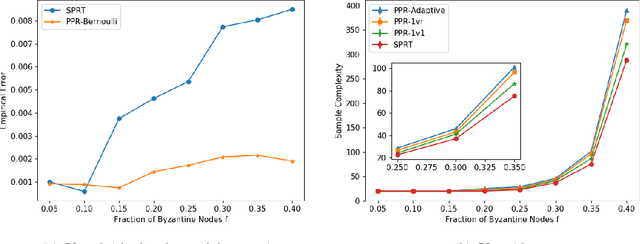
We consider the problem of correctly identifying the mode of a discrete distribution $\mathcal{P}$ with sufficiently high probability by observing a sequence of i.i.d. samples drawn according to $\mathcal{P}$. This problem reduces to the estimation of a single parameter when $\mathcal{P}$ has a support set of size $K = 2$. Noting the efficiency of prior-posterior-ratio (PPR) martingale confidence sequences for handling this special case, we propose a generalisation to mode estimation, in which $\mathcal{P}$ may take $K \geq 2$ values. We observe that the "one-versus-one" principle yields a more efficient generalisation than the "one-versus-rest" alternative. Our resulting stopping rule, denoted PPR-ME, is optimal in its sample complexity up to a logarithmic factor. Moreover, PPR-ME empirically outperforms several other competing approaches for mode estimation. We demonstrate the gains offered by PPR-ME in two practical applications: (1) sample-based forecasting of the winner in indirect election systems, and (2) efficient verification of smart contracts in permissionless blockchains.

Recovery of Joint Probability Distribution from one-way marginals: Low rank Tensors and Random Projections

Joint probability mass function (PMF) estimation is a fundamental machine learning problem. The number of free parameters scales exponentially with respect to the number of random variables. Hence, most work on nonparametric PMF estimation is based on some structural assumptions such as clique factorization adopted by probabilistic graphical models, imposition of low rank on the joint probability tensor and reconstruction from 3-way or 2-way marginals, etc. In the present work, we link random projections of data to the problem of PMF estimation using ideas from tomography. We integrate this idea with the idea of low-rank tensor decomposition to show that we can estimate the joint density from just one-way marginals in a transformed space. We provide a novel algorithm for recovering factors of the tensor from one-way marginals, test it across a variety of synthetic and real-world datasets, and also perform MAP inference on the estimated model for classification.

Stochastic Approximation Algorithms for Principal Component Analysis

Principal Component Analysis is a novel way of of dimensionality reduction. This problem essentially boils down to finding the top k eigen vectors of the data covariance matrix. A considerable amount of literature is found on algorithms meant to do so such as an online method be Warmuth and Kuzmin, Matrix Stochastic Gradient by Arora, Oja's method and many others. In this paper we see some of these stochastic approaches to the PCA optimization problem and comment on their convergence and runtime to obtain an epsilon sub-optimal solution. We revisit convex relaxation based methods for stochastic optimization of principal component analysis. While methods that directly solve the non convex problem have been shown to be optimal in terms of statistical and computational efficiency, the methods based on convex relaxation have been shown to enjoy comparable, or even superior, empirical performance. This motivates the need for a deeper formal understanding of the latter.