Karthik S. Gurumoorthy
Two-Dimensional Unknown View Tomography from Unknown Angle Distributions
Jan 06, 2025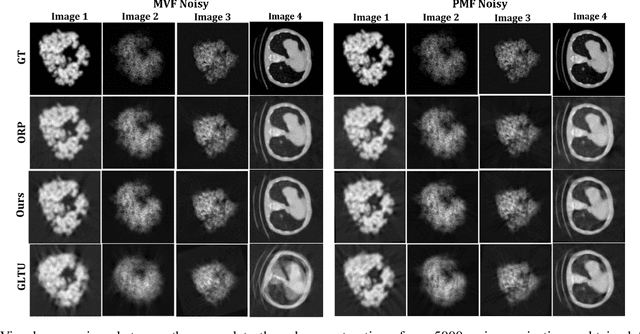
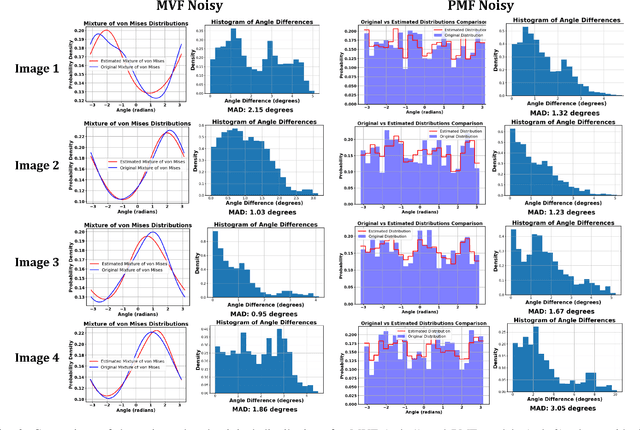


Abstract:This study presents a technique for 2D tomography under unknown viewing angles when the distribution of the viewing angles is also unknown. Unknown view tomography (UVT) is a problem encountered in cryo-electron microscopy and in the geometric calibration of CT systems. There exists a moderate-sized literature on the 2D UVT problem, but most existing 2D UVT algorithms assume knowledge of the angle distribution which is not available usually. Our proposed methodology formulates the problem as an optimization task based on cross-validation error, to estimate the angle distribution jointly with the underlying 2D structure in an alternating fashion. We explore the algorithm's capabilities for the case of two probability distribution models: a semi-parametric mixture of von Mises densities and a probability mass function model. We evaluate our algorithm's performance under noisy projections using a PCA-based denoising technique and Graph Laplacian Tomography (GLT) driven by order statistics of the estimated distribution, to ensure near-perfect ordering, and compare our algorithm to intuitive baselines.
Submodular Framework for Structured-Sparse Optimal Transport
Jun 07, 2024Abstract:Unbalanced optimal transport (UOT) has recently gained much attention due to its flexible framework for handling un-normalized measures and its robustness properties. In this work, we explore learning (structured) sparse transport plans in the UOT setting, i.e., transport plans have an upper bound on the number of non-sparse entries in each column (structured sparse pattern) or in the whole plan (general sparse pattern). We propose novel sparsity-constrained UOT formulations building on the recently explored maximum mean discrepancy based UOT. We show that the proposed optimization problem is equivalent to the maximization of a weakly submodular function over a uniform matroid or a partition matroid. We develop efficient gradient-based discrete greedy algorithms and provide the corresponding theoretical guarantees. Empirically, we observe that our proposed greedy algorithms select a diverse support set and we illustrate the efficacy of the proposed approach in various applications.
Estimating Joint Probability Distribution With Low-Rank Tensor Decomposition, Radon Transforms and Dictionaries
Apr 18, 2023
Abstract:In this paper, we describe a method for estimating the joint probability density from data samples by assuming that the underlying distribution can be decomposed as a mixture of product densities with few mixture components. Prior works have used such a decomposition to estimate the joint density from lower-dimensional marginals, which can be estimated more reliably with the same number of samples. We combine two key ideas: dictionaries to represent 1-D densities, and random projections to estimate the joint distribution from 1-D marginals, explored separately in prior work. Our algorithm benefits from improved sample complexity over the previous dictionary-based approach by using 1-D marginals for reconstruction. We evaluate the performance of our method on estimating synthetic probability densities and compare it with the previous dictionary-based approach and Gaussian Mixture Models (GMMs). Our algorithm outperforms these other approaches in all the experimental settings.
Cooperative Multi-Agent Reinforcement Learning for Inventory Management
Apr 18, 2023Abstract:With Reinforcement Learning (RL) for inventory management (IM) being a nascent field of research, approaches tend to be limited to simple, linear environments with implementations that are minor modifications of off-the-shelf RL algorithms. Scaling these simplistic environments to a real-world supply chain comes with a few challenges such as: minimizing the computational requirements of the environment, specifying agent configurations that are representative of dynamics at real world stores and warehouses, and specifying a reward framework that encourages desirable behavior across the whole supply chain. In this work, we present a system with a custom GPU-parallelized environment that consists of one warehouse and multiple stores, a novel architecture for agent-environment dynamics incorporating enhanced state and action spaces, and a shared reward specification that seeks to optimize for a large retailer's supply chain needs. Each vertex in the supply chain graph is an independent agent that, based on its own inventory, able to place replenishment orders to the vertex upstream. The warehouse agent, aside from placing orders from the supplier, has the special property of also being able to constrain replenishment to stores downstream, which results in it learning an additional allocation sub-policy. We achieve a system that outperforms standard inventory control policies such as a base-stock policy and other RL-based specifications for 1 product, and lay out a future direction of work for multiple products.
Analysis of Tomographic Reconstruction of 2D Images using the Distribution of Unknown Projection Angles
Apr 13, 2023



Abstract:It is well known that a band-limited signal can be reconstructed from its uniformly spaced samples if the sampling rate is sufficiently high. More recently, it has been proved that one can reconstruct a 1D band-limited signal even if the exact sample locations are unknown, but given just the distribution of the sample locations and their ordering in 1D. In this work, we extend the analytical bounds on the reconstruction error in such scenarios for quasi-bandlimited signals. We also prove that the method for such a reconstruction is resilient to a certain proportion of errors in the specification of the sample location ordering. We then express the problem of tomographic reconstruction of 2D images from 1D Radon projections under unknown angles with known angle distribution, as a special case for reconstruction of quasi-bandlimited signals from samples at unknown locations with known distribution. Building upon our theoretical background, we present asymptotic bounds for 2D quasi-bandlimited image reconstruction from 1D Radon projections in the unknown angles setting, which commonly occurs in cryo-electron microscopy (cryo-EM). To the best of our knowledge, this is the first piece of work to perform such an analysis for 2D cryo-EM, even though the associated reconstruction algorithms have been known for a long time.
Joint Probability Estimation Using Tensor Decomposition and Dictionaries
Mar 03, 2022



Abstract:In this work, we study non-parametric estimation of joint probabilities of a given set of discrete and continuous random variables from their (empirically estimated) 2D marginals, under the assumption that the joint probability could be decomposed and approximated by a mixture of product densities/mass functions. The problem of estimating the joint probability density function (PDF) using semi-parametric techniques such as Gaussian Mixture Models (GMMs) is widely studied. However such techniques yield poor results when the underlying densities are mixtures of various other families of distributions such as Laplacian or generalized Gaussian, uniform, Cauchy, etc. Further, GMMs are not the best choice to estimate joint distributions which are hybrid in nature, i.e., some random variables are discrete while others are continuous. We present a novel approach for estimating the PDF using ideas from dictionary representations in signal processing coupled with low rank tensor decompositions. To the best our knowledge, this is the first work on estimating joint PDFs employing dictionaries alongside tensor decompositions. We create a dictionary of various families of distributions by inspecting the data, and use it to approximate each decomposed factor of the product in the mixture. Our approach can naturally handle hybrid $N$-dimensional distributions. We test our approach on a variety of synthetic and real datasets to demonstrate its effectiveness in terms of better classification rates and lower error rates, when compared to state of the art estimators.
A decision-tree framework to select optimal box-sizes for product shipments
Feb 09, 2022



Abstract:In package-handling facilities, boxes of varying sizes are used to ship products. Improperly sized boxes with box dimensions much larger than the product dimensions create wastage and unduly increase the shipping costs. Since it is infeasible to make unique, tailor-made boxes for each of the $N$ products, the fundamental question that confronts e-commerce companies is: How many $K << N$ cuboidal boxes need to manufactured and what should be their dimensions? In this paper, we propose a solution for the single-count shipment containing one product per box in two steps: (i) reduce it to a clustering problem in the $3$ dimensional space of length, width and height where each cluster corresponds to the group of products that will be shipped in a particular size variant, and (ii) present an efficient forward-backward decision tree based clustering method with low computational complexity on $N$ and $K$ to obtain these $K$ clusters and corresponding box dimensions. Our algorithm has multiple constituent parts, each specifically designed to achieve a high-quality clustering solution. As our method generates clusters in an incremental fashion without discarding the present solution, adding or deleting a size variant is as simple as stopping the backward pass early or executing it for one more iteration. We tested the efficacy of our approach by simulating actual single-count shipments that were transported during a month by Amazon using the proposed box dimensions. Even by just modifying the existing box dimensions and not adding a new size variant, we achieved a reduction of $4.4\%$ in the shipment volume, contributing to the decrease in non-utilized, air volume space by $2.2\%$. The reduction in shipment volume and air volume improved significantly to $10.3\%$ and $6.1\%$ when we introduced $4$ additional boxes.
Individual Treatment Effect Estimation Through Controlled Neural Network Training in Two Stages
Jan 21, 2022Abstract:We develop a Causal-Deep Neural Network (CDNN) model trained in two stages to infer causal impact estimates at an individual unit level. Using only the pre-treatment features in stage 1 in the absence of any treatment information, we learn an encoding for the covariates that best represents the outcome. In the $2^{nd}$ stage we further seek to predict the unexplained outcome from stage 1, by introducing the treatment indicator variables alongside the encoded covariates. We prove that even without explicitly computing the treatment residual, our method still satisfies the desirable local Neyman orthogonality, making it robust to small perturbations in the nuisance parameters. Furthermore, by establishing connections with the representation learning approaches, we create a framework from which multiple variants of our algorithm can be derived. We perform initial experiments on the publicly available data sets to compare these variants and get guidance in selecting the best variant of our CDNN method. On evaluating CDNN against the state-of-the-art approaches on three benchmarking datasets, we observe that CDNN is highly competitive and often yields the most accurate individual treatment effect estimates. We highlight the strong merits of CDNN in terms of its extensibility to multiple use cases.
SPOT: A framework for selection of prototypes using optimal transport
Apr 05, 2021



Abstract:In this work, we develop an optimal transport (OT) based framework to select informative prototypical examples that best represent a given target dataset. Summarizing a given target dataset via representative examples is an important problem in several machine learning applications where human understanding of the learning models and underlying data distribution is essential for decision making. We model the prototype selection problem as learning a sparse (empirical) probability distribution having the minimum OT distance from the target distribution. The learned probability measure supported on the chosen prototypes directly corresponds to their importance in representing the target data. We show that our objective function enjoys a key property of submodularity and propose an efficient greedy method that is both computationally fast and possess deterministic approximation guarantees. Empirical results on several real world benchmarks illustrate the efficacy of our approach.
Recovery of Joint Probability Distribution from one-way marginals: Low rank Tensors and Random Projections
Mar 24, 2021



Abstract:Joint probability mass function (PMF) estimation is a fundamental machine learning problem. The number of free parameters scales exponentially with respect to the number of random variables. Hence, most work on nonparametric PMF estimation is based on some structural assumptions such as clique factorization adopted by probabilistic graphical models, imposition of low rank on the joint probability tensor and reconstruction from 3-way or 2-way marginals, etc. In the present work, we link random projections of data to the problem of PMF estimation using ideas from tomography. We integrate this idea with the idea of low-rank tensor decomposition to show that we can estimate the joint density from just one-way marginals in a transformed space. We provide a novel algorithm for recovering factors of the tensor from one-way marginals, test it across a variety of synthetic and real-world datasets, and also perform MAP inference on the estimated model for classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge