Two-Dimensional Unknown View Tomography from Unknown Angle Distributions
Paper and Code
Jan 06, 2025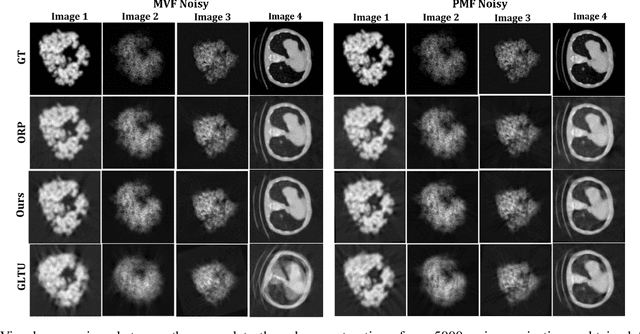
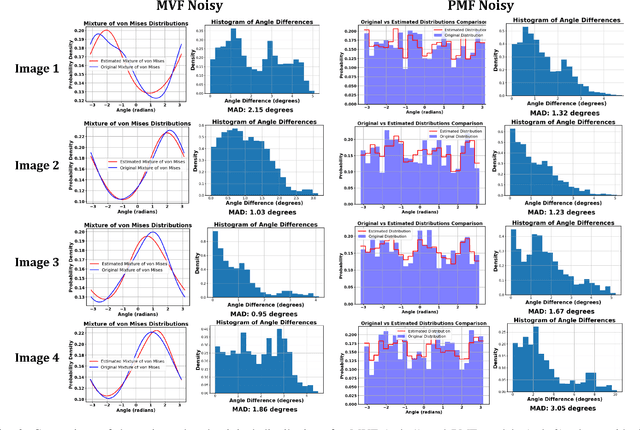


This study presents a technique for 2D tomography under unknown viewing angles when the distribution of the viewing angles is also unknown. Unknown view tomography (UVT) is a problem encountered in cryo-electron microscopy and in the geometric calibration of CT systems. There exists a moderate-sized literature on the 2D UVT problem, but most existing 2D UVT algorithms assume knowledge of the angle distribution which is not available usually. Our proposed methodology formulates the problem as an optimization task based on cross-validation error, to estimate the angle distribution jointly with the underlying 2D structure in an alternating fashion. We explore the algorithm's capabilities for the case of two probability distribution models: a semi-parametric mixture of von Mises densities and a probability mass function model. We evaluate our algorithm's performance under noisy projections using a PCA-based denoising technique and Graph Laplacian Tomography (GLT) driven by order statistics of the estimated distribution, to ensure near-perfect ordering, and compare our algorithm to intuitive baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge