Verifiable Deep Quantitative Group Testing

We present a neural network-based framework for solving the quantitative group testing (QGT) problem that achieves both high decoding accuracy and structural verifiability. In QGT, the objective is to identify a small subset of defective items among $N$ candidates using only $M \ll N$ pooled tests, each reporting the number of defectives in the tested subset. We train a multi-layer perceptron to map noisy measurement vectors to binary defect indicators, achieving accurate and robust recovery even under sparse, bounded perturbations. Beyond accuracy, we show that the trained network implicitly learns the underlying pooling structure that links items to tests, allowing this structure to be recovered directly from the network's Jacobian. This indicates that the model does not merely memorize training patterns but internalizes the true combinatorial relationships governing QGT. Our findings reveal that standard feedforward architectures can learn verifiable inverse mappings in structured combinatorial recovery problems.

Fast Debiasing of the LASSO Estimator

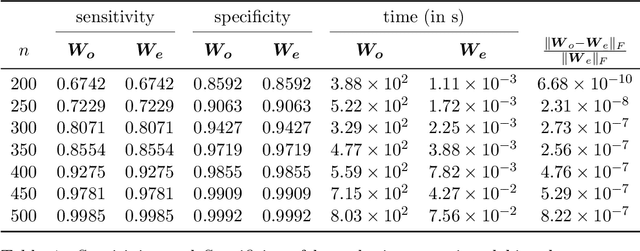
In high-dimensional sparse regression, the \textsc{Lasso} estimator offers excellent theoretical guarantees but is well-known to produce biased estimates. To address this, \cite{Javanmard2014} introduced a method to ``debias" the \textsc{Lasso} estimates for a random sub-Gaussian sensing matrix $\boldsymbol{A}$. Their approach relies on computing an ``approximate inverse" $\boldsymbol{M}$ of the matrix $\boldsymbol{A}^\top \boldsymbol{A}/n$ by solving a convex optimization problem. This matrix $\boldsymbol{M}$ plays a critical role in mitigating bias and allowing for construction of confidence intervals using the debiased \textsc{Lasso} estimates. However the computation of $\boldsymbol{M}$ is expensive in practice as it requires iterative optimization. In the presented work, we re-parameterize the optimization problem to compute a ``debiasing matrix" $\boldsymbol{W} := \boldsymbol{AM}^{\top}$ directly, rather than the approximate inverse $\boldsymbol{M}$. This reformulation retains the theoretical guarantees of the debiased \textsc{Lasso} estimates, as they depend on the \emph{product} $\boldsymbol{AM}^{\top}$ rather than on $\boldsymbol{M}$ alone. Notably, we provide a simple, computationally efficient, closed-form solution for $\boldsymbol{W}$ under similar conditions for the sensing matrix $\boldsymbol{A}$ used in the original debiasing formulation, with an additional condition that the elements of every row of $\boldsymbol{A}$ have uncorrelated entries. Also, the optimization problem based on $\boldsymbol{W}$ guarantees a unique optimal solution, unlike the original formulation based on $\boldsymbol{M}$. We verify our main result with numerical simulations.

Two-Dimensional Unknown View Tomography from Unknown Angle Distributions

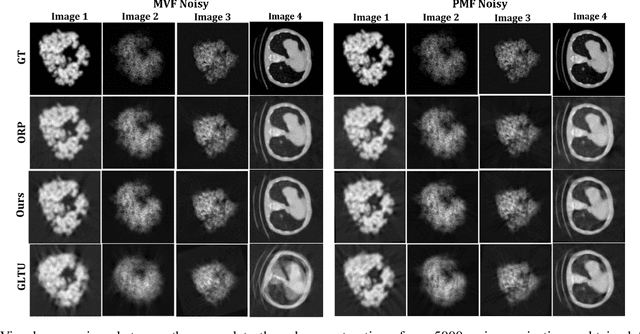
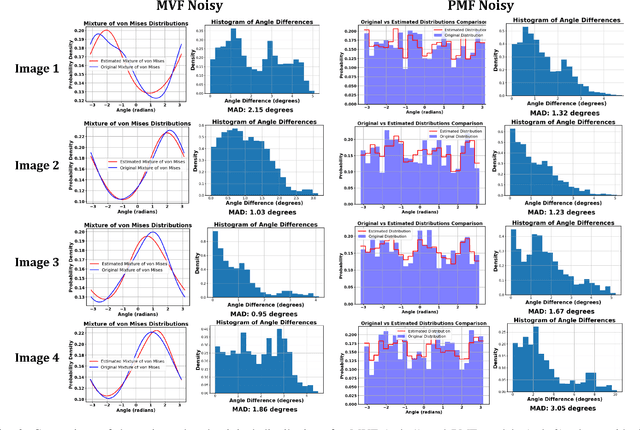
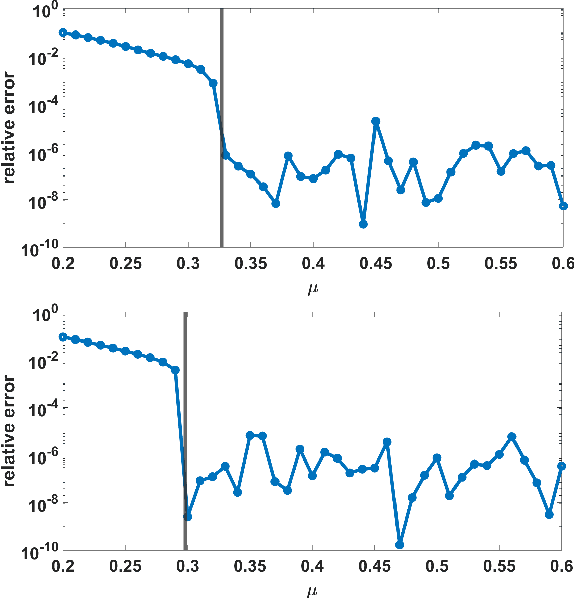
This study presents a technique for 2D tomography under unknown viewing angles when the distribution of the viewing angles is also unknown. Unknown view tomography (UVT) is a problem encountered in cryo-electron microscopy and in the geometric calibration of CT systems. There exists a moderate-sized literature on the 2D UVT problem, but most existing 2D UVT algorithms assume knowledge of the angle distribution which is not available usually. Our proposed methodology formulates the problem as an optimization task based on cross-validation error, to estimate the angle distribution jointly with the underlying 2D structure in an alternating fashion. We explore the algorithm's capabilities for the case of two probability distribution models: a semi-parametric mixture of von Mises densities and a probability mass function model. We evaluate our algorithm's performance under noisy projections using a PCA-based denoising technique and Graph Laplacian Tomography (GLT) driven by order statistics of the estimated distribution, to ensure near-perfect ordering, and compare our algorithm to intuitive baselines.

Robust Non-adaptive Group Testing under Errors in Group Membership Specifications

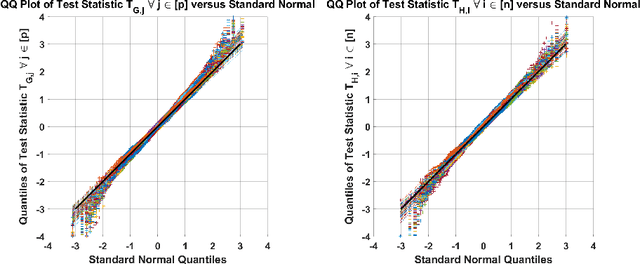
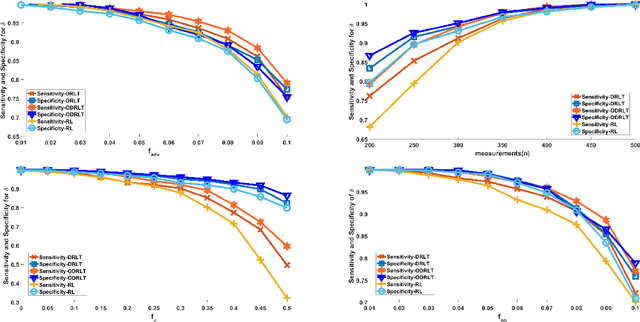
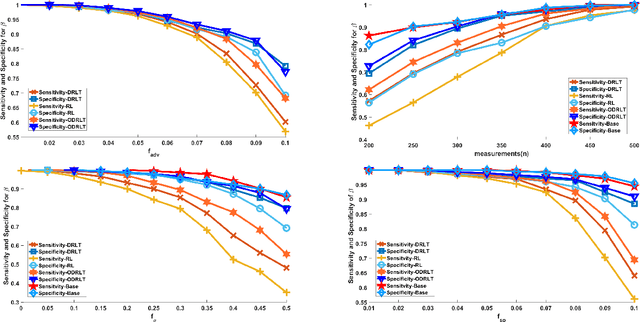
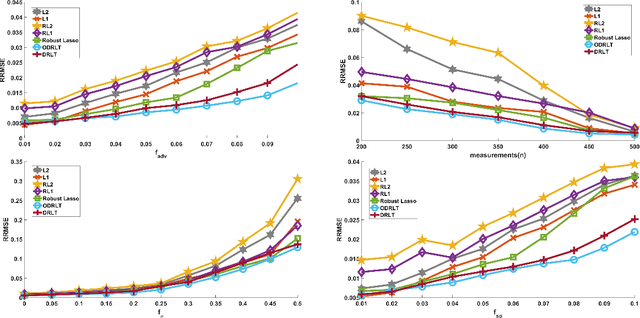
Given $p$ samples, each of which may or may not be defective, group testing (GT) aims to determine their defect status by performing tests on $n < p$ `groups', where a group is formed by mixing a subset of the $p$ samples. Assuming that the number of defective samples is very small compared to $p$, GT algorithms have provided excellent recovery of the status of all $p$ samples with even a small number of groups. Most existing methods, however, assume that the group memberships are accurately specified. This assumption may not always be true in all applications, due to various resource constraints. Such errors could occur, eg, when a technician, preparing the groups in a laboratory, unknowingly mixes together an incorrect subset of samples as compared to what was specified. We develop a new GT method, the Debiased Robust Lasso Test Method (DRLT), that handles such group membership specification errors. The proposed DRLT method is based on an approach to debias, or reduce the inherent bias in, estimates produced by Lasso, a popular and effective sparse regression technique. We also provide theoretical upper bounds on the reconstruction error produced by our estimator. Our approach is then combined with two carefully designed hypothesis tests respectively for (i) the identification of defective samples in the presence of errors in group membership specifications, and (ii) the identification of groups with erroneous membership specifications. The DRLT approach extends the literature on bias mitigation of statistical estimators such as the LASSO, to handle the important case when some of the measurements contain outliers, due to factors such as group membership specification errors. We present numerical results which show that our approach outperforms several baselines and robust regression techniques for identification of defective samples as well as erroneously specified groups.

Compressive Recovery of Signals Defined on Perturbed Graphs

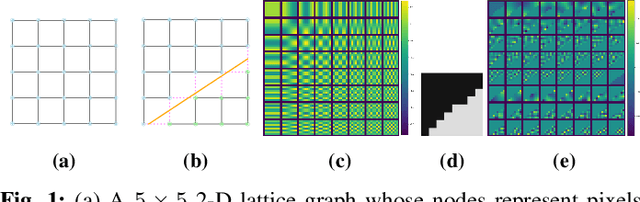
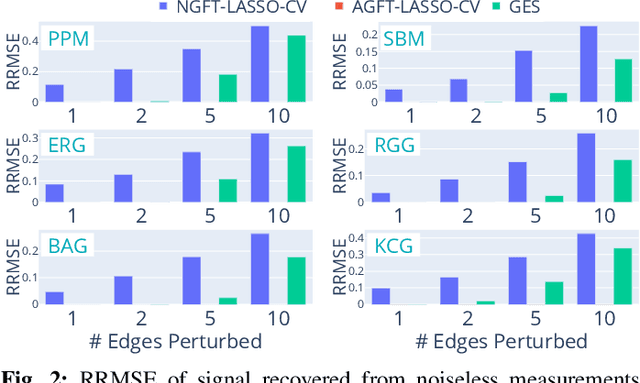
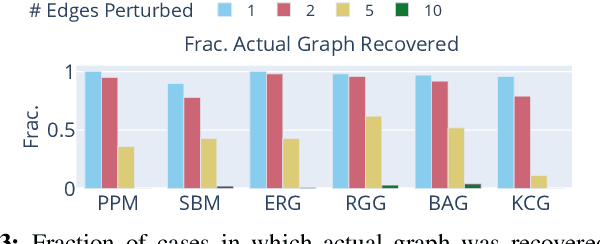
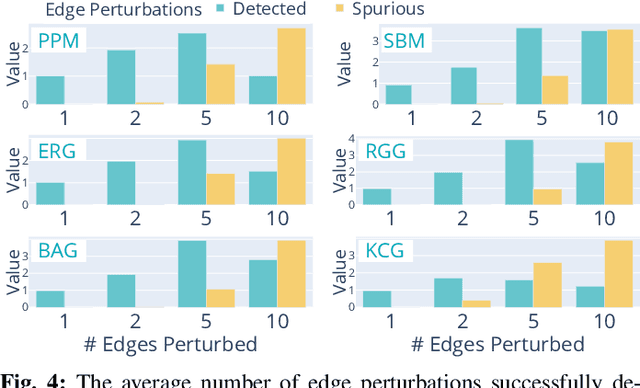
Recovery of signals with elements defined on the nodes of a graph, from compressive measurements is an important problem, which can arise in various domains such as sensor networks, image reconstruction and group testing. In some scenarios, the graph may not be accurately known, and there may exist a few edge additions or deletions relative to a ground truth graph. Such perturbations, even if small in number, significantly affect the Graph Fourier Transform (GFT). This impedes recovery of signals which may have sparse representations in the GFT bases of the ground truth graph. We present an algorithm which simultaneously recovers the signal from the compressive measurements and also corrects the graph perturbations. We analyze some important theoretical properties of the algorithm. Our approach to correction for graph perturbations is based on model selection techniques such as cross-validation in compressed sensing. We validate our algorithm on signals which have a sparse representation in the GFT bases of many commonly used graphs in the network science literature. An application to compressive image reconstruction is also presented, where graph perturbations are modeled as undesirable graph edges linking pixels with significant intensity difference. In all experiments, our algorithm clearly outperforms baseline techniques which either ignore the perturbations or use first order approximations to the perturbations in the GFT bases.

Group Testing for Accurate and Efficient Range-Based Near Neighbor Search : An Adaptive Binary Splitting Approach

This work presents an adaptive group testing framework for the range-based high dimensional near neighbor search problem. The proposed method detects high-similarity vectors from an extensive collection of high dimensional vectors, where each vector represents an image descriptor. Our method efficiently marks each item in the collection as neighbor or non-neighbor on the basis of a cosine distance threshold without exhaustive search. Like other methods in the domain of large scale retrieval, our approach exploits the assumption that most of the items in the collection are unrelated to the query. Unlike other methods, it does not assume a large difference between the cosine similarity of the query vector with the least related neighbor and that with the least unrelated non-neighbor. Following the procedure of binary splitting, a multi-stage adaptive group testing algorithm, we split the set of items to be searched into half at each step, and perform dot product tests on smaller and smaller subsets, many of which we are able to prune away. We experimentally show that our method achieves a speed-up over exhaustive search by a factor of more than ten with an accuracy same as that of exhaustive search, on a variety of large datasets. We present a theoretical analysis of the expected number of distance computations per query and the probability that a pool with a certain number of members will be pruned. In this way, our method exploits very useful and practical distributional properties unlike other methods. In our method, all required data structures are created purely offline. Moreover, our method does not impose any strong assumptions on the number of true near neighbors, is adaptible to streaming settings where new vectors are dynamically added to the database, and does not require any parameter tuning.

Unlabelled Sensing with Priors: Algorithm and Bounds

In this study, we consider a variant of unlabelled sensing where the measurements are sparsely permuted, and additionally, a few correspondences are known. We present an estimator to solve for the unknown vector. We derive a theoretical upper bound on the $\ell_2$ reconstruction error of the unknown vector. Through numerical experiments, we demonstrate that the additional known correspondences result in a significant improvement in the reconstruction error. Additionally, we compare our estimator with the classical robust regression estimator and we find that our method outperforms it on the normalized reconstruction error metric by up to $20\%$ in the high permutation regimes $(>30\%)$. Lastly, we showcase the practical utility of our framework on a non-rigid motion estimation problem. We show that using a few manually annotated points along point pairs with the key-point (SIFT-based) descriptor pairs with unknown or incorrectly known correspondences can improve motion estimation.

Efficient Neural Network based Classification and Outlier Detection for Image Moderation using Compressed Sensing and Group Testing

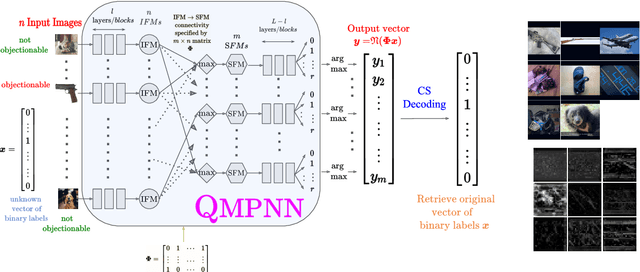
Popular social media platforms employ neural network based image moderation engines to classify images uploaded on them as having potentially objectionable content. Such moderation engines must answer a large number of queries with heavy computational cost, even though the actual number of images with objectionable content is usually a tiny fraction. Inspired by recent work on Neural Group Testing, we propose an approach which exploits this fact to reduce the overall computational cost of such engines using the technique of Compressed Sensing (CS). We present the quantitative matrix-pooled neural network (QMPNN), which takes as input $n$ images, and a $m \times n$ binary pooling matrix with $m < n$, whose rows indicate $m$ pools of images i.e. selections of $r$ images out of $n$. The QMPNN efficiently outputs the product of this matrix with the unknown sparse binary vector indicating whether each image is objectionable or not, i.e. it outputs the number of objectionable images in each pool. For suitable matrices, this is decoded using CS decoding algorithms to predict which images were objectionable. The computational cost of running the QMPNN and the CS algorithms is significantly lower than the cost of using a neural network with the same number of parameters separately on each image to classify the images, which we demonstrate via extensive experiments. Our technique is inherently resilient to moderate levels of errors in the prediction from the QMPNN. Furthermore, we present pooled deep outlier detection, which brings CS and group testing techniques to deep outlier detection, to provide for the case when the objectionable images do not belong to a set of pre-defined classes. This technique enables efficient automated moderation of off-topic images shared on topical forums dedicated to sharing images of a certain single class, many of which are currently human-moderated.

Estimating Joint Probability Distribution With Low-Rank Tensor Decomposition, Radon Transforms and Dictionaries

In this paper, we describe a method for estimating the joint probability density from data samples by assuming that the underlying distribution can be decomposed as a mixture of product densities with few mixture components. Prior works have used such a decomposition to estimate the joint density from lower-dimensional marginals, which can be estimated more reliably with the same number of samples. We combine two key ideas: dictionaries to represent 1-D densities, and random projections to estimate the joint distribution from 1-D marginals, explored separately in prior work. Our algorithm benefits from improved sample complexity over the previous dictionary-based approach by using 1-D marginals for reconstruction. We evaluate the performance of our method on estimating synthetic probability densities and compare it with the previous dictionary-based approach and Gaussian Mixture Models (GMMs). Our algorithm outperforms these other approaches in all the experimental settings.

Analysis of Tomographic Reconstruction of 2D Images using the Distribution of Unknown Projection Angles

It is well known that a band-limited signal can be reconstructed from its uniformly spaced samples if the sampling rate is sufficiently high. More recently, it has been proved that one can reconstruct a 1D band-limited signal even if the exact sample locations are unknown, but given just the distribution of the sample locations and their ordering in 1D. In this work, we extend the analytical bounds on the reconstruction error in such scenarios for quasi-bandlimited signals. We also prove that the method for such a reconstruction is resilient to a certain proportion of errors in the specification of the sample location ordering. We then express the problem of tomographic reconstruction of 2D images from 1D Radon projections under unknown angles with known angle distribution, as a special case for reconstruction of quasi-bandlimited signals from samples at unknown locations with known distribution. Building upon our theoretical background, we present asymptotic bounds for 2D quasi-bandlimited image reconstruction from 1D Radon projections in the unknown angles setting, which commonly occurs in cryo-electron microscopy (cryo-EM). To the best of our knowledge, this is the first piece of work to perform such an analysis for 2D cryo-EM, even though the associated reconstruction algorithms have been known for a long time.