Compressed Sensing Based Residual Recovery Algorithms and Hardware for Modulo Sampling

Analog-to-Digital Converters (ADCs) are essential components in modern data acquisition systems. A key design challenge is accommodating high dynamic range (DR) input signals without clipping. Existing solutions, such as oversampling, automatic gain control (AGC), and compander-based methods, have limitations in handling high-DR signals. Recently, the Unlimited Sampling Framework (USF) has emerged as a promising alternative. It uses a non-linear modulo operator to map high-DR signals within the ADC range. Existing recovery algorithms, such as higher-order differences (HODs), prediction-based methods, and beyond bandwidth residual recovery (B2R2), have shown potential but are either noise-sensitive, require high sampling rates, or are computationally intensive. To address these challenges, we propose LASSO-B2R2, a fast and robust recovery algorithm. Specifically, we demonstrate that the first-order difference of the residual (the difference between the folded and original samples) is sparse, and we derive an upper bound on its sparsity. This insight allows us to formulate the recovery as a sparse signal reconstruction problem using the least absolute shrinkage and selection operator (LASSO). Numerical simulations show that LASSO-B2R2 outperforms prior methods in terms of speed and robustness, though it requires a higher sampling rate at lower DR. To overcome this, we introduce the bits distribution mechanism, which allocates 1 bit from the total bit budget to identify modulo folding events. This reduces the recovery problem to a simple pseudo-inverse computation, significantly enhancing computational efficiency. Finally, we validate our approach through numerical simulations and a hardware prototype that captures 1-bit folding information, demonstrating its practical feasibility.

Subsampling of Correlated Graph Signals

Graph signals are functions of the underlying graph. When the edge-weight between a pair of nodes is high, the corresponding signals generally have a higher correlation. As a result, the signals can be represented in terms of a graph-based generative model. The question then arises whether measurements can be obtained on a few nodes and whether the correlation structure between the signals can be used to reconstruct the graph signal on the remaining nodes. We show that node subsampling is always possible for graph signals obtained through a generative model. Further, a method to determine the number of nodes to select is proposed based on the tolerable error. A correlation-based fast greedy algorithm is developed for selecting the nodes. Finally, we verify the proposed method on different deterministic and random graphs, and show that near-perfect reconstruction is possible with node subsampling.

Blind-Adaptive Quantizers

Sampling and quantization are crucial in digital signal processing, but quantization introduces errors, particularly due to distribution mismatch between input signals and quantizers. Existing methods to reduce this error require precise knowledge of the input's distribution, which is often unavailable. To address this, we propose a blind and adaptive method that minimizes distribution mismatch without prior knowledge of the input distribution. Our approach uses a nonlinear transformation with amplification and modulo-folding, followed by a uniform quantizer. Theoretical analysis shows that sufficient amplification makes the output distribution of modulo-folding nearly uniform, reducing mismatch across various distributions, including Gaussian, exponential, and uniform. To recover the true quantized samples, we suggest using existing unfolding techniques, which, despite requiring significant oversampling, effectively reduce mismatch and quantization error, offering a favorable trade-off similar to predictive coding strategies.

Power-Efficient Sampling

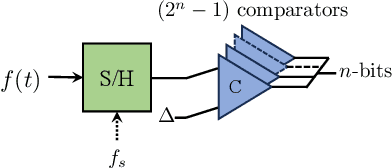
Analog-to-digital converters (ADCs) facilitate the conversion of analog signals into a digital format. While the specific designs and settings of ADCs can vary depending on their applications, it is crucial in many modern applications to minimize their power consumption. The significance of low-power ADCs is particularly evident in fields like mobile and handheld devices reliant on battery operation. Key parameters of the ADCs that dictate the ADC's power are its sampling rate, dynamic range, and number of quantization bits. Typically, these parameters are required to be higher than a threshold value but can be reduced by using the structure of the signal and by leveraging preprocessing and the system application needs. In this review, we discuss four approaches relevant to a variety of applications.

Modulation For Modulo: A Sampling-Efficient High-Dynamic Range ADC

In high-dynamic range (HDR) analog-to-digital converters (ADCs), having many quantization bits minimizes quantization errors but results in high bit rates, limiting their application scope. A strategy combining modulo-folding with a low-DR ADC can create an efficient HDR-ADC with fewer bits. However, this typically demands oversampling, increasing the overall bit rate. An alternative method using phase modulation (PM) achieves HDR-ADC functionality by modulating the phase of a carrier signal with the analog input. This allows a low-DR ADC with fewer bits. We've derived identifiability results enabling reconstruction of the original signal from PM samples acquired at the Nyquist rate, adaptable to various signals and non-uniform sampling. Using discrete phase demodulation algorithms for practical implementation, our PM-based approach doesn't require oversampling in noise-free conditions, contrasting with modulo-based ADCs. With noise, our PM-based HDR method demonstrates efficiency with lower reconstruction errors and reduced sampling rates. Our hardware prototype illustrates reconstructing signals ten times greater than the ADC's DR from Nyquist rate samples, potentially replacing high-bit rate HDR-ADCs while meeting existing bit rate needs.

Unlabelled Sensing with Priors: Algorithm and Bounds

In this study, we consider a variant of unlabelled sensing where the measurements are sparsely permuted, and additionally, a few correspondences are known. We present an estimator to solve for the unknown vector. We derive a theoretical upper bound on the $\ell_2$ reconstruction error of the unknown vector. Through numerical experiments, we demonstrate that the additional known correspondences result in a significant improvement in the reconstruction error. Additionally, we compare our estimator with the classical robust regression estimator and we find that our method outperforms it on the normalized reconstruction error metric by up to $20\%$ in the high permutation regimes $(>30\%)$. Lastly, we showcase the practical utility of our framework on a non-rigid motion estimation problem. We show that using a few manually annotated points along point pairs with the key-point (SIFT-based) descriptor pairs with unknown or incorrectly known correspondences can improve motion estimation.

Greedy Selection for Heterogeneous Sensors

In large-scale sensor networks, simultaneously operating all the sensors is power-consuming and computationally expensive. It is often necessary to adaptively select or activate a few sensors at a time. A greedy selection (GS) algorithm is widely used to select sensors in homogeneous sensor networks. It is guaranteed a worst-case performance $(1 - 1/e) \approx 63\%$ of the optimal solution when the performance metric is submodular. However, in heterogeneous sensor networks (HSNs), where the sensors can have different precision and operating costs, the sensor selection problem has not been explored sufficiently well. In this paper, a joint greedy selection (JGS) algorithm is proposed to compute the best possible subset of sensors in HSNs. We derive theoretical guarantees for the worst-case error of JGS for submodular performance metrics for an HSN consisting of two sets of sensors: a set with expensive high-precision sensors and a set of cheap low-precision sensors. A limit on the number of sensors from each class is stipulated, and we propose algorithms to solve the sensor selection problem and assess their theoretical performance guarantees. We show that the worst-case relative error approaches $(1 - 1/e)$ when the stipulated number of high-precision sensors is much smaller than that of low-precision sensors. To compare the JGS algorithm with existing methods, we propose a frame potential-based submodular performance metric that considers both the correlation among the measurements as well as the heterogeneity of the sensors. Experimentally, we show that the JGS algorithm results in $4$-$10$ dB lower error than existing methods.

A Hardware Prototype of Wideband High-Dynamic Range ADC

Key parameters of analog-to-digital converters (ADCs) are their sampling rate and dynamic range. Power consumption and cost of an ADC are directly proportional to the sampling rate; hence, it is desirable to keep it as low as possible. The dynamic range of an ADC also plays an important role, and ideally, it should be greater than the signal's; otherwise, the signal will be clipped. To avoid clipping, modulo folding can be used before sampling, followed by an unfolding algorithm to recover the true signal. In this paper, we present a modulo hardware prototype that can be used before sampling to avoid clipping. Our modulo hardware operates prior to the sampling mechanism and can fold higher frequency signals compared to existing hardware. We present a detailed design of the hardware and also address key issues that arise during implementation. In terms of applications, we show the reconstruction of finite-rate-of-innovation signals which are beyond the dynamic range of the ADC. Our system operates at six times below the Nyquist rate of the signal and can accommodate eight-times larger signals than the ADC's dynamic range.

Learning Filter-Based Compressed Blind-Deconvolution

The problem of sparse multichannel blind deconvolution (S-MBD) arises frequently in many engineering applications such as radar/sonar/ultrasound imaging. To reduce its computational and implementation cost, we propose a compression method that enables blind recovery from much fewer measurements with respect to the full received signal in time. The proposed compression measures the signal through a filter followed by a subsampling, allowing for a significant reduction in implementation cost. We derive theoretical guarantees for the identifiability and recovery of a sparse filter from compressed measurements. Our results allow for the design of a wide class of compression filters. We, then, propose a data-driven unrolled learning framework to learn the compression filter and solve the S-MBD problem. The encoder is a recurrent inference network that maps compressed measurements into an estimate of sparse filters. We demonstrate that our unrolled learning method is more robust to choices of source shapes and has better recovery performance compared to optimization-based methods. Finally, in applications with limited data (fewshot learning), we highlight the superior generalization capability of unrolled learning compared to conventional deep learning.

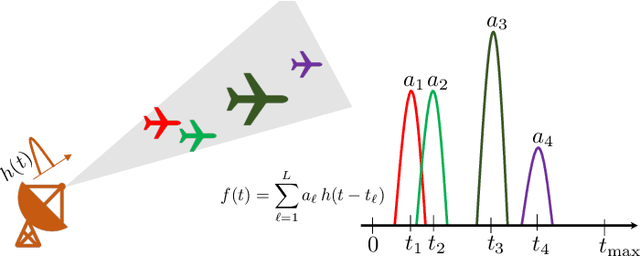
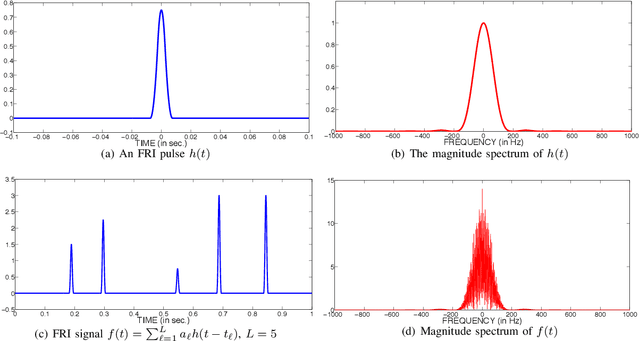
Modulo Sampling of FRI Signals

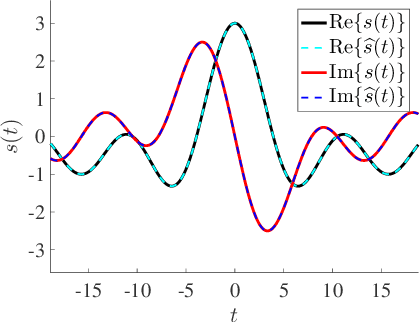
The dynamic range of an analog-to-digital converter (ADC) is critical during sampling of analog signals. A modulo operation prior to sampling can be used to enhance the effective dynamic range of the ADC. Further, sampling rate of ADC too plays a crucial role and it is desirable to reduce it. Finite-rate-of-innovation (FRI) signal model, which is ubiquitous in many applications, can be used to reduce the sampling rate. In the context of modulo folding for FRI sampling, existing works operate at a very high sampling rate compared to the rate of innovation (RoI) and require a large number of samples compared to the degrees of freedom (DoF) of the FRI signal. Moreover, these approaches use infinite length filters that are practically infeasible. We consider the FRI sampling problem with a compactly supported kernel under the modulo framework. We derive theoretical guarantees and show that FRI signals could be uniquely identified by sampling above the RoI. The number of samples for identifiability is equal to the DoF. We propose a practical algorithm to estimate the FRI parameters from the modulo samples. We show that the proposed approach has the lowest error in estimating the FRI parameters while operating with the lowest number of samples and sampling rates compared to existing techniques. The results are helpful in designing cost-effective, high-dynamic-range ADCs for FRI signals.