Modulo Sampling of FRI Signals

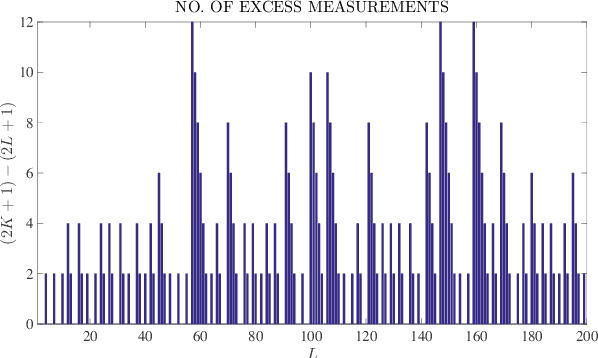
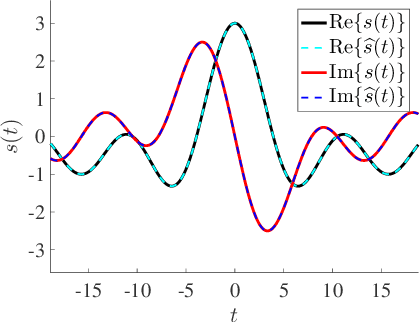
The dynamic range of an analog-to-digital converter (ADC) is critical during sampling of analog signals. A modulo operation prior to sampling can be used to enhance the effective dynamic range of the ADC. Further, sampling rate of ADC too plays a crucial role and it is desirable to reduce it. Finite-rate-of-innovation (FRI) signal model, which is ubiquitous in many applications, can be used to reduce the sampling rate. In the context of modulo folding for FRI sampling, existing works operate at a very high sampling rate compared to the rate of innovation (RoI) and require a large number of samples compared to the degrees of freedom (DoF) of the FRI signal. Moreover, these approaches use infinite length filters that are practically infeasible. We consider the FRI sampling problem with a compactly supported kernel under the modulo framework. We derive theoretical guarantees and show that FRI signals could be uniquely identified by sampling above the RoI. The number of samples for identifiability is equal to the DoF. We propose a practical algorithm to estimate the FRI parameters from the modulo samples. We show that the proposed approach has the lowest error in estimating the FRI parameters while operating with the lowest number of samples and sampling rates compared to existing techniques. The results are helpful in designing cost-effective, high-dynamic-range ADCs for FRI signals.