Demba Ba
Block-Recurrent Dynamics in Vision Transformers
Dec 23, 2025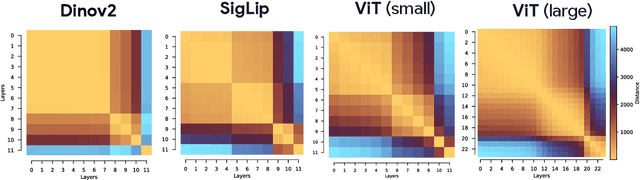
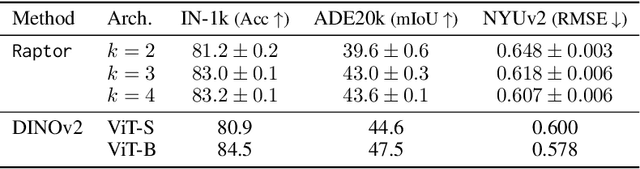

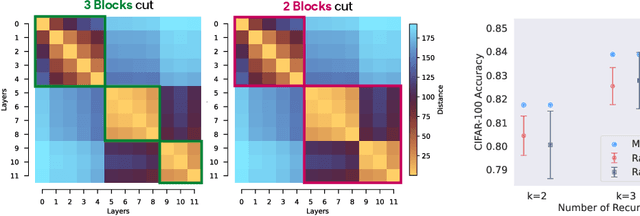
Abstract:As Vision Transformers (ViTs) become standard vision backbones, a mechanistic account of their computational phenomenology is essential. Despite architectural cues that hint at dynamical structure, there is no settled framework that interprets Transformer depth as a well-characterized flow. In this work, we introduce the Block-Recurrent Hypothesis (BRH), arguing that trained ViTs admit a block-recurrent depth structure such that the computation of the original $L$ blocks can be accurately rewritten using only $k \ll L$ distinct blocks applied recurrently. Across diverse ViTs, between-layer representational similarity matrices suggest few contiguous phases. To determine whether these phases reflect genuinely reusable computation, we train block-recurrent surrogates of pretrained ViTs: Recurrent Approximations to Phase-structured TransfORmers (Raptor). In small-scale, we demonstrate that stochastic depth and training promote recurrent structure and subsequently correlate with our ability to accurately fit Raptor. We then provide an empirical existence proof for BRH by training a Raptor model to recover $96\%$ of DINOv2 ImageNet-1k linear probe accuracy in only 2 blocks at equivalent computational cost. Finally, we leverage our hypothesis to develop a program of Dynamical Interpretability. We find i) directional convergence into class-dependent angular basins with self-correcting trajectories under small perturbations, ii) token-specific dynamics, where cls executes sharp late reorientations while patch tokens exhibit strong late-stage coherence toward their mean direction, and iii) a collapse to low rank updates in late depth, consistent with convergence to low-dimensional attractors. Altogether, we find a compact recurrent program emerges along ViT depth, pointing to a low-complexity normative solution that enables these models to be studied through principled dynamical systems analysis.
Evaluating Sparse Autoencoders: From Shallow Design to Matching Pursuit
Jun 05, 2025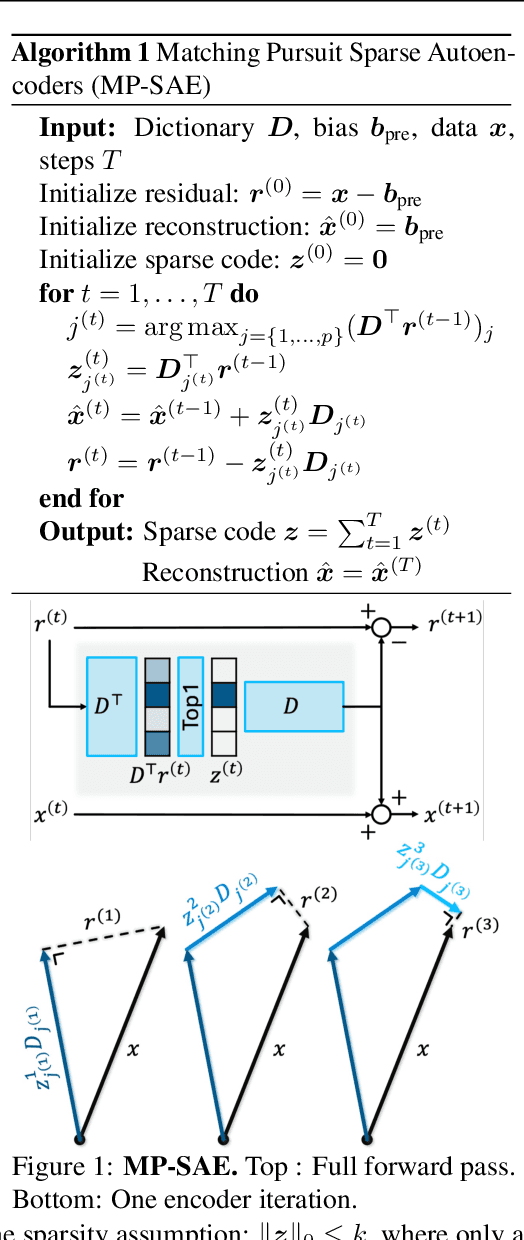
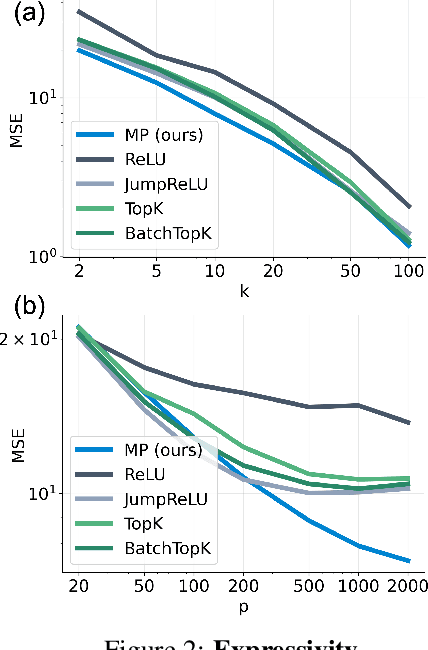

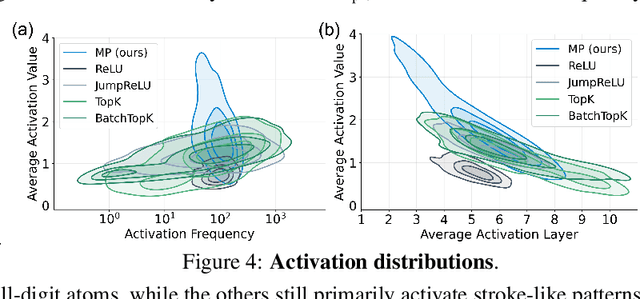
Abstract:Sparse autoencoders (SAEs) have recently become central tools for interpretability, leveraging dictionary learning principles to extract sparse, interpretable features from neural representations whose underlying structure is typically unknown. This paper evaluates SAEs in a controlled setting using MNIST, which reveals that current shallow architectures implicitly rely on a quasi-orthogonality assumption that limits the ability to extract correlated features. To move beyond this, we introduce a multi-iteration SAE by unrolling Matching Pursuit (MP-SAE), enabling the residual-guided extraction of correlated features that arise in hierarchical settings such as handwritten digit generation while guaranteeing monotonic improvement of the reconstruction as more atoms are selected.
Projecting Assumptions: The Duality Between Sparse Autoencoders and Concept Geometry
Mar 03, 2025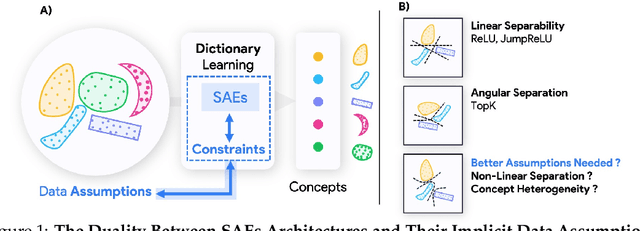
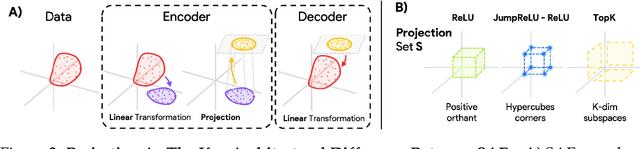
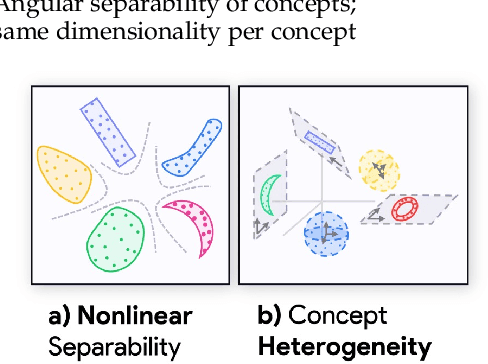

Abstract:Sparse Autoencoders (SAEs) are widely used to interpret neural networks by identifying meaningful concepts from their representations. However, do SAEs truly uncover all concepts a model relies on, or are they inherently biased toward certain kinds of concepts? We introduce a unified framework that recasts SAEs as solutions to a bilevel optimization problem, revealing a fundamental challenge: each SAE imposes structural assumptions about how concepts are encoded in model representations, which in turn shapes what it can and cannot detect. This means different SAEs are not interchangeable -- switching architectures can expose entirely new concepts or obscure existing ones. To systematically probe this effect, we evaluate SAEs across a spectrum of settings: from controlled toy models that isolate key variables, to semi-synthetic experiments on real model activations and finally to large-scale, naturalistic datasets. Across this progression, we examine two fundamental properties that real-world concepts often exhibit: heterogeneity in intrinsic dimensionality (some concepts are inherently low-dimensional, others are not) and nonlinear separability. We show that SAEs fail to recover concepts when these properties are ignored, and we design a new SAE that explicitly incorporates both, enabling the discovery of previously hidden concepts and reinforcing our theoretical insights. Our findings challenge the idea of a universal SAE and underscores the need for architecture-specific choices in model interpretability. Overall, we argue an SAE does not just reveal concepts -- it determines what can be seen at all.
Archetypal SAE: Adaptive and Stable Dictionary Learning for Concept Extraction in Large Vision Models
Feb 18, 2025Abstract:Sparse Autoencoders (SAEs) have emerged as a powerful framework for machine learning interpretability, enabling the unsupervised decomposition of model representations into a dictionary of abstract, human-interpretable concepts. However, we reveal a fundamental limitation: existing SAEs exhibit severe instability, as identical models trained on similar datasets can produce sharply different dictionaries, undermining their reliability as an interpretability tool. To address this issue, we draw inspiration from the Archetypal Analysis framework introduced by Cutler & Breiman (1994) and present Archetypal SAEs (A-SAE), wherein dictionary atoms are constrained to the convex hull of data. This geometric anchoring significantly enhances the stability of inferred dictionaries, and their mildly relaxed variants RA-SAEs further match state-of-the-art reconstruction abilities. To rigorously assess dictionary quality learned by SAEs, we introduce two new benchmarks that test (i) plausibility, if dictionaries recover "true" classification directions and (ii) identifiability, if dictionaries disentangle synthetic concept mixtures. Across all evaluations, RA-SAEs consistently yield more structured representations while uncovering novel, semantically meaningful concepts in large-scale vision models.
Traveling Waves Integrate Spatial Information Into Spectral Representations
Feb 09, 2025Abstract:Traveling waves are widely observed in the brain, but their precise computational function remains unclear. One prominent hypothesis is that they enable the transfer and integration of spatial information across neural populations. However, few computational models have explored how traveling waves might be harnessed to perform such integrative processing. Drawing inspiration from the famous ``Can one hear the shape of a drum?'' problem -- which highlights how spectral modes encode geometric information -- we introduce a set of convolutional recurrent neural networks that learn to produce traveling waves in their hidden states in response to visual stimuli. By applying a spectral decomposition to these wave-like activations, we obtain a powerful new representational space that outperforms equivalently local feed-forward networks on tasks requiring global spatial context. In particular, we observe that traveling waves effectively expand the receptive field of locally connected neurons, supporting long-range encoding and communication of information. We demonstrate that models equipped with this mechanism and spectral readouts solve visual semantic segmentation tasks demanding global integration, where local feed-forward models fail. As a first step toward traveling-wave-based representations in artificial networks, our findings suggest potential efficiency benefits and offer a new framework for connecting to biological recordings of neural activity.
An Efficient Algorithm for Clustered Multi-Task Compressive Sensing
Sep 30, 2023Abstract:This paper considers clustered multi-task compressive sensing, a hierarchical model that solves multiple compressive sensing tasks by finding clusters of tasks that leverage shared information to mutually improve signal reconstruction. The existing inference algorithm for this model is computationally expensive and does not scale well in high dimensions. The main bottleneck involves repeated matrix inversion and log-determinant computation for multiple large covariance matrices. We propose a new algorithm that substantially accelerates model inference by avoiding the need to explicitly compute these covariance matrices. Our approach combines Monte Carlo sampling with iterative linear solvers. Our experiments reveal that compared to the existing baseline, our algorithm can be up to thousands of times faster and an order of magnitude more memory-efficient.
Probabilistic Unrolling: Scalable, Inverse-Free Maximum Likelihood Estimation for Latent Gaussian Models
Jun 05, 2023



Abstract:Latent Gaussian models have a rich history in statistics and machine learning, with applications ranging from factor analysis to compressed sensing to time series analysis. The classical method for maximizing the likelihood of these models is the expectation-maximization (EM) algorithm. For problems with high-dimensional latent variables and large datasets, EM scales poorly because it needs to invert as many large covariance matrices as the number of data points. We introduce probabilistic unrolling, a method that combines Monte Carlo sampling with iterative linear solvers to circumvent matrix inversion. Our theoretical analyses reveal that unrolling and backpropagation through the iterations of the solver can accelerate gradient estimation for maximum likelihood estimation. In experiments on simulated and real data, we demonstrate that probabilistic unrolling learns latent Gaussian models up to an order of magnitude faster than gradient EM, with minimal losses in model performance.
* 29 pages, 4 figures
Learning Linear Groups in Neural Networks
May 29, 2023Abstract:Employing equivariance in neural networks leads to greater parameter efficiency and improved generalization performance through the encoding of domain knowledge in the architecture; however, the majority of existing approaches require an a priori specification of the desired symmetries. We present a neural network architecture, Linear Group Networks (LGNs), for learning linear groups acting on the weight space of neural networks. Linear groups are desirable due to their inherent interpretability, as they can be represented as finite matrices. LGNs learn groups without any supervision or knowledge of the hidden symmetries in the data and the groups can be mapped to well known operations in machine learning. We use LGNs to learn groups on multiple datasets while considering different downstream tasks; we demonstrate that the linear group structure depends on both the data distribution and the considered task.
Sparse, Geometric Autoencoder Models of V1
Feb 22, 2023
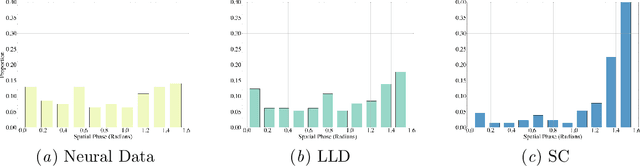
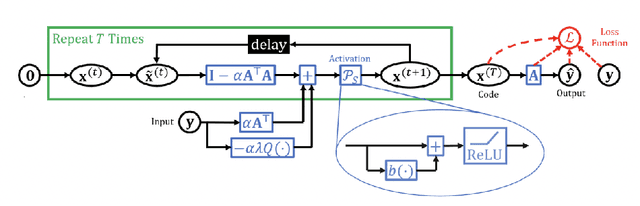
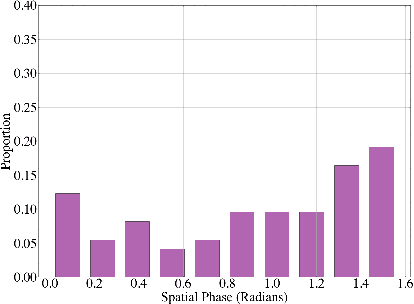
Abstract:The classical sparse coding model represents visual stimuli as a linear combination of a handful of learned basis functions that are Gabor-like when trained on natural image data. However, the Gabor-like filters learned by classical sparse coding far overpredict well-tuned simple cell receptive field (SCRF) profiles. A number of subsequent models have either discarded the sparse dictionary learning framework entirely or have yet to take advantage of the surge in unrolled, neural dictionary learning architectures. A key missing theme of these updates is a stronger notion of \emph{structured sparsity}. We propose an autoencoder architecture whose latent representations are implicitly, locally organized for spectral clustering, which begets artificial neurons better matched to observed primate data. The weighted-$\ell_1$ (WL) constraint in the autoencoder objective function maintains core ideas of the sparse coding framework, yet also offers a promising path to describe the differentiation of receptive fields in terms of a discriminative hierarchy in future work.
Learning unfolded networks with a cyclic group structure
Nov 16, 2022



Abstract:Deep neural networks lack straightforward ways to incorporate domain knowledge and are notoriously considered black boxes. Prior works attempted to inject domain knowledge into architectures implicitly through data augmentation. Building on recent advances on equivariant neural networks, we propose networks that explicitly encode domain knowledge, specifically equivariance with respect to rotations. By using unfolded architectures, a rich framework that originated from sparse coding and has theoretical guarantees, we present interpretable networks with sparse activations. The equivariant unfolded networks compete favorably with baselines, with only a fraction of their parameters, as showcased on (rotated) MNIST and CIFAR-10.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge