An explicit operator explains end-to-end computation in the modern neural networks used for sequence and language modeling

We establish a mathematical correspondence between state space models, a state-of-the-art architecture for capturing long-range dependencies in data, and an exactly solvable nonlinear oscillator network. As a specific example of this general correspondence, we analyze the diagonal linear time-invariant implementation of the Structured State Space Sequence model (S4). The correspondence embeds S4D, a specific implementation of S4, into a ring network topology, in which recent inputs are encoded, as waves of activity traveling over the one-dimensional spatial layout of the network. We then derive an exact operator expression for the full forward pass of S4D, yielding an analytical characterization of its complete input-output map. This expression reveals that the nonlinear decoder in the system induces interactions between these information-carrying waves that enable classifying real-world sequences. These results generalize across modern SSM architectures, and show that they admit an exact mathematical description with a clear physical interpretation. These insights enable a new level of interpretability for these systems in terms of nonlinear oscillator networks.

Traveling Waves Integrate Spatial Information Into Spectral Representations

Traveling waves are widely observed in the brain, but their precise computational function remains unclear. One prominent hypothesis is that they enable the transfer and integration of spatial information across neural populations. However, few computational models have explored how traveling waves might be harnessed to perform such integrative processing. Drawing inspiration from the famous ``Can one hear the shape of a drum?'' problem -- which highlights how spectral modes encode geometric information -- we introduce a set of convolutional recurrent neural networks that learn to produce traveling waves in their hidden states in response to visual stimuli. By applying a spectral decomposition to these wave-like activations, we obtain a powerful new representational space that outperforms equivalently local feed-forward networks on tasks requiring global spatial context. In particular, we observe that traveling waves effectively expand the receptive field of locally connected neurons, supporting long-range encoding and communication of information. We demonstrate that models equipped with this mechanism and spectral readouts solve visual semantic segmentation tasks demanding global integration, where local feed-forward models fail. As a first step toward traveling-wave-based representations in artificial networks, our findings suggest potential efficiency benefits and offer a new framework for connecting to biological recordings of neural activity.

Image segmentation with traveling waves in an exactly solvable recurrent neural network

We study image segmentation using spatiotemporal dynamics in a recurrent neural network where the state of each unit is given by a complex number. We show that this network generates sophisticated spatiotemporal dynamics that can effectively divide an image into groups according to a scene's structural characteristics. Using an exact solution of the recurrent network's dynamics, we present a precise description of the mechanism underlying object segmentation in this network, providing a clear mathematical interpretation of how the network performs this task. We then demonstrate a simple algorithm for object segmentation that generalizes across inputs ranging from simple geometric objects in grayscale images to natural images. Object segmentation across all images is accomplished with one recurrent neural network that has a single, fixed set of weights. This demonstrates the expressive potential of recurrent neural networks when constructed using a mathematical approach that brings together their structure, dynamics, and computation.

An exact mathematical description of computation with transient spatiotemporal dynamics in a complex-valued neural network

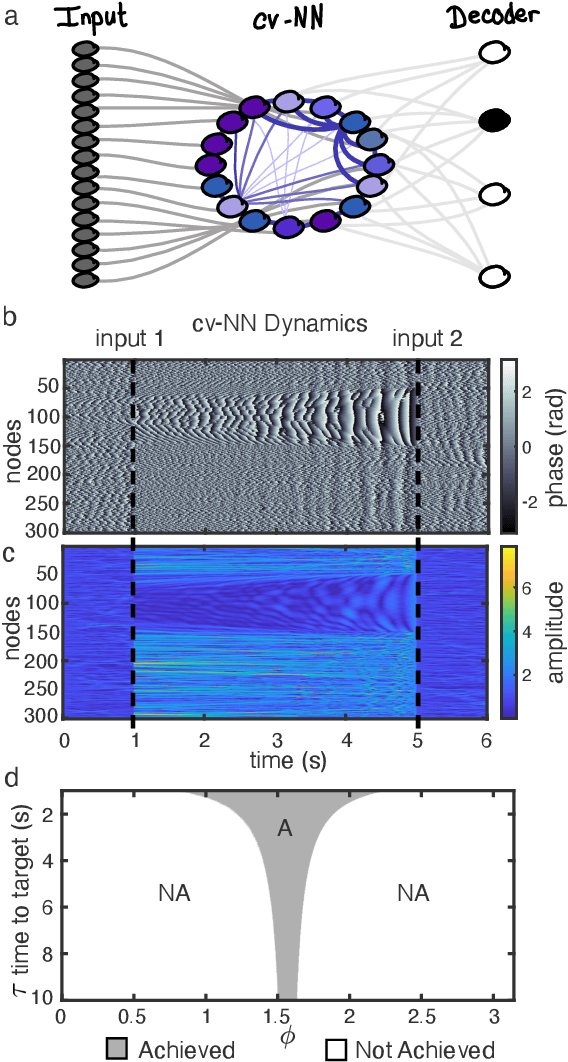
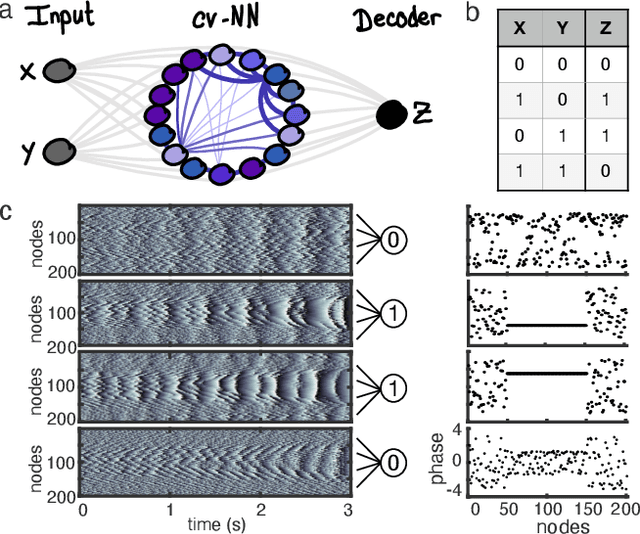
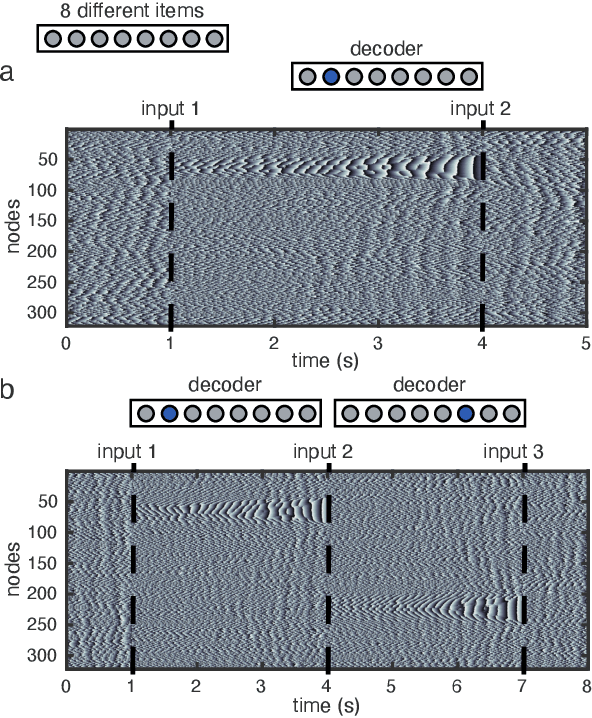
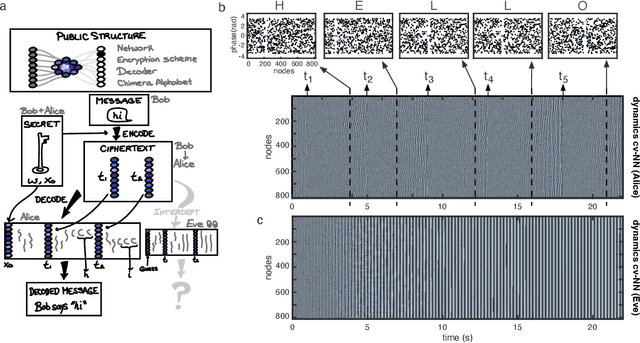
We study a complex-valued neural network (cv-NN) with linear, time-delayed interactions. We report the cv-NN displays sophisticated spatiotemporal dynamics, including partially synchronized ``chimera'' states. We then use these spatiotemporal dynamics, in combination with a nonlinear readout, for computation. The cv-NN can instantiate dynamics-based logic gates, encode short-term memories, and mediate secure message passing through a combination of interactions and time delays. The computations in this system can be fully described in an exact, closed-form mathematical expression. Finally, using direct intracellular recordings of neurons in slices from neocortex, we demonstrate that computations in the cv-NN are decodable by living biological neurons. These results demonstrate that complex-valued linear systems can perform sophisticated computations, while also being exactly solvable. Taken together, these results open future avenues for design of highly adaptable, bio-hybrid computing systems that can interface seamlessly with other neural networks.