Kuramoto Orientation Diffusion Models

Orientation-rich images, such as fingerprints and textures, often exhibit coherent angular directional patterns that are challenging to model using standard generative approaches based on isotropic Euclidean diffusion. Motivated by the role of phase synchronization in biological systems, we propose a score-based generative model built on periodic domains by leveraging stochastic Kuramoto dynamics in the diffusion process. In neural and physical systems, Kuramoto models capture synchronization phenomena across coupled oscillators -- a behavior that we re-purpose here as an inductive bias for structured image generation. In our framework, the forward process performs \textit{synchronization} among phase variables through globally or locally coupled oscillator interactions and attraction to a global reference phase, gradually collapsing the data into a low-entropy von Mises distribution. The reverse process then performs \textit{desynchronization}, generating diverse patterns by reversing the dynamics with a learned score function. This approach enables structured destruction during forward diffusion and a hierarchical generation process that progressively refines global coherence into fine-scale details. We implement wrapped Gaussian transition kernels and periodicity-aware networks to account for the circular geometry. Our method achieves competitive results on general image benchmarks and significantly improves generation quality on orientation-dense datasets like fingerprints and textures. Ultimately, this work demonstrates the promise of biologically inspired synchronization dynamics as structured priors in generative modeling.

Langevin Flows for Modeling Neural Latent Dynamics

Neural populations exhibit latent dynamical structures that drive time-evolving spiking activities, motivating the search for models that capture both intrinsic network dynamics and external unobserved influences. In this work, we introduce LangevinFlow, a sequential Variational Auto-Encoder where the time evolution of latent variables is governed by the underdamped Langevin equation. Our approach incorporates physical priors -- such as inertia, damping, a learned potential function, and stochastic forces -- to represent both autonomous and non-autonomous processes in neural systems. Crucially, the potential function is parameterized as a network of locally coupled oscillators, biasing the model toward oscillatory and flow-like behaviors observed in biological neural populations. Our model features a recurrent encoder, a one-layer Transformer decoder, and Langevin dynamics in the latent space. Empirically, our method outperforms state-of-the-art baselines on synthetic neural populations generated by a Lorenz attractor, closely matching ground-truth firing rates. On the Neural Latents Benchmark (NLB), the model achieves superior held-out neuron likelihoods (bits per spike) and forward prediction accuracy across four challenging datasets. It also matches or surpasses alternative methods in decoding behavioral metrics such as hand velocity. Overall, this work introduces a flexible, physics-inspired, high-performing framework for modeling complex neural population dynamics and their unobserved influences.

Traveling Waves Integrate Spatial Information Into Spectral Representations

Traveling waves are widely observed in the brain, but their precise computational function remains unclear. One prominent hypothesis is that they enable the transfer and integration of spatial information across neural populations. However, few computational models have explored how traveling waves might be harnessed to perform such integrative processing. Drawing inspiration from the famous ``Can one hear the shape of a drum?'' problem -- which highlights how spectral modes encode geometric information -- we introduce a set of convolutional recurrent neural networks that learn to produce traveling waves in their hidden states in response to visual stimuli. By applying a spectral decomposition to these wave-like activations, we obtain a powerful new representational space that outperforms equivalently local feed-forward networks on tasks requiring global spatial context. In particular, we observe that traveling waves effectively expand the receptive field of locally connected neurons, supporting long-range encoding and communication of information. We demonstrate that models equipped with this mechanism and spectral readouts solve visual semantic segmentation tasks demanding global integration, where local feed-forward models fail. As a first step toward traveling-wave-based representations in artificial networks, our findings suggest potential efficiency benefits and offer a new framework for connecting to biological recordings of neural activity.

Learning Artistic Signatures: Symmetry Discovery and Style Transfer

Despite nearly a decade of literature on style transfer, there is no undisputed definition of artistic style. State-of-the-art models produce impressive results but are difficult to interpret since, without a coherent definition of style, the problem of style transfer is inherently ill-posed. Early work framed style-transfer as an optimization problem but treated style as a measure only of texture. This led to artifacts in the outputs of early models where content features from the style image sometimes bled into the output image. Conversely, more recent work with diffusion models offers compelling empirical results but provides little theoretical grounding. To address these issues, we propose an alternative definition of artistic style. We suggest that style should be thought of as a set of global symmetries that dictate the arrangement of local textures. We validate this perspective empirically by learning the symmetries of a large dataset of paintings and showing that symmetries are predictive of the artistic movement to which each painting belongs. Finally, we show that by considering both local and global features, using both Lie generators and traditional measures of texture, we can quantitatively capture the stylistic similarity between artists better than with either set of features alone. This approach not only aligns well with art historians' consensus but also offers a robust framework for distinguishing nuanced stylistic differences, allowing for a more interpretable, theoretically grounded approach to style transfer.

Deep Generative Models of Music Expectation

A prominent theory of affective response to music revolves around the concepts of surprisal and expectation. In prior work, this idea has been operationalized in the form of probabilistic models of music which allow for precise computation of song (or note-by-note) probabilities, conditioned on a 'training set' of prior musical or cultural experiences. To date, however, these models have been limited to compute exact probabilities through hand-crafted features or restricted to linear models which are likely not sufficient to represent the complex conditional distributions present in music. In this work, we propose to use modern deep probabilistic generative models in the form of a Diffusion Model to compute an approximate likelihood of a musical input sequence. Unlike prior work, such a generative model parameterized by deep neural networks is able to learn complex non-linear features directly from a training set itself. In doing so, we expect to find that such models are able to more accurately represent the 'surprisal' of music for human listeners. From the literature, it is known that there is an inverted U-shaped relationship between surprisal and the amount human subjects 'like' a given song. In this work we show that pre-trained diffusion models indeed yield musical surprisal values which exhibit a negative quadratic relationship with measured subject 'liking' ratings, and that the quality of this relationship is competitive with state of the art methods such as IDyOM. We therefore present this model a preliminary step in developing modern deep generative models of music expectation and subjective likability.

Flow Factorized Representation Learning

A prominent goal of representation learning research is to achieve representations which are factorized in a useful manner with respect to the ground truth factors of variation. The fields of disentangled and equivariant representation learning have approached this ideal from a range of complimentary perspectives; however, to date, most approaches have proven to either be ill-specified or insufficiently flexible to effectively separate all realistic factors of interest in a learned latent space. In this work, we propose an alternative viewpoint on such structured representation learning which we call Flow Factorized Representation Learning, and demonstrate it to learn both more efficient and more usefully structured representations than existing frameworks. Specifically, we introduce a generative model which specifies a distinct set of latent probability paths that define different input transformations. Each latent flow is generated by the gradient field of a learned potential following dynamic optimal transport. Our novel setup brings new understandings to both \textit{disentanglement} and \textit{equivariance}. We show that our model achieves higher likelihoods on standard representation learning benchmarks while simultaneously being closer to approximately equivariant models. Furthermore, we demonstrate that the transformations learned by our model are flexibly composable and can also extrapolate to new data, implying a degree of robustness and generalizability approaching the ultimate goal of usefully factorized representation learning.

Traveling Waves Encode the Recent Past and Enhance Sequence Learning

Traveling waves of neural activity have been observed throughout the brain at a diversity of regions and scales; however, their precise computational role is still debated. One physically grounded hypothesis suggests that the cortical sheet may act like a wave-field capable of storing a short-term memory of sequential stimuli through induced waves traveling across the cortical surface. To date, however, the computational implications of this idea have remained hypothetical due to the lack of a simple recurrent neural network architecture capable of exhibiting such waves. In this work, we introduce a model to fill this gap, which we denote the Wave-RNN (wRNN), and demonstrate how both connectivity constraints and initialization play a crucial role in the emergence of wave-like dynamics. We then empirically show how such an architecture indeed efficiently encodes the recent past through a suite of synthetic memory tasks where wRNNs learn faster and perform significantly better than wave-free counterparts. Finally, we explore the implications of this memory storage system on more complex sequence modeling tasks such as sequential image classification and find that wave-based models not only again outperform comparable wave-free RNNs while using significantly fewer parameters, but additionally perform comparably to more complex gated architectures such as LSTMs and GRUs. We conclude with a discussion of the implications of these results for both neuroscience and machine learning.

DUET: 2D Structured and Approximately Equivariant Representations

Multiview Self-Supervised Learning (MSSL) is based on learning invariances with respect to a set of input transformations. However, invariance partially or totally removes transformation-related information from the representations, which might harm performance for specific downstream tasks that require such information. We propose 2D strUctured and EquivarianT representations (coined DUET), which are 2d representations organized in a matrix structure, and equivariant with respect to transformations acting on the input data. DUET representations maintain information about an input transformation, while remaining semantically expressive. Compared to SimCLR (Chen et al., 2020) (unstructured and invariant) and ESSL (Dangovski et al., 2022) (unstructured and equivariant), the structured and equivariant nature of DUET representations enables controlled generation with lower reconstruction error, while controllability is not possible with SimCLR or ESSL. DUET also achieves higher accuracy for several discriminative tasks, and improves transfer learning.

Homomorphic Self-Supervised Learning

In this work, we observe that many existing self-supervised learning algorithms can be both unified and generalized when seen through the lens of equivariant representations. Specifically, we introduce a general framework we call Homomorphic Self-Supervised Learning, and theoretically show how it may subsume the use of input-augmentations provided an augmentation-homomorphic feature extractor. We validate this theory experimentally for simple augmentations, demonstrate how the framework fails when representational structure is removed, and further empirically explore how the parameters of this framework relate to those of traditional augmentation-based self-supervised learning. We conclude with a discussion of the potential benefits afforded by this new perspective on self-supervised learning.

Modeling Category-Selective Cortical Regions with Topographic Variational Autoencoders

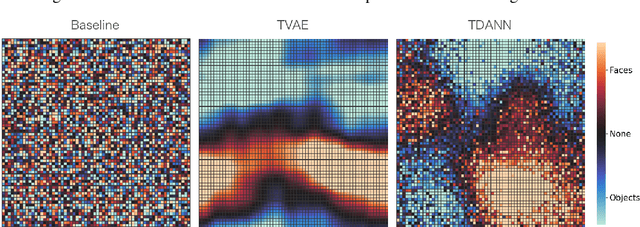
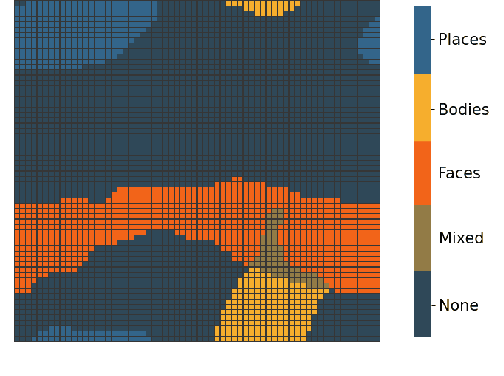
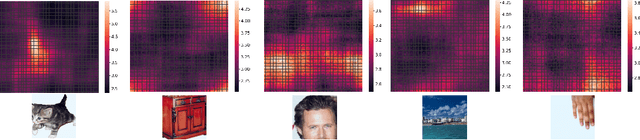
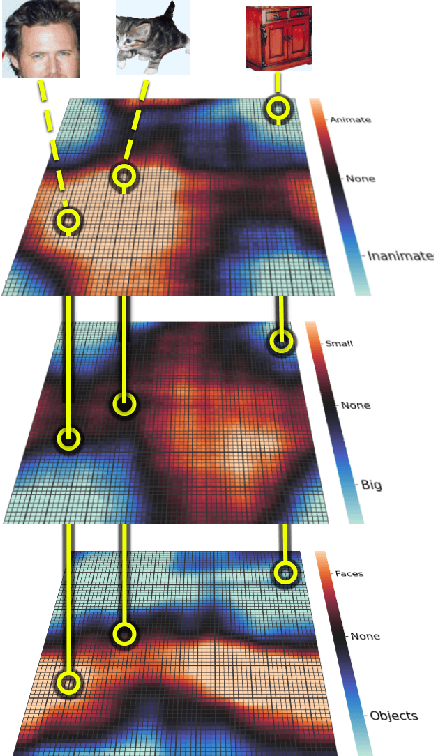
Category-selectivity in the brain describes the observation that certain spatially localized areas of the cerebral cortex tend to respond robustly and selectively to stimuli from specific limited categories. One of the most well known examples of category-selectivity is the Fusiform Face Area (FFA), an area of the inferior temporal cortex in primates which responds preferentially to images of faces when compared with objects or other generic stimuli. In this work, we leverage the newly introduced Topographic Variational Autoencoder to model of the emergence of such localized category-selectivity in an unsupervised manner. Experimentally, we demonstrate our model yields spatially dense neural clusters selective to faces, bodies, and places through visualized maps of Cohen's d metric. We compare our model with related supervised approaches, namely the TDANN, and discuss both theoretical and empirical similarities. Finally, we show preliminary results suggesting that our model yields a nested spatial hierarchy of increasingly abstract categories, analogous to observations from the human ventral temporal cortex.