Data-driven solar forecasting enables near-optimal economic decisions

Solar energy adoption is critical to achieving net-zero emissions. However, it remains difficult for many industrial and commercial actors to decide on whether they should adopt distributed solar-battery systems, which is largely due to the unavailability of fast, low-cost, and high-resolution irradiance forecasts. Here, we present SunCastNet, a lightweight data-driven forecasting system that provides 0.05$^\circ$, 10-minute resolution predictions of surface solar radiation downwards (SSRD) up to 7 days ahead. SunCastNet, coupled with reinforcement learning (RL) for battery scheduling, reduces operational regret by 76--93\% compared to robust decision making (RDM). In 25-year investment backtests, it enables up to five of ten high-emitting industrial sectors per region to cross the commercial viability threshold of 12\% Internal Rate of Return (IRR). These results show that high-resolution, long-horizon solar forecasts can directly translate into measurable economic gains, supporting near-optimal energy operations and accelerating renewable deployment.

OneRec-V2 Technical Report

Recent breakthroughs in generative AI have transformed recommender systems through end-to-end generation. OneRec reformulates recommendation as an autoregressive generation task, achieving high Model FLOPs Utilization. While OneRec-V1 has shown significant empirical success in real-world deployment, two critical challenges hinder its scalability and performance: (1) inefficient computational allocation where 97.66% of resources are consumed by sequence encoding rather than generation, and (2) limitations in reinforcement learning relying solely on reward models. To address these challenges, we propose OneRec-V2, featuring: (1) Lazy Decoder-Only Architecture: Eliminates encoder bottlenecks, reducing total computation by 94% and training resources by 90%, enabling successful scaling to 8B parameters. (2) Preference Alignment with Real-World User Interactions: Incorporates Duration-Aware Reward Shaping and Adaptive Ratio Clipping to better align with user preferences using real-world feedback. Extensive A/B tests on Kuaishou demonstrate OneRec-V2's effectiveness, improving App Stay Time by 0.467%/0.741% while balancing multi-objective recommendations. This work advances generative recommendation scalability and alignment with real-world feedback, representing a step forward in the development of end-to-end recommender systems.

Langevin Flows for Modeling Neural Latent Dynamics

Neural populations exhibit latent dynamical structures that drive time-evolving spiking activities, motivating the search for models that capture both intrinsic network dynamics and external unobserved influences. In this work, we introduce LangevinFlow, a sequential Variational Auto-Encoder where the time evolution of latent variables is governed by the underdamped Langevin equation. Our approach incorporates physical priors -- such as inertia, damping, a learned potential function, and stochastic forces -- to represent both autonomous and non-autonomous processes in neural systems. Crucially, the potential function is parameterized as a network of locally coupled oscillators, biasing the model toward oscillatory and flow-like behaviors observed in biological neural populations. Our model features a recurrent encoder, a one-layer Transformer decoder, and Langevin dynamics in the latent space. Empirically, our method outperforms state-of-the-art baselines on synthetic neural populations generated by a Lorenz attractor, closely matching ground-truth firing rates. On the Neural Latents Benchmark (NLB), the model achieves superior held-out neuron likelihoods (bits per spike) and forward prediction accuracy across four challenging datasets. It also matches or surpasses alternative methods in decoding behavioral metrics such as hand velocity. Overall, this work introduces a flexible, physics-inspired, high-performing framework for modeling complex neural population dynamics and their unobserved influences.

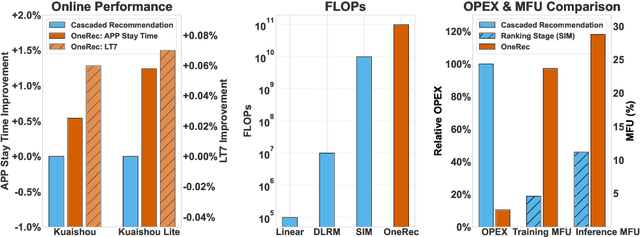
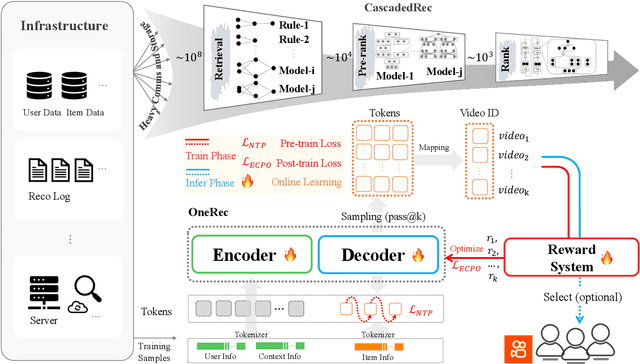
OneRec Technical Report

Recommender systems have been widely used in various large-scale user-oriented platforms for many years. However, compared to the rapid developments in the AI community, recommendation systems have not achieved a breakthrough in recent years. For instance, they still rely on a multi-stage cascaded architecture rather than an end-to-end approach, leading to computational fragmentation and optimization inconsistencies, and hindering the effective application of key breakthrough technologies from the AI community in recommendation scenarios. To address these issues, we propose OneRec, which reshapes the recommendation system through an end-to-end generative approach and achieves promising results. Firstly, we have enhanced the computational FLOPs of the current recommendation model by 10 $\times$ and have identified the scaling laws for recommendations within certain boundaries. Secondly, reinforcement learning techniques, previously difficult to apply for optimizing recommendations, show significant potential in this framework. Lastly, through infrastructure optimizations, we have achieved 23.7% and 28.8% Model FLOPs Utilization (MFU) on flagship GPUs during training and inference, respectively, aligning closely with the LLM community. This architecture significantly reduces communication and storage overhead, resulting in operating expense that is only 10.6% of traditional recommendation pipelines. Deployed in Kuaishou/Kuaishou Lite APP, it handles 25% of total queries per second, enhancing overall App Stay Time by 0.54% and 1.24%, respectively. Additionally, we have observed significant increases in metrics such as 7-day Lifetime, which is a crucial indicator of recommendation experience. We also provide practical lessons and insights derived from developing, optimizing, and maintaining a production-scale recommendation system with significant real-world impact.

Is CLIP ideal? No. Can we fix it? Yes!

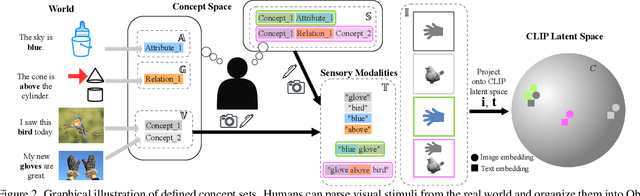
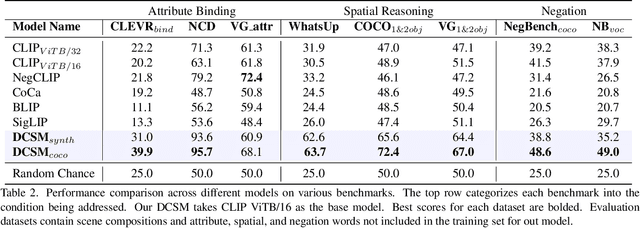
Contrastive Language-Image Pre-Training (CLIP) is a popular method for learning multimodal latent spaces with well-organized semantics. Despite its wide range of applications, CLIP's latent space is known to fail at handling complex visual-textual interactions. Recent works attempt to address its shortcomings with data-centric or algorithmic approaches. But what if the problem is more fundamental, and lies in the geometry of CLIP? Toward this end, we rigorously analyze CLIP's latent space properties, and prove that no CLIP-like joint embedding space exists which can correctly do any two of the following at the same time: 1. represent basic descriptions and image content, 2. represent attribute binding, 3. represent spatial location and relationships, 4. represent negation. Informed by this analysis, we propose Dense Cosine Similarity Maps (DCSMs) as a principled and interpretable scoring method for CLIP-like models, which solves the fundamental limitations of CLIP by retaining the semantic topology of the image patches and text tokens. This method improves upon the performance of classical CLIP-like joint encoder models on a wide array of benchmarks. We share our code and data here for reproducibility: https://github.com/Raphoo/DCSM_Ideal_CLIP

Unsupervised Region-Based Image Editing of Denoising Diffusion Models

Although diffusion models have achieved remarkable success in the field of image generation, their latent space remains under-explored. Current methods for identifying semantics within latent space often rely on external supervision, such as textual information and segmentation masks. In this paper, we propose a method to identify semantic attributes in the latent space of pre-trained diffusion models without any further training. By projecting the Jacobian of the targeted semantic region into a low-dimensional subspace which is orthogonal to the non-masked regions, our approach facilitates precise semantic discovery and control over local masked areas, eliminating the need for annotations. We conducted extensive experiments across multiple datasets and various architectures of diffusion models, achieving state-of-the-art performance. In particular, for some specific face attributes, the performance of our proposed method even surpasses that of supervised approaches, demonstrating its superior ability in editing local image properties.

Morphological-Symmetry-Equivariant Heterogeneous Graph Neural Network for Robotic Dynamics Learning

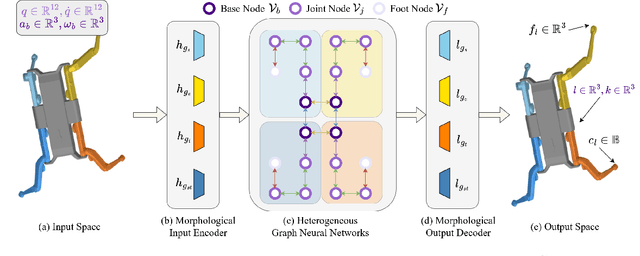
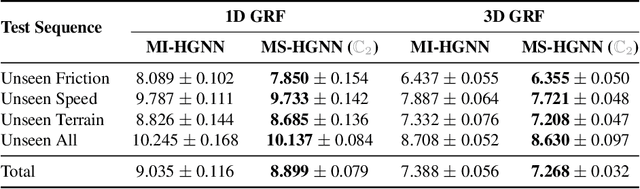
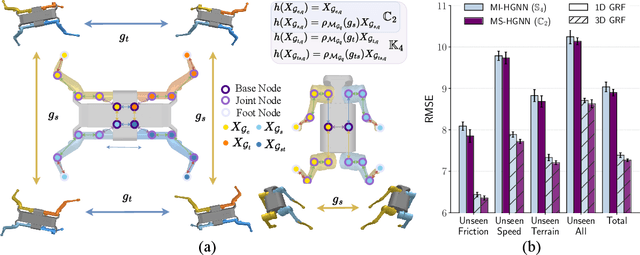
We present a morphological-symmetry-equivariant heterogeneous graph neural network, namely MS-HGNN, for robotic dynamics learning, that integrates robotic kinematic structures and morphological symmetries into a single graph network. These structural priors are embedded into the learning architecture as constraints, ensuring high generalizability, sample and model efficiency. The proposed MS-HGNN is a versatile and general architecture that is applicable to various multi-body dynamic systems and a wide range of dynamics learning problems. We formally prove the morphological-symmetry-equivariant property of our MS-HGNN and validate its effectiveness across multiple quadruped robot learning problems using both real-world and simulated data. Our code is made publicly available at https://github.com/lunarlab-gatech/MorphSym-HGNN/.

RMLR: Extending Multinomial Logistic Regression into General Geometries

Riemannian neural networks, which extend deep learning techniques to Riemannian spaces, have gained significant attention in machine learning. To better classify the manifold-valued features, researchers have started extending Euclidean multinomial logistic regression (MLR) into Riemannian manifolds. However, existing approaches suffer from limited applicability due to their strong reliance on specific geometric properties. This paper proposes a framework for designing Riemannian MLR over general geometries, referred to as RMLR. Our framework only requires minimal geometric properties, thus exhibiting broad applicability and enabling its use with a wide range of geometries. Specifically, we showcase our framework on the Symmetric Positive Definite (SPD) manifold and special orthogonal group, i.e., the set of rotation matrices. On the SPD manifold, we develop five families of SPD MLRs under five types of power-deformed metrics. On rotation matrices we propose Lie MLR based on the popular bi-invariant metric. Extensive experiments on different Riemannian backbone networks validate the effectiveness of our framework.

Understanding Matrix Function Normalizations in Covariance Pooling through the Lens of Riemannian Geometry

Global Covariance Pooling (GCP) has been demonstrated to improve the performance of Deep Neural Networks (DNNs) by exploiting second-order statistics of high-level representations. GCP typically performs classification of the covariance matrices by applying matrix function normalization, such as matrix logarithm or power, followed by a Euclidean classifier. However, covariance matrices inherently lie in a Riemannian manifold, known as the Symmetric Positive Definite (SPD) manifold. The current literature does not provide a satisfactory explanation of why Euclidean classifiers can be applied directly to Riemannian features after the normalization of the matrix power. To mitigate this gap, this paper provides a comprehensive and unified understanding of the matrix logarithm and power from a Riemannian geometry perspective. The underlying mechanism of matrix functions in GCP is interpreted from two perspectives: one based on tangent classifiers (Euclidean classifiers on the tangent space) and the other based on Riemannian classifiers. Via theoretical analysis and empirical validation through extensive experiments on fine-grained and large-scale visual classification datasets, we conclude that the working mechanism of the matrix functions should be attributed to the Riemannian classifiers they implicitly respect.

Product Geometries on Cholesky Manifolds with Applications to SPD Manifolds

This paper presents two new metrics on the Symmetric Positive Definite (SPD) manifold via the Cholesky manifold, i.e., the space of lower triangular matrices with positive diagonal elements. We first unveil that the existing popular Riemannian metric on the Cholesky manifold can be generally characterized as the product metric of a Euclidean metric and a Riemannian metric on the space of n-dimensional positive vectors. Based on this analysis, we propose two novel metrics on the Cholesky manifolds, i.e., Diagonal Power Euclidean Metric and Diagonal Generalized Bures-Wasserstein Metric, which are numerically stabler than the existing Cholesky metric. We also discuss the gyro structures and deformed metrics associated with our metrics. The gyro structures connect the linear and geometric properties, while the deformed metrics interpolate between our proposed metrics and the existing metric. Further, by Cholesky decomposition, the proposed deformed metrics and gyro structures are pulled back to SPD manifolds. Compared with existing Riemannian metrics on SPD manifolds, our metrics are easy to use, computationally efficient, and numerically stable.