MeSH: Memory-as-State-Highways for Recursive Transformers

Recursive transformers reuse parameters and iterate over hidden states multiple times, decoupling compute depth from parameter depth. However, under matched compute, recursive models with fewer parameters often lag behind non-recursive counterparts. By probing hidden states, we trace this performance gap to two primary bottlenecks: undifferentiated computation, where the core is forced to adopt a similar computational pattern at every iteration, and information overload, where long-lived and transient information must coexist in a single hidden state. To address the issues, we introduce a Memory-as-State-Highways (MeSH) scheme, which externalizes state management into an explicit memory buffer and employs lightweight routers to dynamically diversify computation across iterations. Probing visualizations confirm that MeSH successfully resolves the pathologies by inducing functional specialization across iterations. On the Pythia suite (160M-1.4B), MeSH-enhanced recursive transformers consistently improve over recursive baselines and outperforms its larger non-recursive counterpart at the 1.4B scale, improving average downstream accuracy by +1.06% with 33% fewer non-embedding parameters. Our analysis establishes MeSH as a scalable and principled architecture for building stronger recursive models.

Riemannian Batch Normalization: A Gyro Approach

Normalization layers are crucial for deep learning, but their Euclidean formulations are inadequate for data on manifolds. On the other hand, many Riemannian manifolds in machine learning admit gyro-structures, enabling principled extensions of Euclidean neural networks to non-Euclidean domains. Inspired by this, we introduce GyroBN, a principled Riemannian batch normalization framework for gyrogroups. We establish two necessary conditions, namely \emph{pseudo-reduction} and \emph{gyroisometric gyrations}, that guarantee GyroBN with theoretical control over sample statistics, and show that these conditions hold for all known gyrogroups in machine learning. Our framework also incorporates several existing Riemannian normalization methods as special cases. We further instantiate GyroBN on seven representative geometries, including the Grassmannian, five constant curvature spaces, and the correlation manifold, and derive novel gyro and Riemannian structures to enable these instantiations. Experiments across these geometries demonstrate the effectiveness of GyroBN. The code is available at https://github.com/GitZH-Chen/GyroBN.git.

FUTURE: Flexible Unlearning for Tree Ensemble

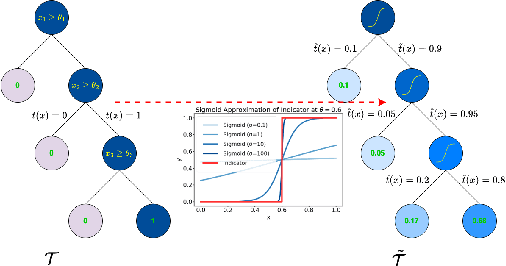
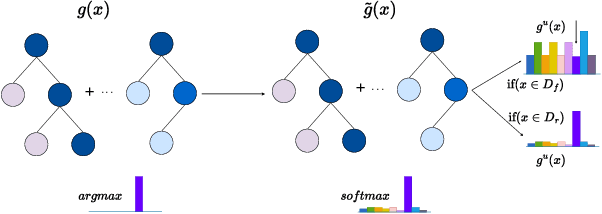
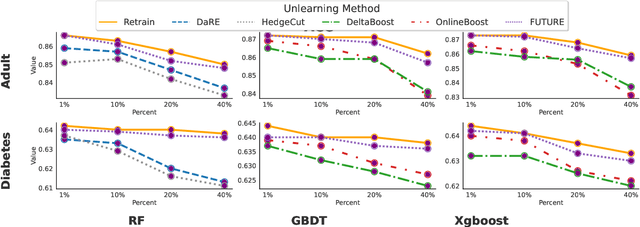
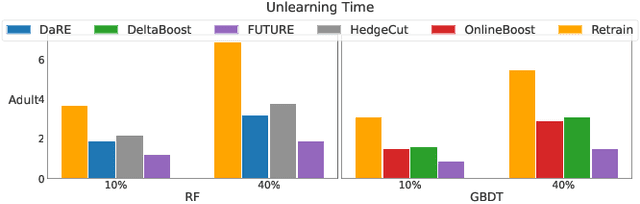
Tree ensembles are widely recognized for their effectiveness in classification tasks, achieving state-of-the-art performance across diverse domains, including bioinformatics, finance, and medical diagnosis. With increasing emphasis on data privacy and the \textit{right to be forgotten}, several unlearning algorithms have been proposed to enable tree ensembles to forget sensitive information. However, existing methods are often tailored to a particular model or rely on the discrete tree structure, making them difficult to generalize to complex ensembles and inefficient for large-scale datasets. To address these limitations, we propose FUTURE, a novel unlearning algorithm for tree ensembles. Specifically, we formulate the problem of forgetting samples as a gradient-based optimization task. In order to accommodate non-differentiability of tree ensembles, we adopt the probabilistic model approximations within the optimization framework. This enables end-to-end unlearning in an effective and efficient manner. Extensive experiments on real-world datasets show that FUTURE yields significant and successful unlearning performance.

Learning to Normalize on the SPD Manifold under Bures-Wasserstein Geometry

Covariance matrices have proven highly effective across many scientific fields. Since these matrices lie within the Symmetric Positive Definite (SPD) manifold - a Riemannian space with intrinsic non-Euclidean geometry, the primary challenge in representation learning is to respect this underlying geometric structure. Drawing inspiration from the success of Euclidean deep learning, researchers have developed neural networks on the SPD manifolds for more faithful covariance embedding learning. A notable advancement in this area is the implementation of Riemannian batch normalization (RBN), which has been shown to improve the performance of SPD network models. Nonetheless, the Riemannian metric beneath the existing RBN might fail to effectively deal with the ill-conditioned SPD matrices (ICSM), undermining the effectiveness of RBN. In contrast, the Bures-Wasserstein metric (BWM) demonstrates superior performance for ill-conditioning. In addition, the recently introduced Generalized BWM (GBWM) parameterizes the vanilla BWM via an SPD matrix, allowing for a more nuanced representation of vibrant geometries of the SPD manifold. Therefore, we propose a novel RBN algorithm based on the GBW geometry, incorporating a learnable metric parameter. Moreover, the deformation of GBWM by matrix power is also introduced to further enhance the representational capacity of GBWM-based RBN. Experimental results on different datasets validate the effectiveness of our proposed method.

Characterizing GPU Resilience and Impact on AI/HPC Systems

In this study, we characterize GPU failures in Delta, the current large-scale AI system with over 600 petaflops of peak compute throughput. The system comprises GPU and non-GPU nodes with modern AI accelerators, such as NVIDIA A40, A100, and H100 GPUs. The study uses two and a half years of data on GPU errors. We evaluate the resilience of GPU hardware components to determine the vulnerability of different GPU components to failure and their impact on the GPU and node availability. We measure the key propagation paths in GPU hardware, GPU interconnect (NVLink), and GPU memory. Finally, we evaluate the impact of the observed GPU errors on user jobs. Our key findings are: (i) Contrary to common beliefs, GPU memory is over 30x more reliable than GPU hardware in terms of MTBE (mean time between errors). (ii) The newly introduced GSP (GPU System Processor) is the most vulnerable GPU hardware component. (iii) NVLink errors did not always lead to user job failure, and we attribute it to the underlying error detection and retry mechanisms employed. (iv) We show multiple examples of hardware errors originating from one of the key GPU hardware components, leading to application failure. (v) We project the impact of GPU node availability on larger scales with emulation and find that significant overprovisioning between 5-20% would be necessary to handle GPU failures. If GPU availability were improved to 99.9%, the overprovisioning would be reduced by 4x.

RMLR: Extending Multinomial Logistic Regression into General Geometries

Riemannian neural networks, which extend deep learning techniques to Riemannian spaces, have gained significant attention in machine learning. To better classify the manifold-valued features, researchers have started extending Euclidean multinomial logistic regression (MLR) into Riemannian manifolds. However, existing approaches suffer from limited applicability due to their strong reliance on specific geometric properties. This paper proposes a framework for designing Riemannian MLR over general geometries, referred to as RMLR. Our framework only requires minimal geometric properties, thus exhibiting broad applicability and enabling its use with a wide range of geometries. Specifically, we showcase our framework on the Symmetric Positive Definite (SPD) manifold and special orthogonal group, i.e., the set of rotation matrices. On the SPD manifold, we develop five families of SPD MLRs under five types of power-deformed metrics. On rotation matrices we propose Lie MLR based on the popular bi-invariant metric. Extensive experiments on different Riemannian backbone networks validate the effectiveness of our framework.

Understanding Matrix Function Normalizations in Covariance Pooling through the Lens of Riemannian Geometry

Global Covariance Pooling (GCP) has been demonstrated to improve the performance of Deep Neural Networks (DNNs) by exploiting second-order statistics of high-level representations. GCP typically performs classification of the covariance matrices by applying matrix function normalization, such as matrix logarithm or power, followed by a Euclidean classifier. However, covariance matrices inherently lie in a Riemannian manifold, known as the Symmetric Positive Definite (SPD) manifold. The current literature does not provide a satisfactory explanation of why Euclidean classifiers can be applied directly to Riemannian features after the normalization of the matrix power. To mitigate this gap, this paper provides a comprehensive and unified understanding of the matrix logarithm and power from a Riemannian geometry perspective. The underlying mechanism of matrix functions in GCP is interpreted from two perspectives: one based on tangent classifiers (Euclidean classifiers on the tangent space) and the other based on Riemannian classifiers. Via theoretical analysis and empirical validation through extensive experiments on fine-grained and large-scale visual classification datasets, we conclude that the working mechanism of the matrix functions should be attributed to the Riemannian classifiers they implicitly respect.

Product Geometries on Cholesky Manifolds with Applications to SPD Manifolds

This paper presents two new metrics on the Symmetric Positive Definite (SPD) manifold via the Cholesky manifold, i.e., the space of lower triangular matrices with positive diagonal elements. We first unveil that the existing popular Riemannian metric on the Cholesky manifold can be generally characterized as the product metric of a Euclidean metric and a Riemannian metric on the space of n-dimensional positive vectors. Based on this analysis, we propose two novel metrics on the Cholesky manifolds, i.e., Diagonal Power Euclidean Metric and Diagonal Generalized Bures-Wasserstein Metric, which are numerically stabler than the existing Cholesky metric. We also discuss the gyro structures and deformed metrics associated with our metrics. The gyro structures connect the linear and geometric properties, while the deformed metrics interpolate between our proposed metrics and the existing metric. Further, by Cholesky decomposition, the proposed deformed metrics and gyro structures are pulled back to SPD manifolds. Compared with existing Riemannian metrics on SPD manifolds, our metrics are easy to use, computationally efficient, and numerically stable.

Debiasing Machine Unlearning with Counterfactual Examples

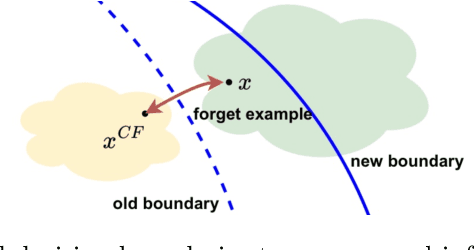
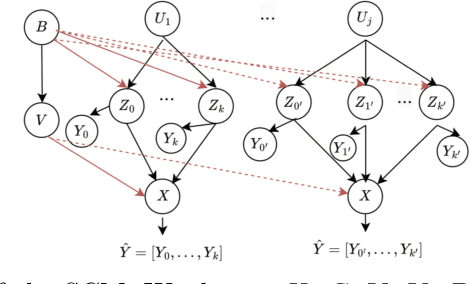
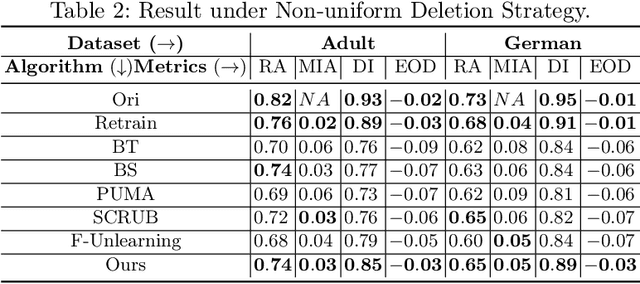
The right to be forgotten (RTBF) seeks to safeguard individuals from the enduring effects of their historical actions by implementing machine-learning techniques. These techniques facilitate the deletion of previously acquired knowledge without requiring extensive model retraining. However, they often overlook a critical issue: unlearning processes bias. This bias emerges from two main sources: (1) data-level bias, characterized by uneven data removal, and (2) algorithm-level bias, which leads to the contamination of the remaining dataset, thereby degrading model accuracy. In this work, we analyze the causal factors behind the unlearning process and mitigate biases at both data and algorithmic levels. Typically, we introduce an intervention-based approach, where knowledge to forget is erased with a debiased dataset. Besides, we guide the forgetting procedure by leveraging counterfactual examples, as they maintain semantic data consistency without hurting performance on the remaining dataset. Experimental results demonstrate that our method outperforms existing machine unlearning baselines on evaluation metrics.

A Lie Group Approach to Riemannian Batch Normalization

Manifold-valued measurements exist in numerous applications within computer vision and machine learning. Recent studies have extended Deep Neural Networks (DNNs) to manifolds, and concomitantly, normalization techniques have also been adapted to several manifolds, referred to as Riemannian normalization. Nonetheless, most of the existing Riemannian normalization methods have been derived in an ad hoc manner and only apply to specific manifolds. This paper establishes a unified framework for Riemannian Batch Normalization (RBN) techniques on Lie groups. Our framework offers the theoretical guarantee of controlling both the Riemannian mean and variance. Empirically, we focus on Symmetric Positive Definite (SPD) manifolds, which possess three distinct types of Lie group structures. Using the deformation concept, we generalize the existing Lie groups on SPD manifolds into three families of parameterized Lie groups. Specific normalization layers induced by these Lie groups are then proposed for SPD neural networks. We demonstrate the effectiveness of our approach through three sets of experiments: radar recognition, human action recognition, and electroencephalography (EEG) classification. The code is available at https://github.com/GitZH-Chen/LieBN.git.