Learning Artistic Signatures: Symmetry Discovery and Style Transfer

Despite nearly a decade of literature on style transfer, there is no undisputed definition of artistic style. State-of-the-art models produce impressive results but are difficult to interpret since, without a coherent definition of style, the problem of style transfer is inherently ill-posed. Early work framed style-transfer as an optimization problem but treated style as a measure only of texture. This led to artifacts in the outputs of early models where content features from the style image sometimes bled into the output image. Conversely, more recent work with diffusion models offers compelling empirical results but provides little theoretical grounding. To address these issues, we propose an alternative definition of artistic style. We suggest that style should be thought of as a set of global symmetries that dictate the arrangement of local textures. We validate this perspective empirically by learning the symmetries of a large dataset of paintings and showing that symmetries are predictive of the artistic movement to which each painting belongs. Finally, we show that by considering both local and global features, using both Lie generators and traditional measures of texture, we can quantitatively capture the stylistic similarity between artists better than with either set of features alone. This approach not only aligns well with art historians' consensus but also offers a robust framework for distinguishing nuanced stylistic differences, allowing for a more interpretable, theoretically grounded approach to style transfer.

Matrix Factorization in Tropical and Mixed Tropical-Linear Algebras

Matrix Factorization (MF) has found numerous applications in Machine Learning and Data Mining, including collaborative filtering recommendation systems, dimensionality reduction, data visualization, and community detection. Motivated by the recent successes of tropical algebra and geometry in machine learning, we investigate two problems involving matrix factorization over the tropical algebra. For the first problem, Tropical Matrix Factorization (TMF), which has been studied already in the literature, we propose an improved algorithm that avoids many of the local optima. The second formulation considers the approximate decomposition of a given matrix into the product of three matrices where a usual matrix product is followed by a tropical product. This formulation has a very interesting interpretation in terms of the learning of the utility functions of multiple users. We also present numerical results illustrating the effectiveness of the proposed algorithms, as well as an application to recommendation systems with promising results.

Learning Linear Groups in Neural Networks

Employing equivariance in neural networks leads to greater parameter efficiency and improved generalization performance through the encoding of domain knowledge in the architecture; however, the majority of existing approaches require an a priori specification of the desired symmetries. We present a neural network architecture, Linear Group Networks (LGNs), for learning linear groups acting on the weight space of neural networks. Linear groups are desirable due to their inherent interpretability, as they can be represented as finite matrices. LGNs learn groups without any supervision or knowledge of the hidden symmetries in the data and the groups can be mapped to well known operations in machine learning. We use LGNs to learn groups on multiple datasets while considering different downstream tasks; we demonstrate that the linear group structure depends on both the data distribution and the considered task.

Learning unfolded networks with a cyclic group structure

Deep neural networks lack straightforward ways to incorporate domain knowledge and are notoriously considered black boxes. Prior works attempted to inject domain knowledge into architectures implicitly through data augmentation. Building on recent advances on equivariant neural networks, we propose networks that explicitly encode domain knowledge, specifically equivariance with respect to rotations. By using unfolded architectures, a rich framework that originated from sparse coding and has theoretical guarantees, we present interpretable networks with sparse activations. The equivariant unfolded networks compete favorably with baselines, with only a fraction of their parameters, as showcased on (rotated) MNIST and CIFAR-10.

On the convergence of group-sparse autoencoders

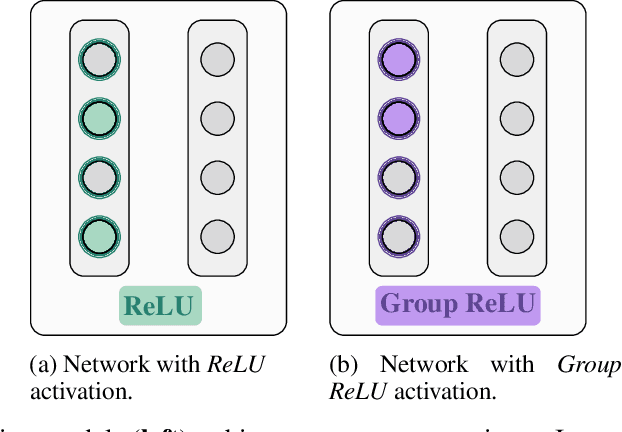
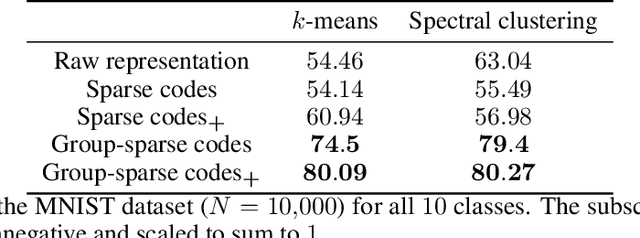
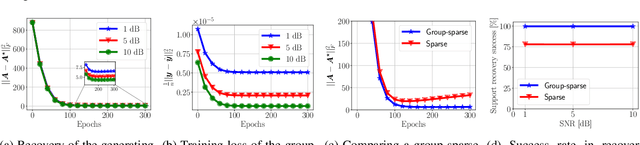
Recent approaches in the theoretical analysis of model-based deep learning architectures have studied the convergence of gradient descent in shallow ReLU networks that arise from generative models whose hidden layers are sparse. Motivated by the success of architectures that impose structured forms of sparsity, we introduce and study a group-sparse autoencoder that accounts for a variety of generative models, and utilizes a group-sparse ReLU activation function to force the non-zero units at a given layer to occur in blocks. For clustering models, inputs that result in the same group of active units belong to the same cluster. We proceed to analyze the gradient dynamics of a shallow instance of the proposed autoencoder, trained with data adhering to a group-sparse generative model. In this setting, we theoretically prove the convergence of the network parameters to a neighborhood of the generating matrix. We validate our model through numerical analysis and highlight the superior performance of networks with a group-sparse ReLU compared to networks that utilize traditional ReLUs, both in sparse coding and in parameter recovery tasks. We also provide real data experiments to corroborate the simulated results, and emphasize the clustering capabilities of structured sparsity models.

Dense and Sparse Coding: Theory and Architectures

The sparse representation model has been successfully utilized in a number of signal and image processing tasks; however, recent research has highlighted its limitations in certain deep-learning architectures. This paper proposes a novel dense and sparse coding model that considers the problem of recovering a dense vector $\mathbf{x}$ and a sparse vector $\mathbf{u}$ given linear measurements of the form $\mathbf{y} = \mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}$. Our first theoretical result proposes a new natural geometric condition based on the minimal angle between subspaces corresponding to the measurement matrices $\mathbf{A}$ and $\mathbf{B}$ to establish the uniqueness of solutions to the linear system. The second analysis shows that, under mild assumptions and sufficient linear measurements, a convex program recovers the dense and sparse components with high probability. The standard RIPless analysis cannot be directly applied to this setup. Our proof is a non-trivial adaptation of techniques from anisotropic compressive sensing theory and is based on an analysis of a matrix derived from the measurement matrices $\mathbf{A}$ and $\mathbf{B}$. We begin by demonstrating the effectiveness of the proposed model on simulated data. Then, to address its use in a dictionary learning setting, we propose a dense and sparse auto-encoder (DenSaE) that is tailored to it. We demonstrate that a) DenSaE denoises natural images better than architectures derived from the sparse coding model ($\mathbf{B}\mathbf{u}$), b) training the biases in the latter amounts to implicitly learning the $\mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{u}$ model, and c) $\mathbf{A}$ and $\mathbf{B}$ capture low- and high-frequency contents, respectively.

Tropical Geometry and Piecewise-Linear Approximation of Curves and Surfaces on Weighted Lattices

Tropical Geometry and Mathematical Morphology share the same max-plus and min-plus semiring arithmetic and matrix algebra. In this chapter we summarize some of their main ideas and common (geometric and algebraic) structure, generalize and extend both of them using weighted lattices and a max-$\star$ algebra with an arbitrary binary operation $\star$ that distributes over max, and outline applications to geometry, machine learning, and optimization. Further, we generalize tropical geometrical objects using weighted lattices. Finally, we provide the optimal solution of max-$\star$ equations using morphological adjunctions that are projections on weighted lattices, and apply it to optimal piecewise-linear regression for fitting max-$\star$ tropical curves and surfaces to arbitrary data that constitute polygonal or polyhedral shape approximations. This also includes an efficient algorithm for solving the convex regression problem of data fitting with max-affine functions.

An Adaptive Pruning Algorithm for Spoofing Localisation Based on Tropical Geometry

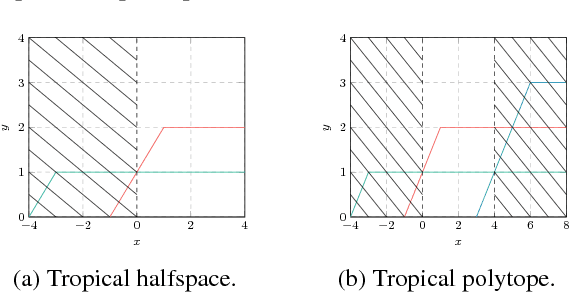
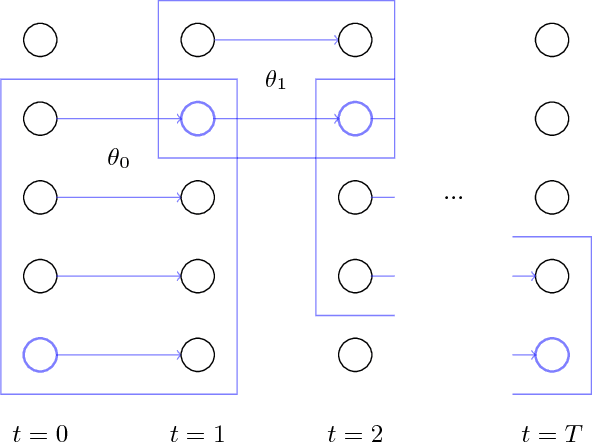
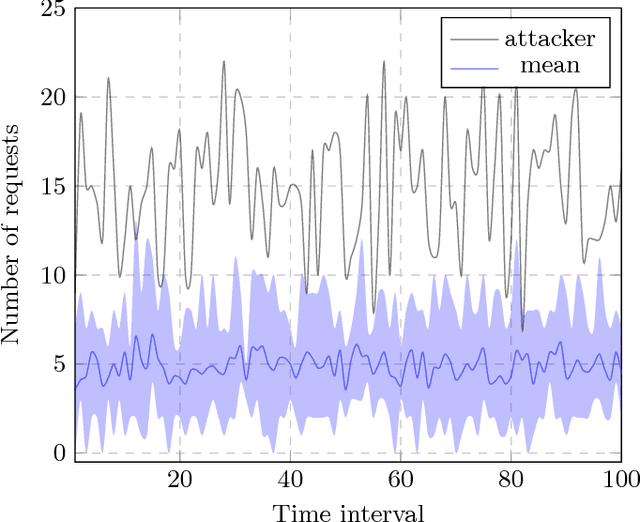
The problem of spoofing attacks is increasingly relevant as digital systems are becoming more ubiquitous. Thus the detection of such attacks and the localisation of attackers have been objects of recent study. After an attack has been detected, various algorithms have been proposed in order to localise the attacker. In this work we propose a new adaptive pruning algorithm inspired by the tropical and geometrical analysis of the traditional Viterbi pruning algorithm to solve the localisation problem. In particular, the proposed algorithm tries to localise the attacker by adapting the leniency parameter based on estimates about the state of the solution space. These estimates stem from the enclosed volume and the entropy of the solution space, as they were introduced in our previous works.

Tropical Modeling of Weighted Transducer Algorithms on Graphs

Weighted Finite State Transducers (WFSTs) are versatile data structures that can model a great number of problems, ranging from Automatic Speech Recognition to DNA sequencing. Traditional computer science algorithms are employed when working with these structures in order to optimise their size, but also the runtime of decoding algorithms. However, these algorithms are not unified under a common framework that would allow for their treatment as a whole. Moreover, the inherent geometrical representation of WFSTs, coupled with the topology-preserving algorithms that operate on them make the structures ideal for tropical analysis. The benefits of such analysis have a twofold nature; first, matrix operations offer a connection to nonlinear vector space and spectral theory, and, second, tropical algebra offers a connection to tropical geometry. In this work we model some of the most frequently used algorithms in WFSTs by using tropical algebra; this provides a theoretical unification and allows us to also analyse aspects of their tropical geometry. Further, we provide insights via numerical examples.